Multiplikativna inverzna razlaga, primeri, rešene vaje
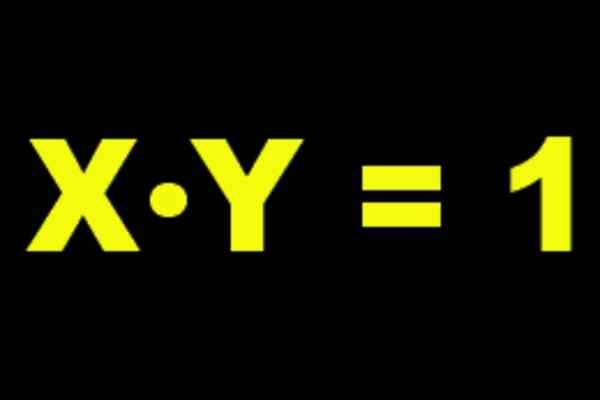
- 1480
- 335
- Raymond Moen
Razume ga Inverzno multiplikativno Od ene številke, druga številka, ki se pomnoži s prvimi rezultati v nevtralnem elementu izdelka, to pomeni, da je enota. Če imate resnično številko do potem njegovo multiplikativno inverzno označuje do-1, In izpolnjeno je:
a a-1 = a-1 A = 1
Ponavadi številka do Pripada naboru resničnih številk.
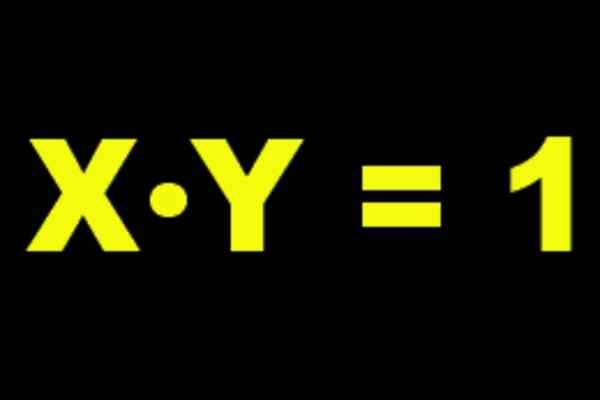 Slika 1. In je obratno mulplikativno za x in x je multiplikativno inverzno od y.
Slika 1. In je obratno mulplikativno za x in x je multiplikativno inverzno od y. Če na primer vzamemo A = 2, Potem je vaša multiplikativna inverzna 2-1 = ½ Ker je naslednje preverjeno:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Do Inverzno multiplikativno števila se imenuje tudi vzajemno, Ker se multiplikativni inverzni dobimo z izmenjavo števca in imenovalca, je na primer multiplikativni obratni 3/4 4/3.
Na splošno lahko rečemo, da za racionalno število (P/Q) Vaša multiplikativna inverzna (P/Q)-1 Je vzajemno (Q/P) Kot je mogoče preveriti spodaj:
(P/Q) ⋅ (P/Q)-1 = (p/q) ⋅ (q/p) = (p⋅ q)/(q⋅ p) = (p⋅ q)/(p⋅ q) = 1
Multiplikativni inverzni ne obstaja v numeričnem naboru celih števil, Na primer, če je vzeta celotna številka 2, bi bila njegova multiplikativna obratna glede na zgoraj navedeno ½, a ½ ni celo število.
Obstaja tudi multiplikativni inverzni element množenja. Z drugimi besedami, ničelna številka (0), ki je ničelni element množenja, nima multiplikativnega obratnega, saj ni številke, ki bi se pomnožila z ničlo enote.
Multiplikativna inverzna obstaja v racionalnih številkah, v realnih in zapletenih številkah.
Multiplikativni inverzni primeri
Primer 1
Poiščite 3/2 multiplikativno inverzno in preverite, ali izpolnjuje lastnost multiplikativnih celih števil.
Vam lahko služi: Coplanares Točke: enačba, primer in rešene vajeV skladu z zgoraj navedenim pravilom se na ta način izmenjuje multiplikativni inverzni (3/2) (2/3). Za preverjanje množenja obeh številk se izvede:
(3/2) ⋅ (2/3) = (3 ⋅ 2)/(2 ⋅ 3) = 6/6 = 1.
Če želite pomnožiti dve delni številki, preprosto pomnožite števca prvega pri drugem števcu, da pridobite števca rezultata.
Če želite pridobiti imenovalec produkta delnih številk, nadaljujte na podoben način, to je, da se imenovalci med seboj pomnožijo in rezultat je imenovalec izdelkov. V našem primeru je preverjeno, da je števca izdelka števila in njenega vzajemnega 6, imenovalec.
Primer 2
Multiplikativne inverzne -5 ne smemo zamenjati s svojim simetričnim (+5), ki se včasih imenuje aritmetična inverzna. Multiplikativni inverzni bo pridobljen na naslednji način:
(-5) ⋅ x = 1
Kjer je x multiplikativni inverzni, ki ga je treba pridobiti. Možen postopek je sestavljen iz čiščenja neznanega x. AS (-5) pomnoži neznani X v levem članu, potem se zgodi, da deli desni član:
X = 1 / (-5)
Kot je znano + med - je - potem končno dobimo x:
X = - ⅕ .
Za zaključek - ⅕ je multiplikativni inverzni.
Primer 3
Pridobite multiplikativno inverzno od -√2. Recimo, da je multiplikativni inverzni x, potem mora biti -drug pomnoženo z x enoto, stanje, ki ga nalagamo spodaj:
-√2 ⋅ x = 1
Oba člana sta razdeljena na -ploga, da dobita:
(-Drug2 ⋅ x) / (-pti
Prvi član je poenostavljen -"Preostali:
Lahko vam služi: standardna ocena napaka: kako se izračuna, primeri, vajeX = 1 / (-√2)
Ta izraz je mogoče racionalizirati, to je, da odpravimo korenino imenovalca, pomnoži v števcu (-drug) in v imenovalcu za isto količino, tako da rezultat ni spremenjen:
X = (-pti
Za zaključek - (√2/2) je multiplikativni inverzni ( -drug).
Primer 4
Predpostavite poljubno številko x, pridobite svojo multiplikativno inverzno in ga grafično predstavljajte.
V tem primeru gre za funkcijo f (x) = x, pridobitev multiplikativne inverzne je najti funkcijo g (x). Funkcija G je vzajemna funkcija F in je ne smete na noben način zamenjati s svojo obratno funkcijo.
Z drugimi besedami, multiplikativni inverzni X je a in tako, da se izpolni naslednje:
x ⋅ y = 1
Kje očistiti in imeti:
y = 1/x.
Zgoraj navedeno je razlagano tako glede na vrednost x, prejšnja formula nam daje multiplikativno inverzno.
Možno je narediti svojo grafično predstavitev, kot je prikazano na naslednji sliki:
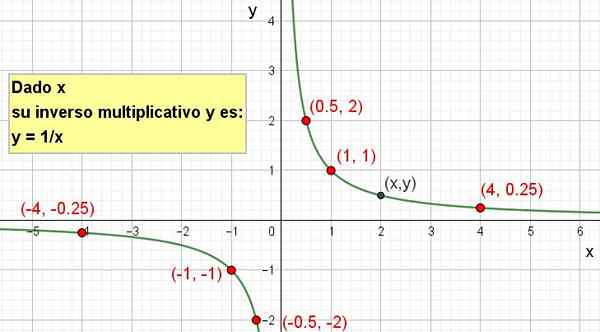 Slika 2. Multiplikativni obratni X je y = 1/x.
Slika 2. Multiplikativni obratni X je y = 1/x. Vaje
Vaja 1
Glede na x = 2 - √2, pridobite multiplikativno inverzno in.
Rešitev:
Tako, da in je multiplikativni x x
x ⋅ y = 1
X se nadomesti z njegovo vrednostjo:
(2 - √2) ⋅ y = 1
Potem se razčisti in:
y = 1 / (2 - √2)
Za racionalizacijo rezultata pomnoži števce in imenovalca s svojim konjugiranim binom:
y = (2 + √2) / ((2 + √2) (2 - √2))
V imenovalcu je prepoznaven izdelek, imenovan produkt vsote za razliko, kar je razlika na kvadratih. Na ta način koren izgine v imenovalcu.
y = (2 + √2) / (2^2 - (√2)^2)
Vam lahko služi: deležReševanje moči:
y = (2 + √2) / (4 - 2)
Poenostavitev:
y = (2 + √2) / 2
Vaja 2
Pridobite multiplikativno inverzno (1/A + 1/B), kjer sta A in B različna realna številka.
Rešitev:
Pokličemo in multiplikativno obratno (1/a + 1/b), tako da je treba izpolniti naslednjo enačbo:
In ⋅ (1/a + 1/b) = 1
Spremenljivka je očiščena in:
Y = 1/(1/a + 1/b)
Imenovalec je rešen:
Y = 1 / ((b + a) / a b)
Kot je znano o pravilih algebre, imenovalec imenovalca prenese na števca:
Y = (a b) / (b + a)
Naročeno je, da končno dobite:
(a b)/(a + b), ki je multiplikativni inverzni od (1/a + 1/b).
Vaja 3
Pridobite multiplikativno inverzno (a - b) / (a^2 - b^2).
Rešitev:
Spomnimo se, da se multiplikativni inverzni imenuje tudi vzajemna, ker se pridobi samo izmenjava števca in imenovalca.
Potem bo multiplikativna inverzna (a - b) / (a^2 - b^2):
(A^2 - b^2) / (a - b)
Toda ta izraz je mogoče poenostaviti, če po pravilih algebre prepoznamo, da je števca razlika kvadratov, ki jih je mogoče upoštevati kot produkt vsote za razliko:
(A + B) (A - B)) (A - B)
Ker je v števcu in imenovalcu skupni dejavnik (a - b), nadaljujemo s poenostavitvijo in končno pridobimo:
(A + B), kar je multiplikativno inverzno (A - B) / (A^2 - B^2).
Reference
- Viri, a. (2016). Osnovna matematika. Uvod v izračun. Lulu.com.
- Garo, m. (2014). Matematika: kvadratne enačbe: Kako reševanje kvadratne enačbe. Marilù Garo.
- Haeussler, npr. F., & Paul, r. S. (2003). Matematika za upravo in ekonomijo. Pearson Education.
- Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Matematika 1 sep. Prag.
- Dragoceno, c. T. (2005). Tečaj matematike 3o. Uredništvo Progreso.
- Rock, n. M. (2006). Algebra I je enostavna! Tako enostavno. Team Rock Press.
- Sullivan, J. (2006). Algebra in trigonometrija. Pearson Education.

