Matematika

Linearna interpolacija

Pojasnjujemo, kakšna je linearna medsebojna povezava, njene formule, kako narediti eno, s primeri in vajami, rešenimi

Kaj je linearna interpolacija?

The Linearna interpolacija Sestavljen je iz ocene lokacije točke v številčnem intervalu, ob predpostavki, da so skrajne vrednosti omenjenega intervala združene s črto. Znano enačbo te vrstice je mogoče najti neznano točko.

Ideja je shematizirana na naslednji sliki, ki prikazuje pristop k grafu funkcije med točkami A in B. Ob predpostavki, da so te točke blizu, je mogoče približati krivuljo, ki jih združuje skozi črto, in tako najti vmesne točke.

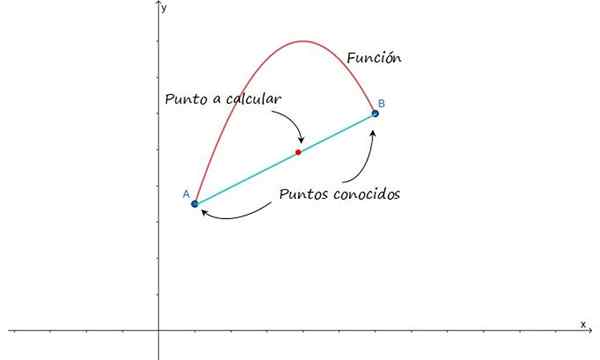Slika 1.- Za linearno interpolacijo med točkami A in B je treba domnevati, da jih združuje črta . Vir: f. Zapata.

Prav tako lahko približate krivuljo, ki se pridruži točkam, ki so bile dane s kvadratno funkcijo ali drugim polinomom. Vendar ima črta prednost svoje matematične preprostosti, zato je enostavno ravnati, čeprav je najpreprostejša interpolacija vseh, možno je, da rezultat ni tako natančen kot tisti, ki ga dobimo z uporabo drugih funkcij.

Formule

Obstajata dve koordinatni točki [x_tudi, f (x_tudi) in [x₁, f (x₁)] med katerimi je točka [x, g (x)], katerih koordinate so zaželene.

Prvi korak je vključevanje pri združevanju znanih točk skozi linijski segment, na katerem najdejo koordinate točke A izračuna.

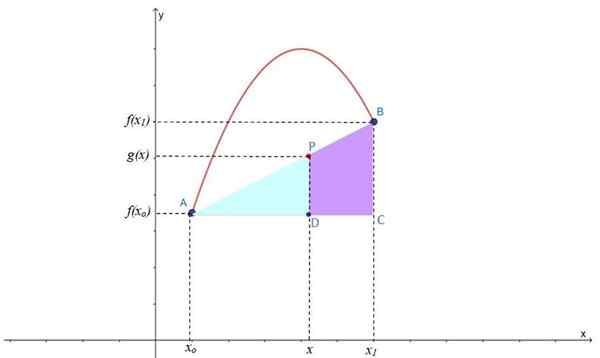Slika 2.- Linearna interpolacija za iskanje točke P na liniji prepletanja G (x), ki se nahaja med točkami A in B iz F (x). Vir: f. Zapata.

Kot lahko vidite, se oblikujejo dva pravokotnika: ABC in APD, ki imata tudi skupni akutni kot, tako da sta podobna trikotniki, za katere je mogoče uporabiti Thalesovo teorem:

Lahko vam služi: analitična geometrija

$\fracADAC=\fracAPAB=\fracPDBC$ Zamenjava mera segmentov v skladu z grafom dobimo naslednje razmerje:

$\fracx-x_ox_1-x_o=\fracg(x)-f(x_o)f(x_1)-f(x_o)$ Od tam nadaljujemo s čiščenjem g (x):

$g(x)=f(x_o)+\left [\fracf(x_1)-f(x_o)x_1-x_o \right ]\left ( x-x_o \right )$ Klicanje:

F₁(x₁) = y₁ ; F_tudi(x_tudi) = y_tudi; g (x) = y

Zgornja enačba se spremeni v:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Območje napak

Ko se s to metodo približuje funkcija, je stopnja napake podana z absolutno vrednostjo razlike med funkcijo f (x) in interpolacijsko črto G (x):

Napaka = │f (x) - g (x) │

Kako narediti linearno interpolacijo?

Izvajanje linearne interpolacije je zelo preprosto, samo slediti morate tem korakom:

Korak 1

Določite neznano točko P (x, y).

2. korak

Vzpostavite dve točki, ki omejujejo interval, kjer se nahaja vrednost, ki jo je treba izračunati, torej točke (x x_tudi,in_tudi) in (x₁, in₁).

Korak 3

Zamenjajte vse vrednosti v enačbi:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

In izračunajte rezultat.

Primeri linearne interpolacije

Primer 1

Z linearno interpolacijo želite najti približno vrednost Ln 3, glede na naslednje vrednosti:

ln 2 = 0.693147 in ln 4 = 1.386294

Primerjajte rezultat z vrednostjo ln 3, pridobljene s kalkulatorjem, in določite zavzeto maržo.

Korak 1

Če želite najti približno vrednost ln 3, morate nadaljevati po poti: Najprej je vzpostavljen neznano, ki je y = ln 3, poleg ustrezne vrednosti "x": x = 3. To je točka, ki jo želite izračunati: (3, ln 3).

2. korak

Potem morate z znanimi vrednostmi določiti mejne točke intervala. To se zahteva z naslednjimi točkami:

Spodnja meja: [x_tudi = 2; in_tudi = ln 2 = 0.693147]
Zgornja meja: [x₁ = 4; in₁ = ln 4 = 1.386294]
Korak 3

Vrednosti, določene v korakih 1 in 2, se v enačbi skrbno zamenjajo, da se ustvari rezultat pristopa k Ln 3:

Vam lahko služi: koliko rešitev ima kvadratna enačba?

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln\: 2+\left [\fracln4-ln24-2 \right ]\left (3-2 \right )$
$ln\: 3= 0.693147+\left [\frac1.386294-0.6931474-2 \right ]\left (3-2 \right )=1.039721$ Resnična vrednost ln 3, pridobljena s kalkulatorjem, je:

ln 3 = 1.098612

In stopnja napake je:

Napaka = │1.098612 - 1.03971 │ = 0.059

Odstotek napake interpolacije se izračuna tako, da napako delimo med resnično vrednostjo LN3 in pomnožimo za 100 %:

Odstotna napaka = (resnična napaka/vrednost) × 100 = (0.059/1.098612) × 100% = 5.4%

Primer 2

Zdaj želite najti približno vrednost ln 3 z linearno interpolacijo, poznana ta dve vrednosti:

ln 2.5 = 0.916291 in ln 3.5 = 1.252763

Določite tudi ustrezno napako in primerjajte z rezultati prejšnjega primera.

Korak 1

Spet je neznana točka:

y = ln 3, x = 3

2. korak
Spodnja meja: [x_tudi = 2.5; in_tudi = y_tudi = ln 2.5 = 0.916291]
Zgornja meja: [x₁ = 3.5; in₁ = ln 3.5 = 1.252763]
Korak 3

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln \: 2.5+\left [\fracln\: 3.5-ln \: 2.53.5-2.5 \right ]\left (3-2.5 \right )=1.084527$ Preučitev vrednosti, ki jo ponuja kalkulator:

ln 3 = 1.098612

V tem primeru je stopnja napake določena, kar ima za posledico:

Napaka = │1.098612 - 1.084527 │ = 0.014

Odstotek napake v tem primeru je ≈ 1.3 %. V primerjavi s stopnjo napake v primeru 1 je nova vrednost natančnejša, saj je interval, izbran za interpolar, nižji.

Rešene vaje

Vaja 1

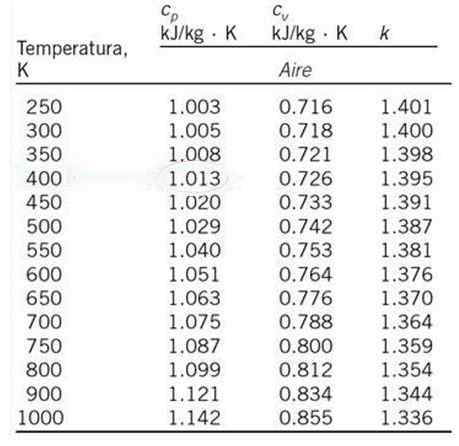
Z linearno interpolacijo izračunajte specifično toploto zraka pri konstantnem tlaku C_str in temperatura 530 K, začenši iz tabele vrednosti, prikazane spodaj.

Rešitev

Pri reševanju številnih težav je običajno, da se zahtevano vrednosti ne zdi natančno po želji v tabeli vrednosti. Druga možnost je, da izberete vrednost, ki je najbližje želenemu, vendar je večkrat linearna interpolacija dovolj, da najdete veliko boljši pristop.

Vam lahko služi: znaki združevanja

Vrednost c_str 530 K se ne prikaže v priloženi tabeli, vendar lahko linearno interpolacijo naredimo z ustreznimi specifičnimi vročina.

Ustrezne posebne toplote za te temperature so:

T_tudi = 500 K; c_po = 1.029 kJ /kg ∙ k

T₁ = 550 K; c_P1 = 1.040 kJ /kg ∙ k

In neznana je točka (500k, c_str)

Zamenjava v formuli linearne interpolacije, ki je bila navedena zgoraj, s t na prizorišču spremenljivke "x" in c_str Namesto "y" imate:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$c_p= c_po+\left [\fracc_p1-c_poT_1-T_o \right ]\left (T-T_o \right )$

$c_p= 1.029+\left [\frac1.040-1.029550-500 \right ]\left (530-500 \right )\frackJkg\cdot K=1.03536\frackJkg\cdot K$

Vaja 2

Obremenitev, ki se nanaša na vzmet (v kilopondiji), povzroči naslednje raztezanje (v milimetrih) v skladu s prikazano tabelo:

Izračunajte podaljšanje, ko je obremenitev 12.6 kp.

Rešitev

Naj in vrednost raztezka, ki je bila iskana, ko je obremenitev c = 12.6 kp. Neznana točka je (12.6, y), ki je med točkami:

C_tudi = 10 kp; in_tudi = 105 mm

C₁ = 15 kp; in₁ = 172 mm

Še vedno je nadomestiti vrednosti v enačbi:

$C= 105+\left [\frac172-10515-10 \right ]\left (12.6-10 \right )\: mm=139.84\: mm$ Predlagana vaja

Izračunajte specifično toplotno toploto na konstantno prostornino za temperaturo 727 K z uporabo linearne interpolacije in tabele vrednostnih papirjev vaje Rešene 1.

Reference

Akademija Rafa Vilchez. Kako izvesti linearno interpolacijo. Okrevano od: academiraafavilchez.com
CAPRA, s. 2007. Numerične metode za inženirje. 5. Izdaja. McGraw Hill.
Akademija Khan. Matematika linearne interpolacije. Okreval od: Khanacademy.org.
Izobraževalno življenje. Formula linearne interpolacije. Okrevano od: theeducationLife.com
X-Engineer. Linearna interpolacija in ekstrapolacija s kalkulatorjem. Okrevano od: X-Engineer.org.

Linearna interpolacija

Kaj je linearna interpolacija?

Formule

Območje napak