Interpolacija LaGrange

Kaj je Lagrangeova interpolacija?

Interpolacija Lagrangea je numerična metoda približevanja funkcij, ki uporablja polinom, ki prehaja skozi določene znane točke funkcije, ki naj bi se približala.

Če je približna funkcija mehka, tudi zunaj danih ali znanih vrednosti, polinom vzame vrednosti blizu vrednosti, ki vas zanima, še posebej, če so te vrednosti med danimi točkami. Zato polinom velja za dober pristop k funkciji.

Slika 1.- Formula za izgradnjo polinomov LaGrange. Vir: f. Zapata.

Zdaj, predpostavimo, da želite približno približati funkcijo f (x) od katerih so v nekaterih znani le njihove vrednote x-_Yo-, z Yo od 0 do N-1. Se pravi, da se poznata n točke (x-_Yo, in_Yo) z in_Yo = F (x_Yo), Kjer je indeks Yo Gre od 0 do N-1.

Pri metodi interpolacije LaGrange se polinom, ki se približa funkciji f (x) Je polinom P (x) stopnje N-1, zgrajena z linearno kombinacijo n Polinomi L_Yo(x) stopnje N-1. To so Polinomi LaGrange, ki so izražene na naslednji način:

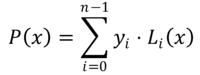
Vrednosti in_Yo Predstavljajo ordinate, ki ustrezajo abscisi x_Yo Kjer je funkcija f (x) Znano je, to je: in_Yo = F (x_Yo).

Polinomi LaGrange

Skozi linearne kombinacije med njimi delujejo polinomi LaGrange kot osnova za polinom gradbeništva N -1 ki bodo služili za interpolacijo n znane točke.

Zapis za polinome je l_Yo(x), z indeksom I v razponu od 0 do N-1. Formula za vzpostavitev polinomov LaGrange je naslednja:

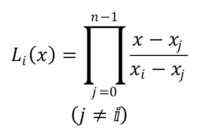
Prikazani simbol kaže, da je treba izvesti produkcijo N -1 monomov, začenši iz polinoma j = 0.

Značilnosti lagrange polinomov

1.- Lagrange polinomi so popolnoma enaki enoti, če jih ocenjujemo v abscisi, ki ustreza njihovemu indeksu, to je:

L_Yo(x_Yo) = 1

2.- Odpovedani so v abscisi interpolacijskih točk z indeksom, ki se razlikuje od istega polinoma:

Vam lahko služi: opisna statistika: zgodovina, značilnosti, primeri, koncepti

L_Yo(x_J) = 0, z i ≠ j.

3.- Če jemljemo druge vrednosti abscisa, ki se razlikujejo od interpolacijskih točk, polinomi Lagrange pridobijo vrednosti med -1 in +1.

4.- Za pridobitev polinomov Lagrange je treba le vedeti abscisa točk, da se Interpoch.

Drugi -stopinjski polinomi Lagrange

Drugi -stopinjski polinomi Lagrange so tisti, ki se najpogosteje uporabljajo, kadar želite opraviti interpolacijo s tremi točkami.

Recimo, da je interpolarna funkcija znana v treh točkah, ki so:

(x₀,in₀); (x₁, in₁); (x₂, in₂)

Nato vaši ustrezni polinomi LaGrange L₀, L₁ in L₂ Postanejo takole:

L₀(x) = [(x - x₁) / (X₀ - x₁) [(x - x₂) / (X₀ - x₂)

L₁(x) = [(x - x₀) / (X₁ - x₀) [(x - x₂) / (X₁ - x₂)

L₂(x) = [(x - x₀) / (X₂ - x₀) [(x - x₁) / (X₂ - x₁)

To je treba opozoriti L₀(x₀) = L₁(x₁) = L₂(x₂) = 1, medtem L_Yo(x_J) = 0 dokler Yo≠ j.

Interpolacijski polinom druge stopnje

Pomembno je opozoriti, da so v Lagrangeovem interpolacijskem polinomu redne interpolacijske točke Lagrange polinomni dejavniki.

Na ta način, ko polinomi dobijo za določene vrednosti abscisa, služijo za izračun interpolacijskega polinoma različnih funkcij.

V primeru interpolacije drugega razreda:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

In P (x) se v intervalu približa funkciji f (x) (x₀, x₂).

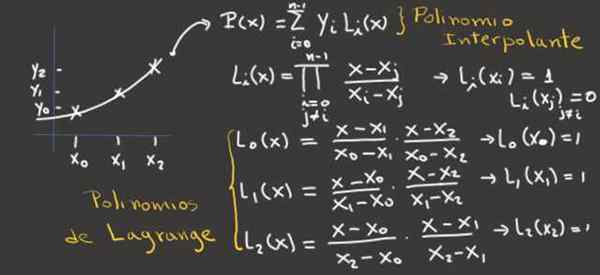Slika 2.- Ta slika prikazuje, kako pridobiti polinome Lagrange za tri interpolacijske točke in od njih, interpolirajoči polinom. Vir: f. Zapata.

Primeri

Primer 1

Poiščite lagrange polinome, ki ustrezajo trem točkam abscisa x₀= 0, x₁= 1 in x₂= 2.

Kot je razvidno v prejšnjem razdelku, bodo ti polinomi:

Lahko vam služi: Prevelika funkcija: definicija, lastnosti, primeri

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( x² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - x)

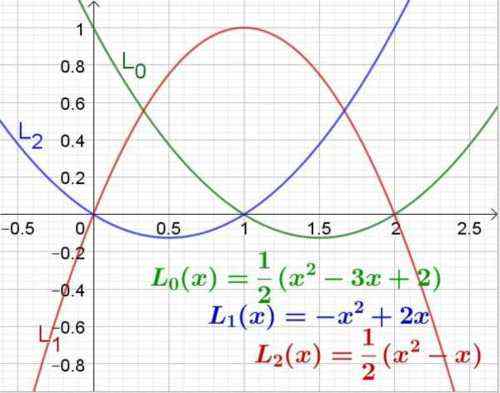Slika 3. Polinomi LaGrange za vrednosti abscisa 0, 1 in 2. Vir: f. Zapata.

Primer 2

Želite približno približati funkcijo f (x) = Arcan (x) V intervalu [0, 2]. Od te funkcije so znane samo njihove vrednote x₀= 0, x₁= 1 in x₂= 2, ki so in₀= 0, in₁= π/4 = 0,785 in in₂= 1,107.

Zato morate najti interpoling polinom P (x) približevanje f (x) V navedenem intervalu.

V primeru 1 so za vrednosti abscisa, navedene v tej izjavi, že določeni polinomi LaGrange, zato ni treba ponoviti izračuna. Interpoling polinom bo zdaj:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Ki je enakovredno:

P (x) = y₀ L₀(x) + in₁ L₁(x) + in₂ L₂(x)

V tem konkretnem primeru je:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0,785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - x)

Zgoraj je poenostavljeno:

P (x) = 0,785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - x)

In končno ostane:

P (x) = -0,2315 ∙ x² + 1.0165 ∙ x

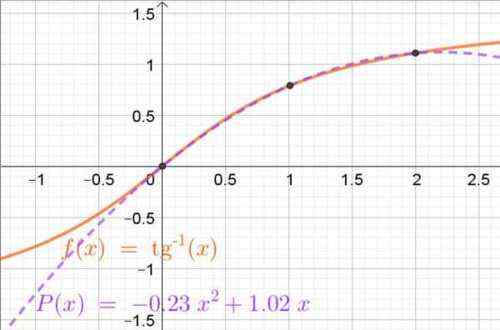Slika 4. Interpoling polinom, pridobljen s polinomi LaGrange, ki v intervalu približa funkcijo loka-tangenta (0, 2). Prikazane so tudi interpolacijske točke. Vir: f. Zapata.

Vaje

Vaja 1

Pridobite ustrezne lagrange polinome, da imajo pristop k funkciji:

f (x) = greh (x)

V intervalu [0, π] in s petimi interpolacijskimi točkami.

Rešitev

V prvi vrsti je določena abscisa interpolacijskih točk, ki so izbrani enaki in vključujejo konce približnega intervala. S tem imate:

x₀= 0; x₁= π/4; x₂= π/2; x₃= 3 π/4; x₄= π.

Vam lahko služi: neenakost trikotnika: demonstracija, primeri, rešene vaje

Ker je F (x) preklican na ekstremnih točkah, ne bo treba pridobiti lagrange l polinomov L₀ in l₄.

Polinomi l₁, L₂ in l₃ so:

L₁ = [(x - x₀) / (X₁ - x₀) [(x - x₂) / (X₁ - x₂) [(x - x₃) / (X₁ - x₃) [(x - x₄) / (X₁ - x₄)

L₂ = [(x - x₀) / (X₂ - x₀) [(x - x₁) / (X₂ - x₁) [(x - x₃) / (X₂ - x₃) [(x - x₄) / (X₂ - x₄)

L₃ = [(x - x₀) / (X₃ - x₀) [(x - x₁) / (X₃ - x₁) [(x - x₂) / (X₃ - x₂) [(x - x₄) / (X₃ - x₄)

Zdaj nadomestimo vrednost abscisa:

L₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

L₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

L₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Imenovalci so rešeni:

L₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - - - 3π/4)]

L₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

L₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - - - - π/4)]

Poenostavljeno in pregrupljeno je, da dobimo:

L₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

L₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

L₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Vaja 2

Pridobite interpolacijski polinom, ki se približa funkciji sen (x) v intervalu [0, π] s petimi interpolacijskimi točkami, izbranimi v vaji 1, in njihovimi polinomi LaGrange.

Rešitev

Interpolacijski polinom je:

P (x) = greh (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * l4

Ocenjevanje sinus in množenje funkcije je:

P (x) = (√2/2) l₁ + 1 * l₂ + (-Drug/2) l₃

Po napornem algebrskem delu je interpolacijski polinom:

P (x) = 2. 7481 x⁴ -petnajst. 138 x³ +23. 467 x² - 9. 5236 x

Reference

1. Goodman, a. L. H. Devetnajst devetdeset šest. Algebra in trigonometrija z analitično geometrijo. Pearson Education.
2. Harpe, str. d. (2000). Teme v teoriji geometrijske skupine. University of Chicago Press.
3. Hazewinkel, m. (2001). Linearna interpolacija ", enciklopedija matematike.
4. Hoffmann, npr. (2002). Do kronologije interpolacije: od starodavne astronomije do sodobne obdelave signalov in slik. Zbornik IEEE.
5. Wikipedija. Polinomska interpolacija LaGrange. Okreval od: Wikipedia.com