Trigonometrične identitete (primeri in vaje)

The Trigonometrične identitete To so razmerja med trigonometričnimi razlogi, ki veljajo za katero koli vrednost spremenljivke. Na primer:

Tan θ = sin θ /cos θ

Gre za trigonometrično identiteto, ki navaja tri razloge kot θ, tangent, dojko in kosinus omenjenega kota.

Slika 1. Nekatere trigonometrične identitete, ki se pogosto uporablja pri izračunu. Vir: f. Zapata.

Ta identiteta velja za vso vrednost, razen tistih, ki naredijo 0. Cos θ je 0 za θ = ± π/2, ± 3π/2, ± 5π/2… Drugi primer trigonometrične identitete je:

greh x . Sec x . CTG x = 1

[TOC]

Demonstracija

Obstajata dva osnovna načina, kako dokazati, da je trigonometrična identiteta resnična:

1- Preoblikovanje enega od članov enakosti v drugega z priročnimi algebrskimi manipulacijami.

2- Oba člana enakosti ločeno razvijeta, dokler ustrezni končni izrazi vsakega niso popolnoma enaki.

V predlagani identiteti bomo preoblikovali levo stran enakosti, za katero izražamo CTG X in Sec X glede na dojke in kosinusa na naslednji način:

Ctg x = cos x / sen x

Sec x = 1 /cos x

Ta izraz nadomestimo na levi strani identitete in poenostavimo:

greh x . (1/cos x). (cos x / sen x) = (greh x. cos x / cos x . sin x) = 1

In resničnost identitete je že dokazana.

Vrste trigonometričnih identitet

Obstaja več vrst trigonometričnih identitet. Nato bomo na kratko opisali glavne:

- Temeljne trigonometrične identitete

Razlikujemo dve vrsti temeljnih identitet:

I) Tisti, ki so izraženi iz osnovnih razlogov, kosinus in tangenta:

• Sec x = 1 /cos x
• Škoda x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) tisti, ki izhajajo iz paritete. Skozi njen graf vemo, da je sen x neparna funkcija, kar pomeni, da:

Vam lahko služi: 60 delitev

sin (-x) = - greh x

Zato je Cos X par, zato:

cos (-x) = cos x

Tako:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Podobno:

• cotg (-x) = -ctg x
• sec (-x) = sec x
• škoda (-x) = - škoda x

- Pitagorejske identitete

Oni so pridobljeni z uporabo teorema pitagore na pravokotnik trikotnika mačk A in B in Hypotenusa C. Pa poglejmo:

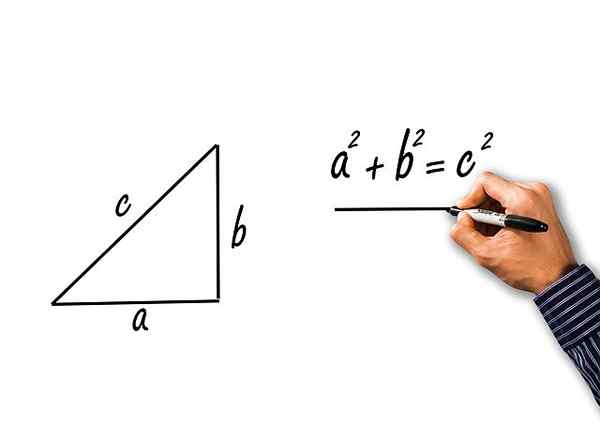Slika 2.- Iz teorema Pitagore dobimo tri pitagorejske trigonometrične identitete. Vir: Pixabay.

Teorem Pythagoras navaja, da:

c² = a² + b²

Delitev vsega med C²:

c² / c² = (a² / c²) + (B² / c²)

Izraz na levi je 1 in se spomnimo, da sta sinus in kosinus akutnega kota α opredeljena kot:

sin α = a/c

cos α = b/c

Rezultat:

1 = (sin α)² + (cos α)²

Ta identiteta je znana kot temeljna identiteta.

Postopek se lahko izvede z deljenjem med² in b², kar povzroči še dve identiteti:

Odst² α = 1 + tg² α

har² α = 1 + CTG² α

- Formule za kosinus in prsi vsote/odštevanja kotov

Glavne trigonometrične identitete za kosinus, dojke in tangent vsote in odštevanja so naslednje:

Predstavitev Sen (α + β) in CO (α + β)

Te identitete je mogoče prikazati geometrijsko ali tudi prek Eulerjeve formule:

in^iα = cos α + i sin α

Poglejmo, kaj se zgodi s formulo, ko zamenjamo vsoto dveh kotov α in β:

in^{I (α +β)} = cos (α + β) + i sin (α + β)

Ta izraz je zapleten, njen resnični del je cos (α + β), njen namišljeni del pa je i sin (α + β). Ta rezultat nadaljujemo, da ga uporabimo pozneje in se osredotočimo na razvoj eksponentnega dela:

in^{I (α +β)} = e^iα ⋅ e^iβ = (cos α + i sin α) . (cos β + i sin β) =

Vam lahko služi: šesterokotna prizma

= cos α⋅cos β + cos α⋅i sen β + i⋅sen α cos β - sen α⋅sen β

Pravi del tega izraza je tisti, ki ga namišljena enota "jaz" ne pomnoži:

cos α⋅cos β - sen α. Sen β

Namišljeni del je torej:

I (cos α⋅sen β + sen α⋅cos β)

Da bi bila dva zapletena izraza enaka, mora biti resnični del enega enak resničnemu delu drugega. Enako velja za namišljene dele.

Vzamemo shranjen rezultat in ga primerjamo s tem:

cos α. cos β - sen α. sin β = cos (α + β)

i (cos α⋅sen β + sen α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sen α⋅cos β)

- Formule za dvojni kot

V prejšnjih formulah vzamemo β = α in razvijemo:

sin (α + α) = sen 2 α = sen α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sen α⋅sen α = cos² α - sen ² α

TG (α + α) = Tg 2 α = [Tg α + Tg α] / [1- Tg α⋅tg α] = 2TG α / 1- TG² α

Če v drugem izrazu zamenjamo cos² α = 1 - Sen² α dobimo:

cos 2 α = cos² α- (1- cos² α) = 2 cos² α -1

- Formule na pol kota

V tem zadnjem izrazu nadomestimo α z α/2, naslednje ostane:

cos α = 2 cos ²(α/2) -1

Kraja:

Rešene vaje

- Vaja 1

Pokaži to:

Rešitev

Izraz bo algebraično delal, tako da bo videti desno. Kot v pravem izrazu se zdi sen x, je prvi korak izraziti COS²X v smislu sen x, tako da je vse v smislu istega trigonometričnega razloga:

Lahko vam služi: frakcija, enakovredna 3/5 (rešitev in razlaga)

Potem je 1 - Sen je dejavnik² x za razliko popolnih kvadratov. Če želite to narediti, se razjasni iz temeljne identitete:

cos²X = 1 - sen² x

1 - sen² x = (1- sin x) (1+senx)

In faktorizacija v prvotnem izrazu je nadomeščena:

Izraz (1-senx) je poenostavljen in enakost ostaja:

1 + sen x = 1 + senx

- Vaja 2

Rešite naslednjo trigonometrično enačbo in dajte rešitev za vrednosti med 0 in 360 °:

Tg x + sec² x = 3

Rešitev

V obdobju levice obstajata dva trigonometrična razloga, zato morate vse zmanjšati na enega, da boste lahko očistili neznano. Izraz sek² X se izraža skozi eno od pitagorejskih identitet:

Odst² α = 1 + tg² α

Z zamenjavo enačbe:

Tg x + 1 + tg² x = 3

Preurejanje izrazov:

Tg² x + tg x + 1 = 3

Ta enačba se reši s spreminjanjem spremenljivke:

tg x = u

ali² + U + 1 - 3 = 0 → u² + U - 2 = 0

To enačbo druge stopnje je enostavno rešiti s faktorizacijo:

(U +2) (u-1) = 0

Zato u₁ = -2 in u₂ = 1, enakovredno:

Tg x₁ = -2

Tg x₂ = 1

Končno:

x₁ = arctg (-2) = 296.6

x₂  = arctg (1) = 45 °

Reference

1. Carena, m. 2019. Priročnik za matematiko prednavdljivosti. Nacionalna univerza na obali.
2. Figuera, j. 1999. Matematika. 1. Raznovrstno. Bolivarske kolegijske izdaje.
3. Hoffman, J. Izbira vprašanj matematike. Zvezek 4.
4. Jiménez, r. 2008. Algebra. Dvorana Prentice.
5. Wikipedija. Trigonometrična identiteta in formule. Okrevano od: je.Wikipedija.org.
6. Zapata, f. 4 načini za reševanje enačbe druge stopnje. Okreval od: Francesfizike.Blogspot.com.
7. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.