Zgodovina geometrije ozadja in razvoja iz njenega izvora
- 4817
- 63
- Mr. Shane Larkin
The Zgodovina geometrije Začne se s prvimi civilizacijami, ki so to vejo matematike uporabile na praktičen način, zlasti narode Indo doline in Babilona, ki so poznali obtusene trikotnike, približno 3000 do.C.
V spisih egipčanskega pisca Ahmes (1550 do.C.) Metode se uporabljajo za izračun območja kroga. Babilonci so imeli splošna pravila za merjenje zvezkov in območij.
Ahme papirus ali matematični papirus RHIND Obe civilizaciji, Egipčani in Babilonci so poznali različice teorema Pitagore 1500 let pred pitagorejsko različico. Po drugi strani pa Indijci vedskega obdobja (od 1500-100 do.C.) rabljena geometrija v gradnji oltarjev.
[TOC]
Antična grčija
Grki so bili dolgo naklonjeni razvoju matematike. Liki, kot sta Pythagora in Platon, so povezani s številkami z vsem, kar obstaja na svetu. Zanje je bila matematika ključna za razlago vesolja; Ta ideal je sledil pri privržencih Pitagorejcev nekaj stoletij.
Zgodbe o Miletu
Tales de Mileto je bil eden prvih Grkov, ki je prispeval k napredku geometrije. Dolgo časa, preživet v Egiptu in iz teh naučenih osnovnih znanj. Bil je prvi, ki je vzpostavil formule za merjenje geometrije.
Zgodbe o Miletu Uspel mu je izmeriti višino egiptovskih piramid in meril njeno senco v natančnem trenutku, ko je bila njena višina enaka merilu njegove sence.
Pitagore
Pitagore V najpomembnejšem prispevku pitagore (569.C. - 475 a.C.) Do geometrije je znani teorem Pitagore, ki ugotovi, da je znotraj trikotnika pravokotnika kvadrat hipotenuze (stran, ki nasprotuje desnemu kotu) enak vsoti kvadratov preostalih stranic.
Elementi Euclida
Najpomembnejše delo, ki ga je rešilo že od antičnih časov, je bila študija Elementi, iz Euclid de alejandría (325 a.C. - 265 a.C.), narejeno v 300 -ih do.C. To je delo velike zgodovinske vrednosti, ki je kot osnova za poučevanje matematike že več kot 2000 let.
Euclid Elementi To je bila ena prvih knjig in sestavkov študij, ki je pojasnila matematična načela, ki jih je mogoče uporabiti za vsako situacijo. Vključuje postulate, ki so temeljna načela geometrije pri njihovem delu. Po drugi strani obstajajo kvantitativna načela, znana kot osnovni pojmi.
Euclid poučevanje Zmanjšanih gradbenih instrumentov znotraj geometrije na samo dva: pravilo brez ukrepov in kompasa. To je povzročilo tri klasične težave, ki niso našli odgovorov do devetnajstega stoletja: kvadrata kroga, podvajanje kocke in trisekcija kota.
Vam lahko služi: v tem stoletju so Španci osvojili Tenochtitlán?Za starodavne sta bili dve idealni geometrijski entiteti ravna črta in krog, zato je bila večina geometrijskih teoremov, ki so bili predlagani, produkt raziskovanja s temi instrumenti.
Geometrija v astronomiji
Geometrija je koristila tudi Grkom v smislu preučevanja zvezd. Izračunali so premike skozi opazovanje in izdelali geometrijske ravnine neba, ki so postavljale Zemljo kot osrednjo točko, ter sonce in luna ter drugi planeti in entitete, ki so se premikali okoli njih, in se vrteli v naboru krogov.
Eden najvplivnejših prispevkov je bil Almagest, Napisano v drugem stoletju D.C avtor Claudio Ptolemej (100 D. C.- 170 d.C), Astronomska pogodbena vsebnik kataloga zvezd. To je bilo najbolj popolno besedilo njegovega časa in je na transcendentalno vplivalo na astronomske študije, dokler ni srednji vek zelo napreden. To je bil del medijev, ki je najbolj populariziral geocentrični sistem, ki je trdil, da je zemlja središče vesolja.
Ptolomej Islamski vpliv
Proti IX stoletja, ko je bil arabski svet v veliki širitvi, je večina svoje kulture prežela več področij znanosti in umetnosti. Bili so veliki oboževalci matematičnih in filozofskih del Grkov.
Ena najbolj raziskanih vej v njihovih potrebah je bila astronomija, da bi poiskali natančno orientacijo, v kateri naj bi MECA izvajal stavke.
Po študijah euklida in drugih prispevkov, kot so Ptolomeji, so muslimani razvili stereografsko projekcijo, to je projekcija nebesne sfere v ravnini, da bi jo uporabila kot zemljevid. To je pomenilo napredek pri preučevanju trigonometrije.
Med najbolj reprezentativnimi liki je Thābit Ibn Qurra (826/36-901), ki je naredil ustrezne prevode starodavnih besedil Apolloniusa, Archimeda, Euclida in Ptolomeja. Nekatere od teh so edine preživele različice starodavnih spisov.
Raziskave v zvezi z astronomsko geometrijo so omogočile tudi ustvarjanje enega najbolj reprezentativnih instrumentov, Astrolabio, ki je poenostavil astronomske izračune trenutka. Poleg tega jim je ta instrument omogočil tudi, da poznajo čas in končno dobijo smernice za MECA.
Lahko vam služi: 8 carine in tradicije MixtecsEvropski razvoj zapuščine
V dvanajstem stoletju, po vstavitvi klasičnih naukov Grkov, zahvaljujoč muslimanski širitvi in razvoju njihovih istih odkritij, so se prevodi latinskih besedil začeli izvajati neposredno iz grščine ali iz arabskega jezika.
To bi pomenilo novo učenje v Evropi, ki bi ga promovirala renesansa. Ponovno odkritje pojmov, kot so "dokazi", se je začel koncept med Grki, ki jih je v resnici zanimalo prikaz postulatov.
Geometrija v umetnosti
Znanje se je odražalo tudi v umetnosti, kot sta slikarstvo ali arhitektura, saj bi geometrija začela biti temeljni del razvoja perspektive v umetnosti.
Filippo Brunelleschi (1377-1446) je bil tisti, ki je z matematiko uspelo razviti linearno perspektivo. Cilj te teorije je bil v letalu predstavljati tridimenzionalni prostor od tega, kako ga je dojemalo človeško oko. Tako ugotovi, da so se morale vse črte na sliki zbližati ali najti puščanje, da bi ustvarile občutek globine.
Filippo Brunelleschi. Vir: i, sailko/cc by-s (http: // creativeCommons.Org/licence/by-sa/3.0/) Brunelleschi je prvi opisal perspektivo kot znanstveni postopek in to je delovalo kot osnova za kasnejša delovna mesta znotraj umetnosti.
V drugih primerih uporabe geometrije pri preučevanju umetnosti in človeškega bitja je delo Leonarda da Vincija (1452 -1519) v njegovi risbi Moški Vitruvio. Gre za študijo, ki temelji na najbolj popolnih razmerjih za človeško telo z geometrijsko analizo njegove strukture.
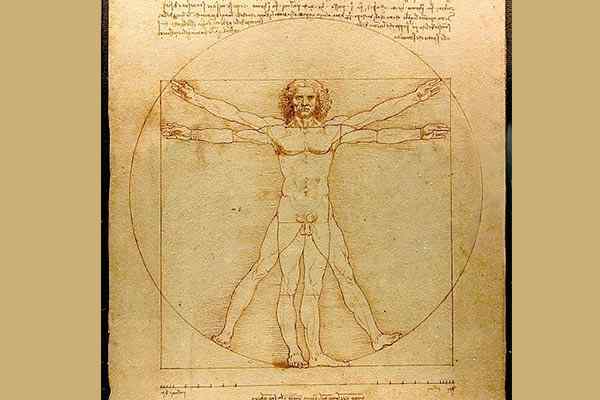Človek razstave Leonarda da Vinci / Public Domain Med drugim izstopa tudi arhitektura, kjer so se začeli pojavljati različni elementi, kot sta simetrija in ravnovesje. Kvadratna, pravokotna vrata in okna, nameščena na uravnotežen način; Uporaba klasičnih elementov antike, kot so stolpci, kupoli in trezorji.
Korak do sodobnosti
Analiza perspektiv in projekcij med renesanso je bila ena od spodbud za vzbujanje interesa matematikov. Od tega trenutka naprej se v geometriji začnejo ustanavljati bolj trdne in zapletene matematične baze.
Eno najpomembnejših del za modernost je bilo, da je arhitekt Girard Rasard (1591-1661), ki naj bi začetek projektivne geometrije. Po eni strani je ugotovilo, da se morajo vzporedne črte v projekciji zbližati v točki na neskončni črti, to je obzorje.
Vam lahko služi: Tuxtepec Rebellion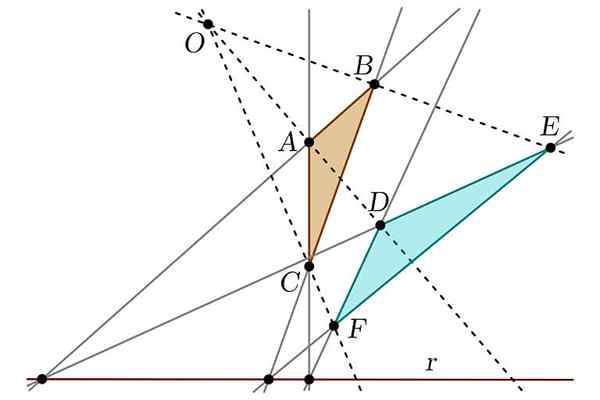
Teorem o neredu Po drugi strani je odkril tudi, kaj bi bilo prepoznano kot teorem o nereševalniku, ki vzpostavlja odnos med dvema številkama, ki se lahko štejeta za "projektivno". Odgovoren je bil tudi za poenostavitev Apolloniusovih del glede na odseke stožca, s čimer so analogije med to številko in valjem naredili analogije.
Drug velik dogodek tega obdobja je bilo ustvarjanje analitične geometrije s študijami Renéja Descartesa (1596-1650) in Pierre de Fermat (1601-1665). To je študija geometrije z uporabo koordinatnega sistema.
René Descartes, ki dela na namizju. Wikimedia Commons Neevklidska geometrija
Proti 18. in 19. stoletju so se začele študije v neevklidski geometriji. Konkretno so bili Gauss, Johann Boleai in Lobachevsky, ki so ugotovili, da petega postulata Euclida, znanega kot vzporedni postulat, ni mogoče preveriti.
Na ta način so razvili vrsto geometrije, v kateri je bil ta postulat kvalificiran kot napačen. Ta nova oblika je bila uspešna, saj je dajala zadovoljive rezultate v stilih geometrije, ki niso nujno ustrezali vsem evklidnim postulatom. Tako sta se pozneje rodila hiperbolična geometrija in eliptična geometrija.
V 18. stoletju je vredno poudariti delo Leonharda Eulerja (1707-1783) glede na razvoj matematične zapisovanja. Nato bi dvajseto stoletje s seboj prineslo razvoj bolj specifičnih polj geometrije, med katerimi so:
-Algebrska geometrija: To je veja matematike, ki združuje abstraktno algebro in analitično geometrijo.
-Končna geometrija: Gre za geometrijski sistem, ki je sestavljen iz končne količine točk, to je, da imajo konec ali omejitev, zato jih je mogoče izmeriti.
-Digitalna geometrija: To je veja računalništva, da je preučevanje algoritmov in podatkovnih struktur, ki jih je mogoče predstaviti v geometrijskih izrazih.
Reference
- (2016), kar je postalo Euclid Elements edina knjiga, ki lahko tekmuje s Biblijo. BBC. BBC je bil obnovljen.com
- Trije klasični problemi grške matematike. Univerza v Antiokiji. Okreval od poučevanja.ti.Edu.co
- Heilbron J.L (2020). Geometrija. Encyclopædia Britannica. Okreval od Britannice.com
- Zgodovina geometrije. Wikipedia, brezplačna enciklopedija. Pridobljeno iz.Wikipedija.org
- Analitična geometrija. Wikipedia, brezplačna enciklopedija. Pridobljeno iz.Wikipedija.org
- (2017) Geometrija in matematika v renesansi. Okreval od ukessays.com
- Sáiz a. Linearna perspektiva v Brunelleschiju. Univerza v Valenciji. UV je bil obnovljen.je
- Uredniki Encyclopeedia Britannica (2019). Renesančna arhitektura. Encyclopædia Britannica. Okreval od Britannice.com
- Andersen K (2020). Girard je razorožen. Encyclopædia Britannica. Okreval od Britannice.com
- (2011) zanimiv uvod v računsko geometrijo. Pridobljeno od Gaussov.com