Homotecia

The Homotecia Gre za geometrijsko spremembo v ravnini, kjer se od fiksne točke, imenovane center (o), razdalje pomnoži s skupnim faktorjem. Na ta način vsaka točka P ustreza drugi točki transformacije in te so poravnane s točko ali.

Potem je homotecia dopisovanje med dvema geometrijskima figurama, kjer se transformirane točke imenujejo homotetične, in te so poravnane s fiksno točko in z vzporednimi segmenti drug z drugim.

Pojasnilo in formula

Homotecia je preobrazba, ki nima skladne slike, saj bodo s številke pridobili eno ali več številk večje ali manjše velikosti kot prvotna številka; to pomeni, da homotecia pretvori poligon v drugega podobnega.

Da bi se Homotecia izpolnila, mora ustrezati točke do točke in ravno črto, tako da so pari homolognih pik poravnani s tretjo fiksno točko, ki je središče homotecije.

Prav tako morajo biti pari linij, ki jih združujejo. Razmerje med takimi segmenti je konstanten imenovan razlog homotecia (k); Na tak način, da je homotecija mogoče opredeliti kot:

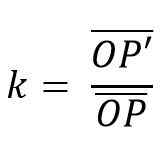
Za to vrsto preobrazbe se začne poljubna točka, ki bo središče homotecije.

Od tega trenutka se za vsako točko figure narišejo segmenti linij, ki jo je treba preoblikovati. Lestvica, na kateri je narejena reprodukcija nove številke, je podana iz razloga za homotecijo (k).

Lastnosti homotecia

Ena glavnih lastnosti homotecije je, da so zaradi razloga za homotecijo (k) vse homotetične figure podobne. Med drugimi izjemnimi lastnostmi so naslednje:

Lahko vam služi: sestavljena sorazmernost: razlaga, tri sestavljene pravila, vaje

- Center Homotecia (O) je edina dvojna točka in se preoblikuje; Se pravi, da se ne razlikuje.

- Črte, ki gredo skozi središče, postanejo sami (so dvojne), vendar točke, ki ga sestavljajo, niso dvojne.

- Črte, ki ne gredo skozi sredino, se spremenijo v vzporedne črte; Na ta način ostajajo koti homotecije enaki.

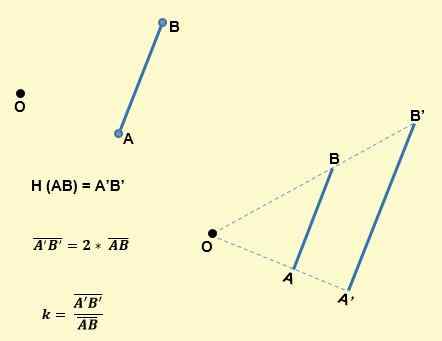
- Podoba segmenta s središče homotecije ali razloga K je od segmenta vzporedna in ima k kratke dolžine. Na primer, kot je razvidno iz naslednje slike, bo AB segment za Homotecia še en segment A'B ", tako da bo AB vzporeden z A'B" in K bo:

- Homotetični koti so skladni; to pomeni, da imajo isti ukrep. Zato je slika kota kot, ki ima enako amplitudo.

Po drugi strani je treba homotecia spreminjati glede na vrednost njegovega razuma (k) in lahko pride do naslednjih primerov:

- Če konstanta k = 1, so vse točke fiksirane, ker se preoblikujejo. Tako homotetična figura sovpada z izvirnikom in transformacija se imenuje identitetna funkcija.

- Če je K ≠ 1, bo edina fiksna točka središče homotecije (o).

- Če je k = -1, homotecia postane osrednja simetrija (c); To pomeni, da se bo vrtela okoli C, pod kotom 180^tudi.

- Če je K> 1, bo velikost preoblikovane figure večja glede na velikost izvirnika.

Vam lahko služi: iracionalne številke: zgodovina, lastnosti, klasifikacija, primeri

- DA 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.

- Da -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.

- Ja k < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.

Vrste homotecije

Homotecia bi lahko razvrstili tudi v dve vrsti, odvisno od vrednosti njegovega razuma (K):

Neposredna homotecia

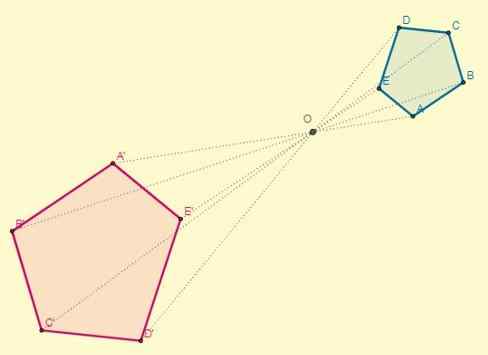
Se pojavi, če konstantna k> 0; To pomeni, da so homotetične točke na isti strani glede na središče:

Faktor sorazmernosti ali razmerje podobnosti med neposrednimi homotetičnimi številkami bo vedno pozitivno.

Inverzna homotecija

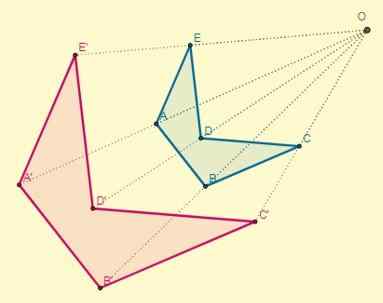
Se pojavi, če konstanta k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:

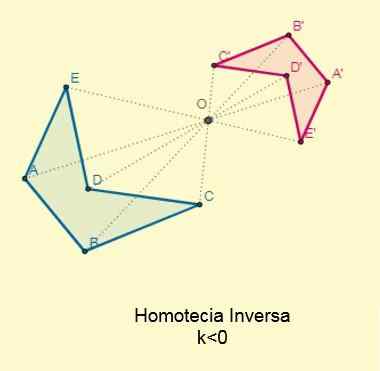
Faktor sorazmernosti ali razmerje podobnosti med obratnimi homotetičnimi številkami bo vedno negativno.

Kompozicija

Ko se zaporedoma izvaja več gibov, dokler se številka, enaka izvirniku, pojavi sestava gibov. Sestava več gibov je tudi gibanje.

Sestava med dvema homotecijo povzroči novo homotecijo; To pomeni, da obstaja izdelek homotecia, v katerem bo središče poravnano s sredino obeh prvotnih preobrazb, razlog (k) pa je produkt obeh razlogov.

Tako v sestavi dveh homotij h₁(Bodisi₁, k₁) in h₂(Bodisi₂, k₂), Množenje vaših razlogov: k₁ x k₂ = 1 bo povzročila homotecijo razloga K₃ = K₁ x k₂. Središče te nove homotecije (ali₃) se bo nahajal na črti oz₁ Tudi₂.

Lahko vam služi: nasproti kotov z točko (z rešeno vajo)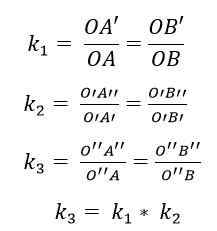

Homotecia ustreza ravni in nepovratni spremembi; Če se uporabljata dve homotecia, ki imata isto središče in razum, vendar z drugačnim znakom, bo prvotna številka pridobila.

Primeri homotecije

1. Prvi primer

Nanesite homotecijo na dani poligon centra (o), ki se nahaja 5 cm od točke A in katerih razlog je K = 0,7.

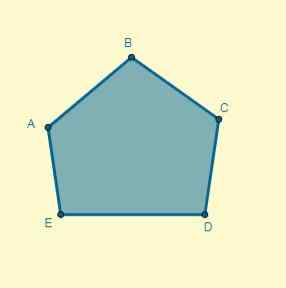
Rešitev

Vsaka točka je izbrana za središče homotecije, od tega pa jih trgujejo z vrhovi figure:

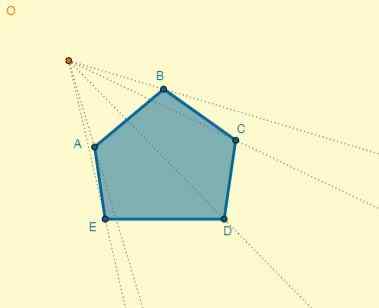
Razdalja od središča (o) do točke A je oa = 5; S tem lahko določite razdaljo ene od homotetičnih točk (oa '), ki ve, da je k = 0,7:

Oa '= k x oa.

Oa '= 0,7 x 5 = 3,5.

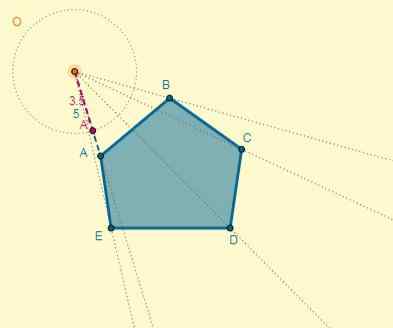
Postopek je mogoče izvesti za vsako točko, ali pa lahko narišete tudi homotetični poligon in se spomnite, da imata dva poligona vzporedne strani:

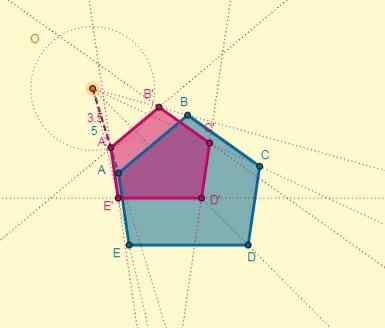
Končno je preobrazba videti na naslednji način:

2. Drugi primer

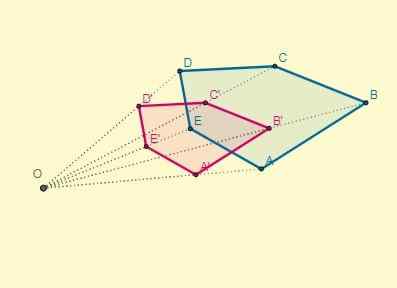
Nanesite homotecijo na dani poligon centra (o), ki se nahaja 8,5 cm od točke C in katerih in razlog K = -2.

Rešitev

Razdalja od središča (O) do točke C je OC = 8,5; S temi podatki je mogoče določiti razdaljo ene od homotetičnih točk (OC '), prav tako vedoč, da je k = -2:

Oc '= k x oc.

Oc '= -2 x 8,5 = -17

Po risanju segmentov vrhov transformiranega poligona so začetne točke in njihova homotetika nameščena na nasprotnih koncih glede na center: