Izometrične transformacije

The Izometrične transformacije So spremembe položaja ali orientacije določene številke, ki ne spreminjajo oblike ali velikosti tega. Te transformacije so razvrščene v tri vrste: prevod, vrtenje in odsev (izometrija). Na splošno geometrijske transformacije omogočajo ustvarjanje nove številke iz drugega danega.

Preobrazba v geometrijsko figuro pomeni, da je bila na nek način podvržena nekaterim spremembam; to pomeni, da je bilo spremenjeno. Glede na občutek izvirnika in podobne v ravnini lahko geometrijske transformacije razvrstimo v tri vrste: izometrične, izomorfne in anamorfne.

Značilnosti izometričnih transformacij

- Izometrične transformacije se pojavijo, ko se ohranijo veličini segmentov in kotov med prvotno in preoblikovano figuro.

- Pri tej vrsti preobrazbe oblika ali velikost slike ni spremenjena (so skladni), le sprememba položaja tega, bodisi v orientaciji ali v smislu. Na ta način bosta začetna številka in končna podobna in geometrijsko skladna.

- Izometrija se nanaša na enakost; to pomeni, da bodo geometrijske figure izometrične, če imajo enako obliko in velikost.

- Pri izometričnih transformacijah je edino, kar lahko opazimo, sprememba položaja v ravnini, togo gibanje se pojavi zahvaljujoč prehajanju iz začetnega položaja v končni položaj. Ta številka se imenuje homologna (podobna) izvirnika.

- Obstajajo tri vrste gibov, ki razvrščajo izometrično transformacijo: prevod, vrtenje in odsev ali simetrija.

Vrste izometričnih transformacij

S prevodom

So tiste izometrije, ki omogočajo, da se v ravni črti presežejo vse točke ravnine v določeni smeri in razdalji.

Ko se številka pretvori s prevodom, ne spremeni svoje orientacije glede na začetni položaj, niti ne izgubi svojih notranjih ukrepov, ukrepov njegovih kotov in stranic. To vrsto premika je opredeljen s tremi parametri:

• Naslov, ki je lahko vodoraven, navpičen ali poševen.
• Smer, ki je lahko levo, desno, navzgor ali navzdol.
• Razdalja ali velikost, ki je dolžina, ki je od začetnega položaja do končnega od katere koli točke, ki se premakne.

Vam lahko služi: curtoza: definicija, vrste, formule, za kaj je na primer

Za izometrično transformacijo zaradi prevoda mora izpolnjevati naslednje pogoje:

• Slika mora vedno hraniti vse svoje dimenzije, tako linearne kot kotne.
• Slika ne spremeni svojega položaja glede na vodoravno os; Se pravi, njen kot se nikoli ne razlikuje.
• Prevodi bodo vedno povzeti v enem, ne glede na število narejenih prevodov.

V ravnini, kjer je središče točka ali, s koordinatami (0,0), je prevod opredeljen z vektorjem T (A, B), kar kaže na premik začetne točke. To pomeni:

P (x, y) + t (a, b) = p '(x + a, y + b)

Na primer, če se uporabi za koordinatno točko P (8, -2), se uporabi prevod T (-4, 7), dobimo:

P (8, -2) + t (-4, 7) = p '[(8 + (-4)), ((-2) + 7)] = p' (4, 5)

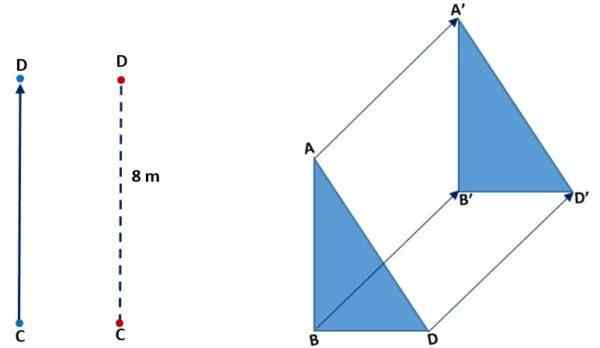
Na naslednji sliki (levo) lahko vidite, kako se je točka C premaknila na sovpadanje z D. To je storil navpično, pomen se je dvignil in razdalja ali magnituda je bila 8 metrov. Na pravi sliki opazimo prevod trikotnika:

Z vrtenjem

So tiste izometrije, ki omogočajo, da figura obrne vse točke ravnine. Vsaka točka se zavrti po loku, ki ima konstanten kot in določeno fiksno točko (zavoj).

To pomeni, da bo vse vrtenje določeno z vrtenjem in kotnim sredino. Ko se številka preoblikuje z vrtenjem, vzdržuje mero svojih kotov in stranic.

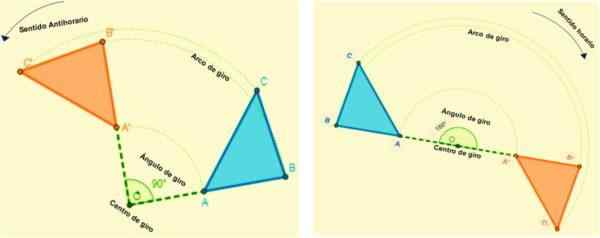
Vrtenje se pojavi v določeni smeri, pozitiven je, ko je zavoj protinorojen (v nasprotju s tem, kako se roke ure vrtijo) in negativno, ko je njegov na zavod v smeri urinega kazalca.

Če se točka (x, y) vrti glede na izvor -to je, da je njegov vrteči se (0,0) -pod kotom 90^tudi 360^tudi Koordinate točk bodo:

Vam lahko služi: statistične veje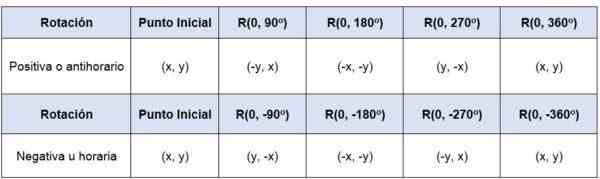

V primeru, v katerem rotacija nima središča pri izvoru, je treba izvor koordinatnega sistema na nov izvor prenesti, da se vrti figuro, ki ima izvor središče.

Na primer, če se uporabi točka p (-5,2) 90 vrtenja^tudi, Okoli izvora in v pozitivnem smislu bodo nove koordinate (-2,5).

Z odsevom ali simetrijo

So tiste transformacije, ki vlagajo točke in številke letala. Ta naložba je lahko v zvezi s točko ali pa je lahko tudi glede na linijo.

Z drugimi besedami, pri tej vrsti transformacije je vsaka točka na prvotni sliki povezana z drugo točko (slika) homologne figure, tako da sta točka in njegova slika na isti razdalji od črte, imenovane simetrična os.

Tako bo levi del slike odsev desne strani, ne da bi spremenil obliko ali njene dimenzije. Simetrija preoblikuje enako figuro, vendar v obratni strani, kot je razvidno iz naslednje slike:

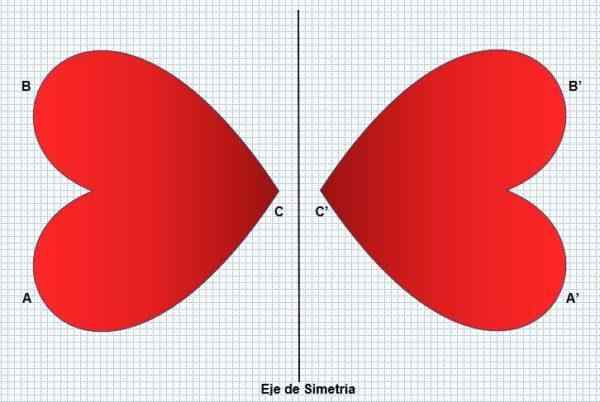
Simetrija je prisotna v mnogih vidikih, kot so nekatere rastline (sončnice), živali (pav) in naravni pojavi (snežinke). Človek ga odraža v njegovem obrazu, kar velja za lepotni dejavnik. Razmislek ali simetrija je lahko dveh vrst:

Centralna simetrija

To je tista transformacija, ki se zgodi glede na točko, v kateri lahko številka spremeni svojo orientacijo. Vsaka točka na prvotni sliki in njena slika je na isti razdalji od točke ali, imenovana Symmetry Center. Simetrija je osrednja, ko:

• Tako točka kot njegova podoba in središče pripadata isti vrstici.
• Z vrtenjem 180^tudi od središča ali številke, ki je enaka izvirniku.
• Stroki začetne številke so vzporedni z udarci oblikovane slike.
• Pomen figure se ne spreminja, vedno bo v urniku.

Vam lahko služi: koliko morate dodati 3/4, da dobite 6/7?

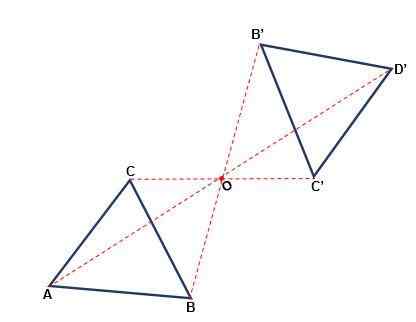Aksialna simetrija

Ta transformacija se zgodi glede na osi simetrije, kjer je vsaka točka na začetni sliki povezana z drugo točko na sliki in ta so na isti razdalji kot os simetrije. Simetrija je osna, ko:

• Segment, ki se pridruži točki s svojo sliko, je pravokoten na osi simetrije.
• Številke spreminjajo svoj pomen glede na smer zavoja ali časa.
• Z delitvijo figure z osrednjo črto (simetrična os) ena od nastalih polovic popolnoma sovpada z drugo od polovic.

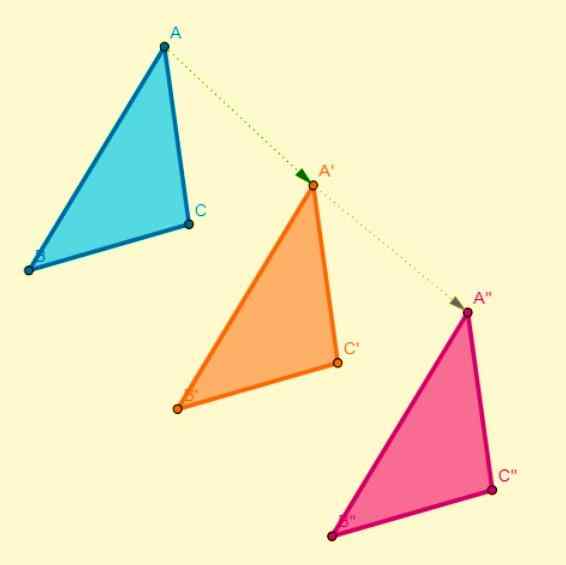
Kompozicija

Sestava izometričnih transformacij se nanaša na zaporedno uporabo izometričnih transformacij na isti sliki.

Sestava prevoda

Sestava dveh prevodov povzroči še en prevod. Ko se izvaja na ravnini, se na vodoravni osi (x) spreminjajo samo koordinate te osi, medtem ko koordinate navpične osi (y) ostanejo enake in obratno.

Sestava vrtenja

Sestava dveh zavojev z istim centrom povzroči drug zavoj, ki ima isto središče in katerih amplituda bo vsota amplitud obeh zavojev.

Če ima center zavoji drugačno središče, bo rez obeh segmentov podobnih točk središče vrtenja.

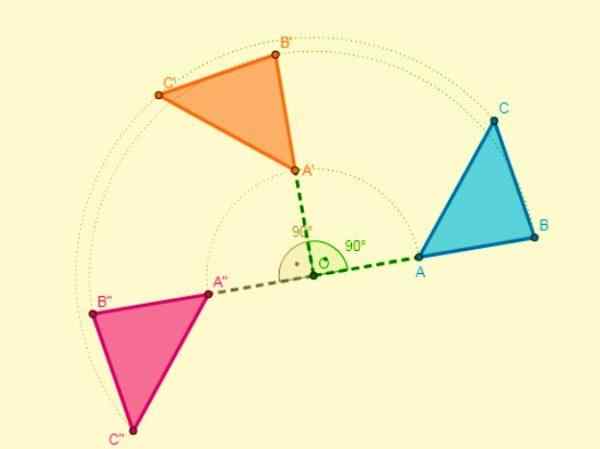
Sestava simetrije

V tem primeru bo sestava odvisna od tega, kako se uporablja:

• Če se dvakrat uporablja ista simetrija, bo rezultat identiteta.
• Če se za dve vzporedni osi uporabljata dve simetriji, bo rezultat prevod, njihov premik pa je dvakrat večja od teh osi:

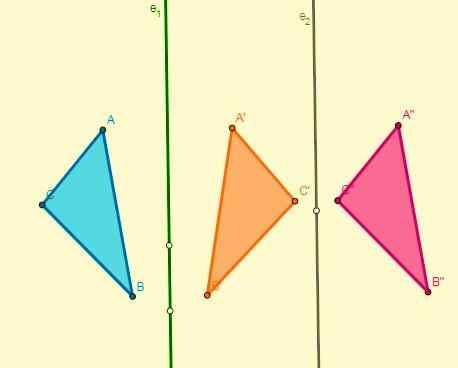
• Če se naneseta dve simetriji glede na dve osi, ki sta razrezani v točki O (sredinski), bo pridobljena vrtenje s sredino in njegov kot bo dvakrat večji kot, ki ga tvorijo osi: