Zgodovina trigonometrije iz njegovega izvora

The Zgodovina trigonometrije Nanaša se na nabor dejstev in napredka, ki se je zgodil okoli te veje matematike od njegovega izvora do najnovejših dogodkov.

Pri kratkem potovanju skozi svojo zgodovino je razvidno, da se je ta znanost rodila kot odgovor na težave, s katerimi se soočajo starodavni astronomi in navigatorji za analizo premika zvezd na nebu.

Izraz se prvič pojavlja v knjigi Trigonometriae Libri Quinque, ki sta jo napisala nemški matematik in znanstvenik Pitiscus Bartolomé (1561-1613). Prek Wikimedia Commons.

Prav tako beseda trigonometrija izhaja iz sestave dveh grških besed: Trigonon (Trikotnik) in Metron (obseg). Izraz se prvič pojavi v knjigi Trigonometriae libri quinque, Napisal nemški matematik in znanstvenik Pitiscus Bartolomé (1561-1613).

Na ta način etimologija besede kaže, da je trigonometrija študija odnosov med koti trikotnika in segmenti ali črtami, ki ga tvorijo.

[TOC]

Začetki trigonometrije

Prve korake trigonometrije je opravil človek, ko jih je spodbujala potreba po poznavanju in analiziranju gibanja zvezd.

To pomeni, da je človeško bitje zasnovalo trigonometrijo, ker so ga našli v situacijah, ko je bilo nemogoče neposredno izvesti meritev, saj je bilo za izračun zvezd potrebno bolj zapletena matematična orodja.

- Študije v Babilonu

Mladna miza, ki so jo napisali Babilonci, imenovani Plimpton 322. Via: Wikimedia Commons

Študije kažejo, da to pred več kot 3.000 let Babilonci so že obravnavali koncept kotnih in trigonometričnih razlogov.

Na primer mizo z blatom, ki so jo napisali Babilonci Plimpton 322 (1800 a. C.) prikazuje nasledstvo stolpcev in vrstic, ki vsebujejo številke v pisanju Cunoiform. Glede na raziskave, ki jih izvajajo nekateri strokovnjaki, ta tablični računalnik predstavlja tisto, kar se zdi niz trigonometričnih funkcij.

Vam lahko služi: kakšna je smernica? (Geometrija)

Babilonci so bili seznanjeni s koncepti, ki so povzročili pitagora 'izrek (569-474 a.C) in razumeli so svoje načelo.

Na enak način so poznali tudi teorem, ki ga pripisujejo Thalesu iz Miletusa (695-546 do.C), kar kaže, da vsak ravno, narisan vzporedno s stranjo trikotnika, z drugimi dvema stranema tvori še en trikotnik, ki je podoben začetnemu trikotniku.

- Stari Egipčani

Starim Egipčanom je uspelo enakomerno vzdrževati pobočje na vsakem od piramidnih obrazov. Via: Pixabay

Čeprav ni primerno govoriti o trigonometriji v splošni sferi egipčanske matematike, ni dvoma, da je ta civilizacija obravnavala določene trigonometrične koncepte.

To se zgodi, ker je mogoče pri razmišljanju o velikih zgradbah, ki so jih ustvarili Egipčani, na primer piramide, sklepati, da imajo nekaj znanja o trigonometriji.

Osnovna inženirska težava, s katero se soočajo Egipčani - in to se je rešilo neverjetno.

Za to so uporabili koncept, ki so ga imenovali "SEQT", in to je enakovredno tistemu, kar danes razumemo kot naklon nagnjene ravne površine.

Poleg tega Egipčani naredijo meritve na navpičnih površinah, ki se uporabljajo kot enota "komolec" in v vodoravni "roki", ki je ustrezala 1/7 komolca. Na ta način so izračunali seqt ali v različnih stavbah. Na primer, v piramidi Jufú (čakalna vrsta) je SEQT 5 1/2 roke na komolčni.

- Starodavna Grčija in godalna miza

Vse znanje Babiloncev in starih Egipčanov je šlo v Grčijo, kjer je bil poudarjen matematik in astronom Nicea (190-120 (190-120. C), ki velja za oče trigonometrije. Hiparco je ustvaril mize "strun", s katerimi mu je uspelo rešiti težave z ravnimi trikotniki.

Nicea Hiparco - Vir: Preneseno iz.WIKIPEDIA TO COMMONS BY MAKSIM - V DAVNI DOMAJI

Da bi jih naredili, je uporabil obseg z določenim polmerom (polmer je razdalja med sredino kroga in katero koli točko oboda).

Vam lahko služi: pogojna verjetnost: formula in enačbe, lastnosti, primeri

Nato je bil polmer, da je določil različne kote; Medtem ko je to v tabeli kazalo na dolžino črte, ki je bila omejena na straneh kota in oboda.

Te "strune" so se izkazale za predhodnice tabel trigonometričnih funkcij, ki jih uporabljamo danes.

- Indijski prispevki

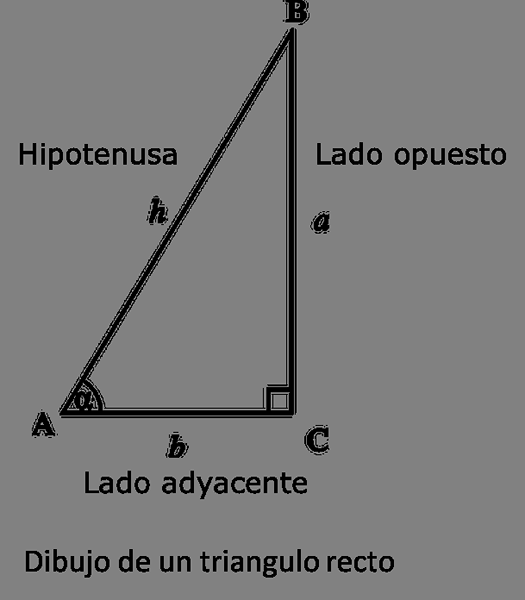Risba desnega trikotnika.

Tako kot grški znanstveniki so tudi Indijski astronomi razvili trigonometrični sistem, vendar so za razliko od Grkov, ki so ti astronomi temeljili na svoji analizi na funkciji "Sine", namesto da bi uporabili strune.

Vendar funkcija "sinusa", ki jo izražajo ti astronomi, ni danes uporabljena; Ta funkcija ni bila delež (kot je bila uporabljena danes), ampak dolžina nasprotne strani do kota pravokotnika trikotnika, katere hipotenuza je znana.

- Arabija in trigonometrične funkcije

Ob koncu osmega stoletja so arabski astronomi, na katere vplivajo trigonometrijske študije, ki sta jih izvedli narodi Grčije in Indija.

Na ta način so konec 10. stoletja vzgojili dobro znane funkcije dojk, kosinusa, tangenta, sovz, sušenja in žetve.

Odkrili so tudi in preverili primarne teoreme trigonometrije, ki se uporabljajo pri analizi ravnih in sferičnih trikotnikov. Poleg tega so arabski matematiki predlagali uporabo ene vrednosti ("1") za radio (r = 1), kar je povzročilo sodobne vrednosti trigonometričnih funkcij.

- Prispevki z zahoda

Johann Müller, znan kot Regiomontanus (1436-1476). Dosežena sistematizacija in posploševanje trigonometričnih metod, ki se uporabljajo na območju geometrije. Via: Wikimedia Commons

Na matematiko zahoda, zlasti med dvanajstim in petnajstim stoletjem, so močno vplivali postulati starodavne Grčije, Indije in Arabcev.

Vam lahko služi: chi-kvadrat (χ²): porazdelitev, kako se izračuna, primeri

V tem času so bili odločilni na območju trigonometrije-prispevki Johanna Müllerja, znanega tudi kot Regiomontanus (1436-1476). Ta matematik je dosegel sistematizacijo in posploševanje trigonometričnih metod, ki se uporabljajo na območju geometrije.

Regiomontanus je podrobneje in objavil pogodbo, ki jo je poklical Triangulis omnimodis libri, ki je bila sestavljena iz petih knjig in skupno 131 strani.

V tej knjigi je urejal vse koncepte ravne in sferične trigonometrije, ki so jih pozneje uporabljali pomembni astronomi, kot so: Nicolás Kopernic.

- Trigonometrija sedemnajsto in osemnajsto stoletje

V sedemnajstem stoletju so študije o trigonometričnih izračunih uspevale zahvaljujoč prispevkom matematikov, kot je Scotch John Napier (1550-1617), ki je vzgojil različne metode za reševanje sferičnih trikotnikov.

John Napier. Vir: Avtor Encard Samuela Freemana (1773-1857) [javna domena], prek Wikimedia Common

Kasneje, v 18. stoletju, so bili prispevki švicarskega matematika Leonharda Eulerja (1707-1783) odločilni, saj so njegove študije postavile temelje sodobne trigonometrije z uvedbo zapisa, ki se trenutno uporablja za trigonometrične funkcije.

Poleg tega je Euler uspel določiti eksponentno funkcijo in odkril svoj odnos s trigonometričnimi funkcijami, kar mu je omogočilo opis značilnosti trigonometrije.

Nato je sir Isaac Newton (1643-1727) z izumi diferencialnega in integralnega računanja olajšal predstavitev velikega števila matematičnih funkcij, med katerimi so trigonometrični. Na ta način je trigonometrija postala del matematične analize, kjer ima danes temeljno vlogo.

Ilustracija sir Isaaca Newtona

Reference

1. Mansfield, Daniel. Wildberger, n. (2017). Plimpton 322 je babilonska natančna seksualna trigonometrija. Pridobljeno 20. maja 2020 od: Schoendirect.com
2. Jimenez s. (2017). Zgodovina trigonometrije in njenih aplikacij. Pridobljeno 23. maja 2020
3. Pérez, v. (2010). Zgodovina trigonometrije. Pridobljeno 22. maja 2020 od: Laguia2000.com
4. S.Do. (s.F.) Trigonometrija. Pridobljeno 23. maja 2020 iz: Blogspot.com
5. Merlet, Jean-Pierre (2004). Opomba o zgodovini trigonometričnih funkcij. Pridobljeno 22. maja 2020 od: neto
6. Adamek, t., Penkalski, k., Valentine, g. (2005). Zgodovina trigonometrije. Pridobljeno 23. maja 2020 od: citseseerx.Ist.Psu.Edu/