Gravicentro

Kaj je davek?

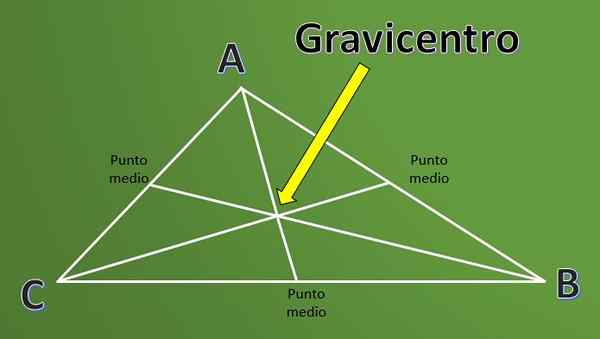
On Gravicentro To je definicija, ki se pri delu s trikotniki pogosto uporablja pri geometriji. Da bi razumeli definicijo Gravicentra, je treba najprej vedeti definicijo "medija" trikotnika.

Mediani trikotnika so linijski segmenti, ki se začnejo na vsaki točki in dosežejo sredino nasprotne strani do omenjene točke.

Točka presečišča treh medianov trikotnika se imenuje baricentro ali je znana tudi kot obdavčitev. Ni dovolj samo vedeti definicije, zanimivo je vedeti, kako se ta točka izračuna.

Izračun baricentra

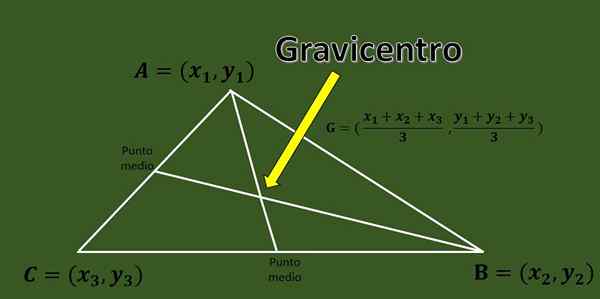
Glede na ABC trikotnik z vrhovi A = (x1, y1), b = (x2, y2) in c = (x3, y3) je gravicentro presečišče treh medianov trikotnika.

Hitra formula, ki omogoča izračun obdavčitve trikotnika, so znane koordinate njegovih točk:

G = ((x1+x2+x3)/3, (y1+y2+y3)/3).

S to formulo lahko poznate lokacijo Gravicentra v kartezijanski ravnini.

Značilnosti davka

Tri mediane trikotnika ni treba izslediti, saj bo pri risanju dveh dokazano, kje je obdavčitev.

Obdavčenje vsako mediano razdeli na 2 dela, katerih delež je 2: 1 Kaj je med točko in letakom.

Naslednja slika bolje prikazuje to lastnost.

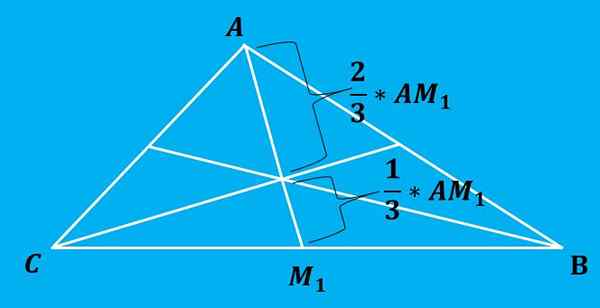
Formula za izračun obdavčitve je zelo preprosta za uporabo. Način pridobivanja te formule je z izračunom rajnih enačb, ki jih vsaka mediana določi, in nato poiščete rezalno točko teh vrstic.

Vaje

Spodaj je majhen seznam težav pri izračunu baricentra.

1.- Glede na trikotnik tokov A = (0,0), B = (1,0) in C = (1,1), izračunajte obdavčitev omenjenega trikotnika.

S pomočjo dane formule je mogoče hitro sklepati, da je Gravicentro ABC trikotnika:

G = ((0+1+1)/3, (0+0+1)/3) = (2/3, 1/3).

2.- Če ima trikotnik točke A = (0,0), B = (1,0) in C = (1/2.1), kakšne so koordinate obdavčenja?

Ker so znani točki trikotnika, se uporablja formula za izračun obdavčitve. Zato ima Gravicentro koordinate:

G = ((0+1+1/2)/3, (0+0+1)/3) = (1/2, 1/3).

3.- Izračunajte možne davkoplačevalce za enakostranični trikotnik, tako da sta dve njegovi točki A = (0,0) in B = (2,0).

V tej vaji sta določena le dve točki trikotnika. Da bi našli možne gravicente, mora najprej izračunati tretji vrhovi trikotnika.

Ker je trikotnik enakostraničen in je razdalja med A in B 2, mora biti tretja točka C na razdalji 2 od A in B.

Z uporabo dejstva, da v enakostraničnem trikotniku višina sovpada s srednjo in tudi z uporabo teorema o pitagori, je mogoče sklepati, da so možnosti za koordinate tretjega vrha C1 = (1, √3) ali C2 = (1, (1, - - - √3).

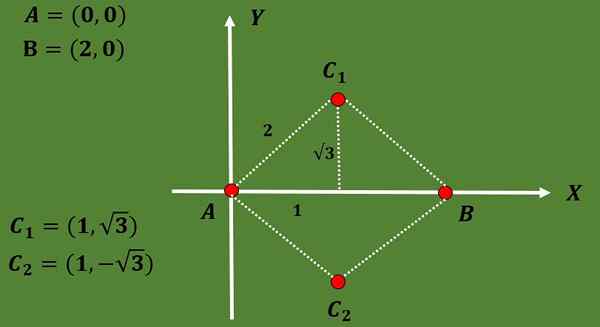
Tako da so koordinate obeh možnih gravicentrov:

G1 = ((0+2+1)/3, (0+0+√3)/3) = (3/3, √3/3) = (1, √3/3),

G2 = ((0+2+1)/3, (0+0 -√3)/3) = (3/3, -pti.

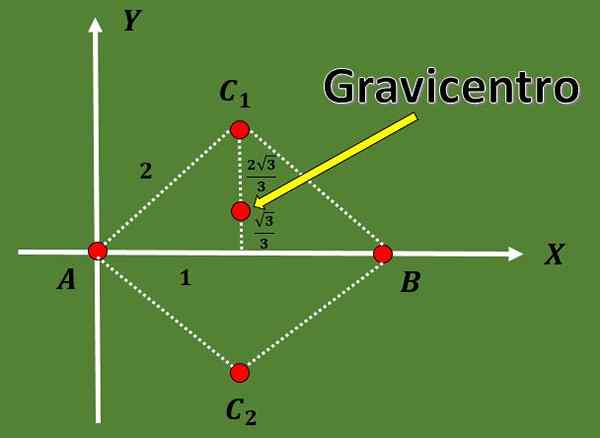
Zahvaljujoč prejšnjim računom je mogoče tudi opozoriti, da je mediana razdeljena na dva dela, katerih delež je 2: 1.