Stopnje svobode, kako jih izračunati, vrste, primeri

The Stopnje svobode V statistiki je število neodvisnih komponent naključnega vektorja. Če ima vektor n komponente in obstajajo str linearne enačbe, ki povezujejo njegove komponente, nato stopnja svobode Je n-p.

Koncept Stopnje svobode Pojavlja se tudi v teoretični mehaniki, kjer so v bruto načinu enakovredni dimenziji prostora, kjer se delček premika, razen števila ligatur.

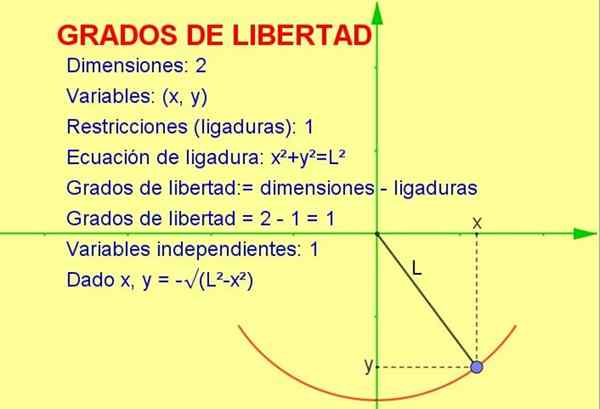
Slika 1. Nihalo se premika v dveh dimenzijah, vendar ima le nekaj svobode, ker se mora premikati v polmeru. Vir: f. Zapata.

Ta članek bo obravnaval koncept stopenj svobode, ki se uporablja za statistiko, vendar je mehanski primer lažje vizualizirati na geometrijski način.

[TOC]

Vrste stopinj svobode

Glede na kontekst, v katerem se uporablja, se lahko način izračuna števila stopenj svobode razlikuje, vendar je osnovna ideja vedno enaka: skupne dimenzije manj število omejitev.

V mehanskem primeru

Razmislite o delcu, ki niha, vezana na vrv (nihalo), ki se premika v navpični ravnini x-y (2 dimenziji). Vendar je delček dolžan premikati po obodu polmera, ki je enak dolžini vrvi.

Ker se delček lahko premika le na tej krivulji, število Stopnje svobode Je 1. To je mogoče predstaviti na sliki 1.

Način za izračun števila stopenj svobode je, da se razlikuje v številu dimenzij, razen števila omejitev:

Stopnje svobode: = 2 (dimenzije) - 1 (ligacija) = 1

Druga razlaga, ki nam omogoča, da dosežemo rezultat, je naslednja:

-Vemo, da je dva -dimenzionalna položaj predstavljena s koordinatno točko (x, y).

-Ker pa mora točka izpolniti enačbo oboda (x² + in² = L²) Za določeno vrednost spremenljivke x spremenljivko in je določena z omenjeno enačbo ali omejitvijo.

Na ta način je samo ena od spremenljivk neodvisna in sistem ima Ena (1) stopnja svobode.

Vam lahko služi: klasična verjetnost: izračun, primeri, rešene vaje

V naboru naključnih vrednosti

Za ponazoritev, kaj pomeni koncept, predpostavimo vektor

x = (x₁, x₂,…, X_n)

Predstavlja vzorec n Naključne vrednosti, ki so običajno razporejene. V tem primeru naključni vektor x ima n neodvisne komponente in zato se reče x ima n stopnje svobode.

Zdaj zgradimo vektor r odpadkov

r = (x₁ - , x₂ - ,.. ., x_n - )

Kjer predstavlja povprečje vzorca, ki se izračuna na naslednji način:

= (x₁ + x₂ +.. .+ x_n) / n

Potem vsota

(x₁ - )+(x₂ - )+.. .+(x_n - ) = (x₁ + x₂ +.. .+ x_n) - n = 0

To je enačba, ki predstavlja omejitev (ali ligacijo) v vektorskih elementih r odpadkov, saj če je znan N-1, vektorske komponente r, Enačba omejitve določa neznano komponento.

Zato vektor r dimenzije n z omejitvijo:

∑ (x_Yo - ) = 0

Ima (N - 1) Stopnje svobode.

Ponovno se uporabi, da je izračun števila stopenj svobode:

Stopnje svobode: = n (dimenzije) - 1 (omejitve) = n -1

Primeri

Variance in stopnje svobode

Variance s² Opredeljen je kot povprečje kvadrata odstopanj (ali odpadkov) vzorca podatkov:

s² = (r•r) / (N-1)

kje r je vektor odpadkov r = (x1 -, x2 -, .. ., Xn -) in debela točka (•) je operater skalarnega izdelka. Formula variance lahko zapišemo na naslednji način:

s² = ∑ (x_Yo - )² / (N-1)

Vsekakor je treba opozoriti, da je pri izračunu povprečja kvadrata odpadkov razdeljen na (N-1) in ne med N, saj kot je razpravljalo v prejšnjem razdelku, število stopenj svobode vektor r je (n-1).

Če je bil za izračun variance razdeljen med n Namesto (n-1) bi imel rezultat pristranskost, ki je zelo pomembna za vrednosti n manj kot 50.

Lahko vam služi: analitična geometrija

V literaturi se pojavlja tudi formula variance z delilnikom n namesto (n-1), ko gre za varianco populacije.

Toda niz naključnih spremenljivk odpadkov, ki jo predstavlja vektor r, Čeprav ima dimenzijo n, ima le (n-1) stopnje svobode. Če pa je številka podatkov dovolj velika (n> 500), se obe formuli zbližata na enak rezultat.

Kalkulatorji in preglednice ponujajo dve različici variance in standardni odklon (ki je kvadratni koren variance).

Naše priporočilo glede na predstavljeno analizo je, da vedno izberemo različico z (N-1) vsakič, ko je treba izračunati varianco ali standardno odstopanje, da se izognete rezultatom s pristranskostjo.

V kvadratni distribuciji Chi

Nekatere porazdelitve verjetnosti v neprekinjeni naključni spremenljivki so odvisne od parametra, imenovanega stopnja svobode, To je primer porazdelitve kvadrata chi (χ²).

Ime omenjenega parametra izhaja le iz stopenj svobode naključnega vektorja, na katerem se uporablja ta porazdelitev.

Predpostavimo, da obstajajo populacije G, od katerih se odvzamejo vzorci N velikosti:

X₁ = (x1₁, x1₂,... x1_n)

X2 = (x2₁, x2₂,... x2_n)

.. .

X_J = (xj₁, xj₂,… XJ_n)

.. .

Xg = (xg₁, Xg₂,… Xg_n)

Prebivalstvo J ki ima povprečen in standardni odklon Sj, sledite običajni porazdelitvi n (, Sj ).

Tipizirana ali normalizirana spremenljivka ZJ_Yo je opredeljen kot:

Zj_Yo = (xj_Yo - ) / Sj.

In vektor Zj Tako je opredeljeno:

Zj = (Zj₁, Zj₂,…, Zj_Yo,…, Zj_n) In sledite normalni porazdelitvi, ki je tipizirala n (0,1).

Potem spremenljivka:

Q = (Z1₁ ^2 + z2₁^2+… . + Zg₁^2),… ., (Z1_n^2 + z2_n^2+… . + Zg_n^2))

Sledite porazdelitvi χ²(g) imenovan Chi kvadratna porazdelitev s stopnjo svobode g.

V kontrastu hipoteze (z rešenim primerom)

Ko želite narediti kontrast hipoteze, ki temelji na določenem nizu naključnih podatkov, je treba vedeti Število stopenj svobode g Da lahko uporabite test s kvadratnim chi.

Vam lahko služi: neprekinjena enotna porazdelitev: značilnosti, primeri, aplikacije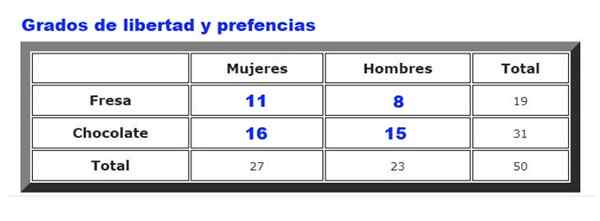 Slika 2. Ali obstaja razmerje med okusom sladoleda in spolom strank? Vir: f. Zapata.

Kot primer bodo analizirani podatki, zbrani na nastavitvah čokolade ali jagodnega sladoleda med moškimi in ženskami v neki sladoledni trgovini. Pogostost, s katero moški in ženske izberejo jagode ali čokolado, je povzeta na sliki 2.

Najprej se izračuna pričakovana tabela frekvence, ki je narejena z množenjem Skupne vrste zanj Skupni stolpci, deljeno s Skupni podatki. Rezultat je prikazan na naslednji sliki:

Slika 3. Izračun pričakovanih frekvenc na podlagi opazovanih frekvenc (modre vrednosti na sliki 2). Vir: f. Zapata.

Nato nadaljujemo z izračunom kvadrata CHI (iz podatkov) z naslednjo formulo:

χ² = ∑ (f_tudi - F_in)² / F_in

Kjer f_tudi so opažene frekvence (slika 2) in f_in so pričakovane frekvence (slika 3). Vsota je nad vsemi vrstami in stolpci, ki v našem primeru dajejo štiri izraze.

Po opravljanju operacij, ki jih dobite:

χ² = 0,2043.

Zdaj je treba primerjati s teoretičnim kvadratom, ki je odvisen od Število stopenj svobode g.

V našem primeru je ta številka določena na naslednji način:

G = (#Filas - 1) (#Columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Izkazalo se je, da je število stopenj svobode g tega primera 1.

Če želite preveriti ali zavrniti ničelno hipotezo (H0: ni povezave med okusom in spolom) s stopnjo pomena 1%, se teoretični Chi kvadrat izračuna s stopnjo svobode g = 1.

Vrednost, ki naredi nakopičeno frekvenco, je iskana (1 - 0.01) = 0.99, to je 99%. Ta vrednost (ki jo lahko dobimo iz tabel) je 6.636.

Ko teoretični chi presega izračunano, se preveri ničelna hipoteza.

Torej z zbranimi podatki ni povezave med okusom spremenljivk in spolom.

Reference

1. Minitab. Kakšne so stopnje svobode? Pridobljeno iz: Podpora.Minitab.com.
2. Moore, David. (2009) Osnovna uporabljena statistika. Urednik Antoni Bosch.
3. Leigh, Jennifer. Kako izračunati stopnje svobode v statističnih modelih. Okrevano od: Geniolandia.com
4. Wikipedija. Stopnja svobode (statistika). Okrevano od: je.Wikipedija.com
5. Wikipedija. Stopnja svobode (fizična). Okrevano od: je.Wikipedija.com