Prekomerna funkcija, lastnosti, primeri

A Prevelika funkcija To je vsak odnos, kjer je vsak element, ki pripada kodominiju, slika vsaj enega domenskega elementa. Znana tudi kot funkcija približno, So del klasifikacije funkcij glede načina povezanosti njihovih elementov.

Na primer funkcija F: a → B definirano s F (x) = 2x

Ki se bere "F to gre od Do do B definirano s F (x) = 2x "

Na dotik določite začetne in nabore prihoda A in b.

A: 1, 2, 3, 4, 5 Zdaj bodo vrednosti ali slike, ki jih bodo vsak od teh elementov sprostili, ko bodo ocenjene F, To bodo elementi kodominija.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Tako tvori niz B: 2, 4, 6, 8, 10

Nato je mogoče sklepati, da:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 definirano s F (x) = 2x je prekomerna funkcija

Vsak element kodominija mora biti vsaj eno delovanje neodvisne spremenljivke z zadevno funkcijo. Ni omejevanja slike, element kodominija je lahko podoba več elementa domene in se še naprej ukvarja z a Prevelika funkcija.

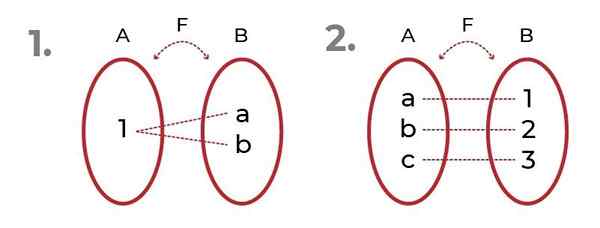
Slika prikazuje 2 primera z Obitne funkcije.

Vir: Avtor

V prvem opažamo, da se slike lahko napotijo ​​na isti element, ne da bi pri tem ogrozili Pretiranost funkcije.

V drugem vidimo pravično porazdelitev med domeno in slikami. To povzroči Bijektivna funkcija, kjer so merila Injektivna funkcija in prekomerna funkcija.

Še ena metoda za prepoznavanje Obitne funkcije, je preveriti, ali je kodominium enak rangu funkcije. To pomeni, da če je nabor prihoda enak slikam, ki jih ponuja funkcija, pri ocenjevanju neodvisne spremenljivke, Funkcija je pretirana.

[TOC]

Lastnosti

Razmisliti Pretirano Naslednje je treba izpolniti funkcijo:

Biti F: d_F → C_F

∀ B ℮ C_F  In do ℮  D_F   / F (a) = b

To je algebrski način, da to ugotovimo Za vse "B", ki spada v C_F Obstaja "A", ki pripada D_F  takšno, da je funkcija F, ocenjena v "A", enaka "B". 

Lahko vam služi: radikalne lastnosti

Prekomernost je posebnost funkcij, kjer sta kodominium in rang podobna. Tako elementi, ocenjeni v funkciji, sestavljajo nabor prihoda.

Kondicioniranje funkcij

Včasih funkcija, ki ni Pretirano, lahko podvrže določeni kondiciji. Ti novi pogoji lahko to spremenijo v Prevelika funkcija.

Vse vrste sprememb domene in kodominija funkcije so veljavne, kjer je cilj izpolniti lastnosti prekomerne poti v ustreznem razmerju.

Primeri: rešene vaje

Izpolnjevanje pogojev Pretiranost To je treba uporabiti različne tehnike kondicioniranja, da se zagotovi, da je vsak element kodominija znotraj nabora slik funkcije.

Vaja 1

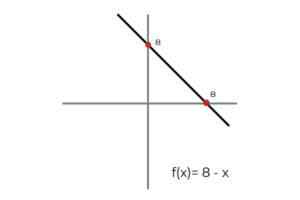
• Biti funkcija F: r → R definirana s črto F (x) = 8 - x

O: [Vse resnične številke]

Vir: Avtor

V tem primeru funkcija opisuje neprekinjeno črto, ki zajema vse realne številke tako v njihovi domeni kot v dosegu. Ker je čin funkcije R_F Je enak kodominiju R Lahko sklepamo, da:

F: r → R definirana s črto F (x) = 8 - x je Prevelika funkcija.

To velja za vse linearne funkcije (funkcije, katerih večja stopnja spremenljivke je ena).

Vaja 2

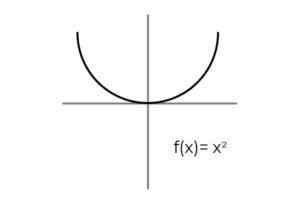
• Preučite funkcijo F: r → R definirano s F (x) = x² : Določite, če je a Prevelika funkcija. V primeru, da ni, pokažite potrebno kondicioniranje, da jo preverimo.

Vir: Avtor

Prva stvar, ki jo je treba upoštevati, je kodominium F, ki je sestavljena iz resničnih številk R. Funkcija ni možnosti, da bi metala negativno vrednost, ki izključuje negativne resnične med morebitnimi slikami.

Kondicioniranje intervalnega kodominija [0 , ∞ ]. Izogibajte se, da bi pustili elemente co -aalomio, ne da bi se povezali F.

Slike se ponavljajo za pare elementov neodvisne spremenljivke, na primer x = 1 in x = - 1.  Toda to vpliva le na Injektivnost  funkcije, ki ni problem za to študijo.

Vam lahko služi: zaporedni derivati

Na ta način je mogoče sklepati, da:

F: r  →[0, ∞ ) definirano s F (x) = x²    Je prekomerna funkcija

Vaja 3

• Določite pogoje kodominija, ki bi jih pretirano za funkcije

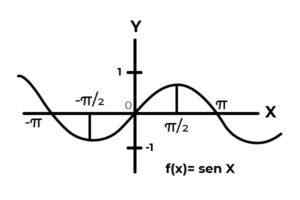
F: r  → R definirano s F (x) = greh (x)

F: r  → R definirano s F (x) = cos (x)

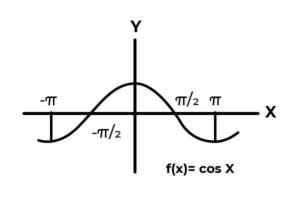Vir: Avtor Vir: Avtor.

Obnašanje trigonometričnih funkcij je podobno kot pri valovih, saj je zelo pogosto najti ponovitve odvisne spremenljivke med slikami. Tudi v večini primerov je obseg funkcije omejen na en ali več sektorjev prave črte.

To je primer sinusnih in kosinusnih funkcij. Kjer njihove vrednosti nihajo v intervalu [-1, 1]. Omenjeni interval mora pogoditi kodominium, da doseže ovojnico funkcije.

F: r  →[-eleven] definirano s F (x) = greh (x)  Je prekomerna funkcija

F: r  →[-eleven]definirano s F (x) = cos (x) Je prekomerna funkcija

Vaja 4

• Preučite funkcijo

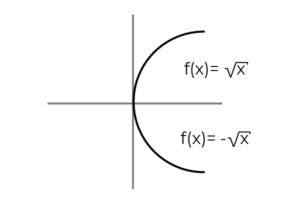
F: [0, ∞ ) → R definirano s F (x) = ± √x   označite, če je a Prevelika funkcija

Vir: Avtor

Funkcija F (x) = ± √x  Ima posebnost, ki določa 2 odvisni spremenljivki pri vsaki vrednosti "x" . To pomeni, da obseg prejme 2 elementa za vsakega, ki se izvaja v domeni. Za vsako vrednost "x" je treba preveriti pozitivno in negativno vrednost za vsako vrednost "x".

Pri opazovanju začetne sklope je ugotovljeno, da je domena že omejena, da se izognemo nedoločenim pridelanim pri oceni negativne številke znotraj korena.

Pri preverjanju območja funkcije kaže, da vsaka vrednost kodominija pripada območju.

Na ta način je mogoče sklepati, da:

F: [0, ∞ ) → R definirano s F (x) = ± √x  Je prekomerna funkcija

Vam lahko služi: sočasni vektorji: značilnosti, primeri in vaje

Vaja 4

• Preučite funkcijo F (x) = ln x  označite, če je a Prevelika funkcija. Pogoj Prihod in odhod je, da funkcijo prilagodimo kriterijem prekomernosti.

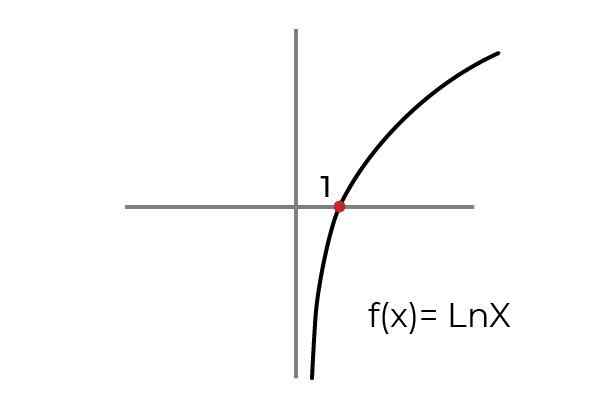Vir: Avtor

Kot je prikazano v grafu, funkcija F (x) = ln xje opredeljen za vrednosti "x", večje od ničle. Medtem ko vrednosti "in" ali slik lahko sprejmejo katero koli resnično vrednost.

Na ta način lahko omejimo domeno F (x) = do intervala (0 , ∞ )

Medtem ko se lahko uvrstitev funkcije vzdržuje kot nabor realnih številk R.

Glede na to je mogoče sklepati, da:

F: [0, ∞ ) → R definirano s F (x) = ln x  Je prekomerna funkcija

Vaja 5

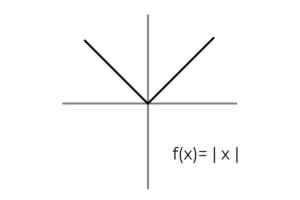
• Preučite funkcijo absolutne vrednosti F (x) = | x | in določite komplete prihoda in odhoda, ki so zbrani po merilih za alefvitost.

Vir: Avtor

Domena funkcije je izpolnjena za vse realne številke R. Na ta način je treba v kodominiju izvesti edino kondicioniranje, ob upoštevanju, da funkcija absolutne vrednosti sprejme le pozitivne vrednosti.

Kodominium funkcije je vzpostavljen, ki ga izenači na območje istega

[0 , ∞ )

Zdaj je mogoče sklepati, da:

F: [0, ∞ ) → R definirano s F (x) = | x |  Je prekomerna funkcija

Predlagane vaje

1. Preverite, ali so naslednje funkcije prekomerne:

• F: (0, ∞ ) → R definirano s F (x) = log (x + 1)
• F: r → R definirano s F (x) = x³
• F: r →[1, ∞ )  definirano s F (x) = x²  + 1
• [0, ∞ ) → R definirano s F (x) = log (2x + 3)
• F: r → R definirano s F (x) = sec x
• F: r - 0 → R definirano s F (x) = 1 / x

Reference

1. Uvod v logiko in kritično razmišljanje. Merrilee h. Losos. Univerza v Pittsburghu
2. Težave v matematični analizi. Piotr Bilar, Alfred Witkowski. Univerza v Wroclawu. Palica.
3. Elementi abstraktne analize. Mícheál o'searcoid doktorat. Oddelek za matematiko. University College Dublin, Beldfield, Dublind 4
4.  Uvod v logiko in metodologijo deduktivnih znanosti. Alfred Tarski, New York Oxford. Oxford University Press.
5.  Načela matematične analize. Enrique Linés Escardó. Uredništvo Reverté s. Do leta 1991. Barcelona, ​​Španija.