Značilnosti, primeri, primeri, vaje

The Stopenjska funkcija y = s (x) je funkcija, opredeljena v kosih ali po delih, tako da ima v končnem intervalu [a, b] končno število diskontinuitet, ki ji bomo rekli x₀ < x₁ < x₂ <… . x_n.  V vsakem odprtem intervalu (x_Yo , x_i+1) in ima konstantno vrednost vrednosti s_Yo, Z diskontinuitetami -Saltos- v točkah x_Yo.

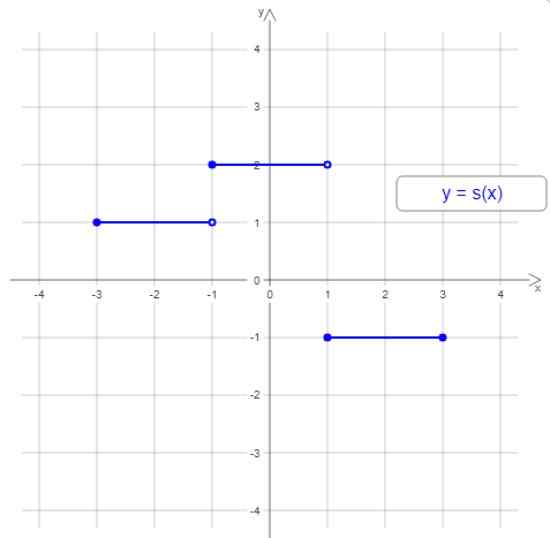
Graf, ki je posledica takšne funkcije, je sestavljen iz korakov ali korakov. Oglejmo si primer spodaj:

Slika 1. Primer stoječe funkcije. Vir: Wikimedia Commons.

Graf te stopničaste funkcije ima tri korake ali postavljene intervale, na splošno. Širina korakov je lahko drugačna in stopnišče ni vedno naraščajoče ali spuščanje.

Zadevano funkcijo primera je mogoče zapisati, ki določa širino in visoko vsakega koraka, kot je ta:

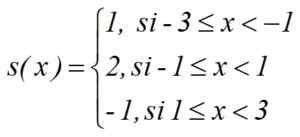
[TOC]

Značilnosti stopničaste funkcije

-Funkcija dobi svoje ime po grafu v obliki korakov, ki jih dajejo segmenti, ki ga sestavljajo. Vsak segment ima del domene funkcije in v vsaki je funkcija konstantna.

-Domena zamaknjene funkcije so vrednosti, ki spadajo v interval, za katerega je definiran: [a, b], medtem ko je obseg sestavljen z vrednosti S_Yo višine korakov.

V primeru slike 1 je domena interval [-3,3], razpon pa vrednosti -1, 1 in 2.

-Stimelna funkcija je neprekinjena, razen v vrednostih, ki omejujejo vsak korak, točke x_Yo.

-Funkcije Escalonada je mogoče dodati in pomnožiti, da vzpostavite nove stopničke.

-Njegova derivat je 0 za točke, kjer je definirana, saj je v njih funkcija konstantna. Derivat ne obstaja v prekinitvi.

-Integral stopničaste funkcije s (x) med do in b Obstaja in ustreza vsoti območij pravokotnikov širine x_Yo- x_I-1 in višina s_k, enako koraku.

Vam lahko služi: neodvisni dogodki: demonstracije, primeri, vaje

Ker je območje pravokotnika rezultat baze po višini, moramo:

Primeri zamaknjenih funkcij

Znotraj zamaknjenih funkcij obstaja več vrst, na primer funkcije cel del in funkcijo Enotni korak, kot tudi različne zamaknjene funkcije, ki opisujejo skupne situacije, kot so stopnje številnih storitev. Poglejmo nekaj primerov:

- Primer 1: Celotne stranke

Funkcija celotnega dela pogosto uporablja dvojni nosilec:

f (x) = [[x]]

In je opredeljena kot funkcija, ki vsaki realni številki dodeli najbližje ali manjše celo število, pri čemer ne upošteva katere koli decimalke, ki ima številko. Kot je primer, imamo:

Funkcija strehe ali neba

Dodeli vsaki vrednosti domene najbližje celo število s presežkom. Na primer:

[[[+2.56]] = 3

Decimalni del, ki je 0.56 in dodeljeno je najbližje celo število, ki je večje od 2.

Še en primer:

[[[-4.2]]= -3

Spet je decimalni del 0 izpuščen.2 in najvišje največje celo število bližje -4 je vredno kot vrednost -3.

Na naslednji sliki je graf stropne funkcije, upoštevajte, da je korak omejen z majhnim votlim krogom na levi in ​​en poln na desni, saj je poljubno število intervalov največje celo število dodeljeno med konci med konci med konci med konci intervala.

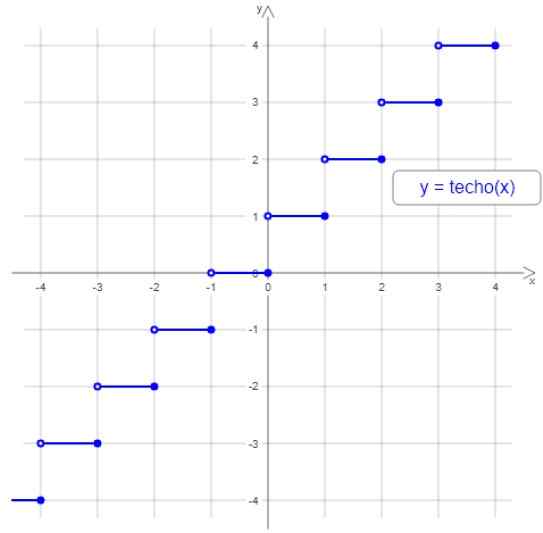Slika 2. Funkcija strehe ali neba. Vir: Wikimedia Commons.

Na primer, vse vrednosti med 3 in 4 so dodeljene celotne 4, ki sta med -2 ​​in -1 dodeljeni -1 in tako naprej.

Funkcija tal ali tal

Dodeli vsaki vrednosti domene najbližje celotno številko privzeto. Primeri te funkcije so:

Vam lahko služi: koliko desetin je v enoti?

[[+3.7]] = 3

[-1.5]] = -2

[[π]] = 3

Obe funkciji sta neprekinjeni, razen za celotne številke, kjer so predstavljeni skoki, in sta konstantna za vrednosti med cela števila K in K+1.

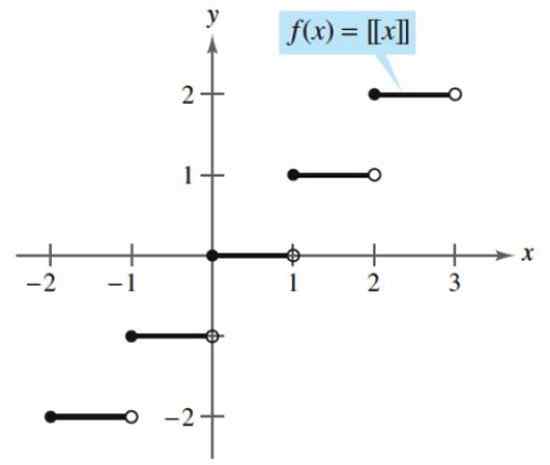Slika 3. Funkcija tal ali tal. Vir: Larson, r. Izračun spremenljivke.

- Primer 2

V mestu je taksi stopnja 3.65 USD, za prvih 100 m. In na vsakih 100 m so 0.18 USD, saj je meja na pot 50 km.

Zaželeno je vzpostaviti funkcijo, ki pot v metrih povezuje s stroški storitve z $, kar mora imeti ta obrazec:

f (x) = 3.65 + 0.18. [[x /100]] $

Kjer je lahko celotna funkcija dela neba, ki ji je dodana osnovna hitrost.65 USD. Na primer, če želimo vedeti, koliko bo plačano za potovanje 6.25 km = 6250 m, bomo imeli:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.65 USD

Če taksijska družba izbere funkcijo tal, bi stranka za potovanje plačala malo manj:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.65 USD

Rešene vaje

- Vaja 1

Klici na dolge razdalje med mesti A in B stanejo 0.40 $ 10 minut. Po tem obdobju je del ali dodatna minuta vreden 0.05 $.

Izrazite stroške c (t) klica, ki traja določeno količino minut.

Rešitev

To funkcijo lahko izrazimo, če analiziramo, kaj se zgodi z vsako možnostjo za čas klica:

Za t ≤ 10 minut

Ko je T, to je čas, ko klic traja, manj kot 10 minut, plačan 0.40 USD.

Vam lahko služi: 2 -Digit Divisions Rešene

Zato:

f (t) = 0.40 USD za t vključeno med 0 in 10 minut.

Že imamo del funkcije.

Za t> 10 minut

Entero t primer

Zdaj pa poglejmo, kaj se zgodi, ko je presežen čas t = 10 minut: lahko se zgodi, da je presežek celo število, na primer, da pogovor traja natanko 11, 12, 13, 14 minut ali več. V tem primeru bo znesek klica:

f (t) = 0.40 + 0.05 (T-10) $, za t več kot 10 minut, s celotnimi t.

To pomeni, da v tem primeru: t = 11, 12, 13, 14, 15 ... minut.

Recimo, da pogovor traja natanko 15 minut, stroški bodo:

f (15) = 0.40 + 0.05 (15-10) $ = 0.65 USD

Decimalni primer

Končno razmislite o primeru, v katerem klic traja nekaj časa z decimalnim delom. Recimo, da klic traja 15 minut in 45 sekund, kar bi bilo decimalno 15.75 minut.

Lahko ga izrazimo v smislu celotnega dela tipa tal, ob predpostavki, da želi podjetje naročniku ali nebu dati več koristi:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Poglejmo, kaj bi stranka plačala, če bi šlo za funkcijo tal:

F (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.70 USD.

Ali kot nebo funkcijo, v tem primeru bi bili stroški:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Funkcija in grafična

Kot funkcija, ki jo deli deli, je:

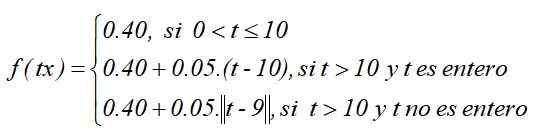
Graf funkcije bi bil tak, ob predpostavki, da je bila izbrana celotna funkcija stropa:

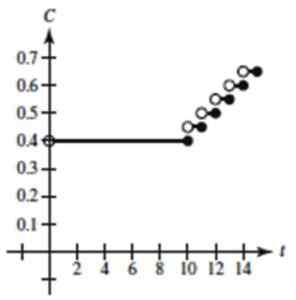Slika 4. Graf stopničaste funkcije vaje Rešena 1. Vir: Larson, r. Izračun spremenljivke.

- Vaja 2

Izračunajte integral ∫S (x) DX med -3 in 3 stopničaste funkcije:

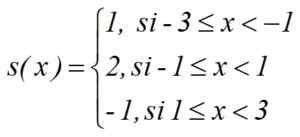
Rešitev

Uporabljamo definicijo za integral zamaknjene funkcije:

Zato je iskan integral I je:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Reference

1. Jiménez, r. 2006.Matematične funkcije. Pearson Education.
2. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
3. Matematika IV. Funkcije. Okrevano od: cobaqroo.Edu.mx.
4. Wikipedija. Celotne delovne funkcije. Okrevano od: je.Wikipedija.org.
5. Wikipedija. Stopenjska funkcija. Okrevano od: je.Wikipedija.org.