Rastoča funkcija, kako ga prepoznati, primeri, vaje

Ga imate rastoča funkcija Ko se vrednost y poveča, če se X poveča tudi v nasprotju z zmanjšanimi funkcijami, v katerih se vrednost in zmanjša, ko se x poveča.

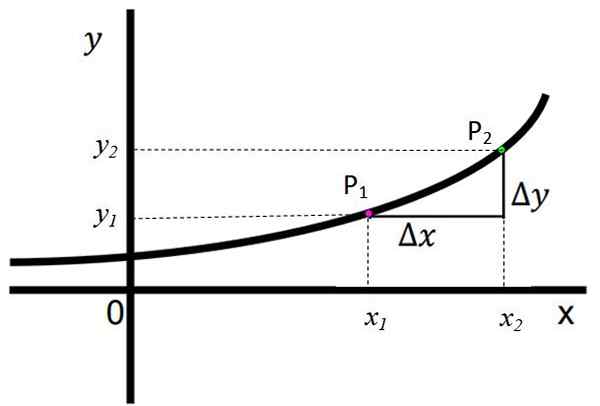
Naslednja slika prikazuje naraščajočo funkcijo in jasno je razvidno, da se pri premikanju od leve proti desni na osi X vrednost ustrezne koordinate in, enakovredna F (x), postopoma povečuje. Reče je, da če za vse x₂ > x₁, Potem obstaja in₂ > in₁.

Slika 1. Rastoča funkcija. Vir: f. Zapata.

Točke str₁ In p₂ Prikazani so, imajo oziroma koordinate (x₁, in₁) in (x₂,in₂). So opredeljeni:

Δy = y₂ -in₁

Δx = x₂ -x₁

V tej funkciji imata tako Δy kot Δx pozitiven znak, kar pomeni, da in₂ > in₁ in x₂ > x₁, oziroma. To je jasen znak, da funkcija učinkovito raste.

Dober primer vedno rastoče funkcije (povečanje monotonega) je neperijski logaritem resničnega števila. Večja kot je število, večji je njegov logaritem.

[TOC]

Kako prepoznati rastočo funkcijo?

V preprosti in neprekinjeni funkciji, kot je prikazano na sliki 1, je enostavno ugotoviti, ali se funkcija povečuje ali zmanjšuje, pod pogojem, da je graf na voljo.

Vendar lahko v nekaterih intervalih rastejo bolj zapletene funkcije in se zmanjšajo pri drugih. Zato govorimo o tem Intervali rasti in zmanjšati funkcije.

V omrežju je brezplačna spletna grafika, kot je geogebra, ki omogočajo grafikovanje vseh vrst funkcij. Če imate graf, je enostavno ugotoviti, ali se funkcija vedno povečuje, na primer f (x) = log x ali če ima intervale, v katerih raste, in druge, v katerih se zmanjšuje in kaj so.

Merilo prvega izpeljanka

Glede na določen številčni interval I, če je količina med količinami Δy in Δx pozitivna, se funkcija povečuje. In nasprotno, če je negativna, funkcija zmanjšuje.

Lahko vam služi: verjetnost frekvence: koncept, kako se izračuna in primeri

Moraš:

Δy / Δx> 0 → rastna funkcija

Dejstvo, da se Δy / Δx> 0 in funkcija v določenem intervalu povečuje interval ali celo na določeni točki vaše domene.

Dejansko je prvi derivat opredeljen kot naklon krivulje vsake točke:

Kar pomeni, da je Δx mogoče narediti čim manjše. Če je f '(x)> 0 za določeno vrednost x, na primer x = a, je naklon krivulje v tej točki f' (a) pozitiven in funkcija se bo tam povečala.

Naslednji teorem ponuja merilo za vedeti, kdaj v intervalu raste funkcija (a, b):

Teorem

Naj bo f (x) izpeljava funkcija v (a, b). Če f '(x)> 0, za katero koli vrednost x, ki pripada omenjenemu intervalu, naj bi se f (x) raste v (a, b).

Teorem se uporablja za ugotovitev, v katerih intervalih se funkcija raste, po teh korakih:

Korak 1

Poiščite točke, na katerih je f '(x) = 0, pa tudi tiste, v katerih f' (x) ne obstajajo. Te, poklicane kritične točke, To so točke, kjer lahko f '(x) spremeni zname.

2. korak

Poiščite znak f '(x) za poljubno vrednost v vsakem od intervalov, določenih s točkami, ki jih najdemo v 1. koraku.

Korak 3

Uporabite teorem, če želite vedeti, ali v vsakem intervalu funkcija raste ali ne.

Primeri rastočih funkcij

Obstajajo funkcije, ki imajo nekatere intervale rasti, druge pa zmanjšujejo, toda tiste, prikazane spodaj, vedno rastejo.

Teža glede na starost

Teža osebe, odkar se je rodila, do konca približno mladostništva, je skoraj vedno naraščajoča funkcija starosti. Dojenčki in otroci z leti rastejo in se razvijajo, nato pa, ko dosežejo odraslost, preostanek življenja pričakuje, da bodo ohranili stabilno težo, čeprav so vzponi in padci zelo pogosti.

Vam lahko služi: navpična linija

Funkcija logaritma

Funkcije resničnega spremenljivega logaritma Neperian f (x) = ln x in decimalni logaritem f (x) = log x vedno rastejo.

Funkcija kvadratne korenine realne številke

Druga funkcija, ki vedno raste, je kvadratna korenska funkcija pozitivnega resničnega števila:

y = √x

Povezana funkcija in linearna funkcija

Povezana funkcija:

f (x) = mx + b

Raste, kadar je črta pozitiven naklon. Podobno tudi identitetne in linearne funkcije:

f (x) = x in f (x) = sekira, z a> 0

Rastejo v vsej svoji domeni.

Eksponentna funkcija

Eksponentna funkcija, kot je f (x) = e^x  In na splošno funkcija obrazca:

f (x) = a^x, Z> 1

Rastejo v vsej svoji domeni.

Potencialna funkcija INPAR indeksa

Potencialne funkcije neparnega eksponenta, kot je ta:

• f (x) = x³
• g (x) = x⁵

Vedno rastejo.

Vaje

Vaja 1

Določite, v katerih intervalih se funkcija, predstavljena v naslednjem grafu, povečuje:

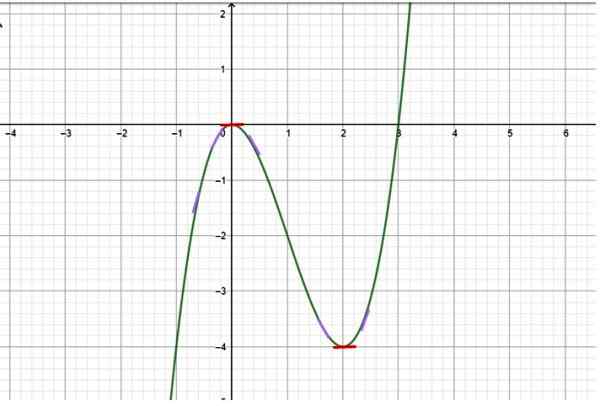Slika 2. Delovanje z intervali rasti in zmanjšanja. Vir: f. Zapata.

Rešitev

Ker je graf na voljo, je po natančnem opazovanju ugotovljeno, da ima funkcija naslednje vedenje:

-Od x → -∞ do x = 0 funkcija narašča, saj vrednosti y postanejo manj in manj negativne. Majhni segmenti naklona so bili narisani v vijolični, da se na naklonu tangentne črte na krivini označijo na različnih točkah (nagib tangenta do krivulje je natančno njegov prvi izpeljan).

Ti segmenti imajo pozitiven naklon, zato teorem zagotavlja, da funkcija v tem intervalu raste.

-Toda pri x = 0 se naklon krivulje prekliče, kar je označeno z majhnim vodoravnim rdečim segmentom. To je kritična točka funkcije.

Vam lahko služi: kaj so matematika in za kaj so namenjeni? 7 Pomembne aplikacije

Od tam se funkcija začne zmanjševati, postaja bolj negativna vrednosti in. Ta situacija se nadaljuje do x = 2, kar je še ena kritična točka.

Nato se v intervalu od x = 0 do x = 2 funkcija zmanjša.

-Od x = 2 funkcija postane vse manj negativna, dokler pri x = 3 ne prečka osi x in še naprej postane bolj pozitiven. Zato je to interval rasti.

Zaključek: Intervali rasti so (-∞, 0) in (2, ∞+), medtem ko je interval zmanjšanja (0,2).

Vaja 2

Določite intervale rasti naslednje funkcije s pomočjo meril prvega derivata:

f (x) = x² - 2x

Rešitev

Po zgoraj navedenih korakih se izračuna prvi izpeljan in enaka 0, da najdete kritične točke:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Ta vrednost določa obstoj intervalov (-nant, 1) in (1, ∞+). Izbrani sta dve poljubni vrednosti, ki pripadata vsakemu:

-Za x = 0, ki spada v (-∞, 1), morate f '(0) = 2.0 - 2 = -2. Kot je rezultat negativen, se funkcija v tem intervalu zmanjšuje.

-Za x = 3, ki pripada (1, ∞+), je prvi izpeljan vreden f '(3) = 2.3 - 2 = 4. Ker je rezultat pozitiven, je sklenjeno, da funkcija raste v tem intervalu.

Bralnik lahko izgradi izvirno funkcijo f (x) = x² - 2x na spletni grafiki za potrditev tega rezultata.

Reference

1. Ayres, f. 2000. Izračun. 5ed. MC Graw Hill.
2. Leithold, l. 1992. Izračun z analitično geometrijo. Harla, s.Do.
3. Purcell, e. J., Varberg, d., & Rigdon, s. In. (2007). Izračun. Mehika: Pearson Education.
4. Matemobile. Funkcije, raste, zmanjšuje in konstantno. Okreval od: matemovil.com
5. Requena, b. Rastoče funkcije. Okrevano od: univerzeformulas.com.
6. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.