Splošne formule kvadratne enačbe, primeri, vaje

The Splošna formula, ki je znana tudi kot formula topila V nekaterih besedilih se uporablja za reševanje enačb druge stopnje: sekira² + bx + c = 0.

V njih do, b in c So resnične številke, s pogojem do se razlikuje od 0, biti x Neznano. Nato splošna formula predstavlja čiščenje neznanega z izrazom, ki vključuje vrednosti do, b in c kot sledi:

Slika 1. Splošna formula matematike se uporablja za reševanje kvadratnih enačb. Vir: f. Zapata.

In s to formulo najdete rešitev katere koli druge stopnje ali kvadratne enačbe, pod pogojem, da omenjena rešitev obstaja.

Po zgodovinarjih je bila splošna formula že poznana starodavna babilonska matematika. Pozneje so ga prek kulturnih izmenjav prenašali na druge narode, kot so Egipčani in Grki.

Formula in njene različice so prispele v Evropo zahvaljujoč muslimanskim matematikom, ki so se naselili na Iberskem polotoku. Vendar algebrske zapise niso uporabili, ki jo trenutno uporabljamo. Ta zapis je posledica francoskega matematika in kriptografskega strokovnjaka 16. stoletja Francois VIETE.

[TOC]

Kvadratne enačbe po splošni formuli

Poglejmo, kako se pojavi splošna formula, da preverimo njegovo veljavnost. Začenši iz splošne kvadratne enačbe:

sekira² + bx + c = 0

Izvedimo v praksi nekaj preprostih algebrskih manipulacij, da dosežemo dovoljenje neznanega. Obstaja več načinov, kako to prenesti, na primer dokončanje kvadratov, kot je prikazano.

Demonstracija splošne formule

Začnemo z dodajanjem (-C) na obeh straneh enakosti:

sekira² + Bx = - c

In zdaj ga pomnoži 4a, vedno na obeh straneh enakosti, da ne bi spremenili izraza:

4² x² + 4ab x = - 4ac

Dodajanje b²:

4²⋅x² + 4ab⋅x + b² = - 4AC + B²

Namen tega je dokončati kvadratke na levi strani enakosti, ki vsebuje neznano, na ta način je njegov odmik olajšen. Tako:

Vam lahko služi: delitve 8: Kaj so in lahka razlaga

-Prvi izraz: 4² x² Je popoln kvadrat 2ax

-Zadnji, ki je b², Je popoln kvadrat B.

-In osrednji izraz je dvojni produkt 2ax in b: 2⋅2ax⋅B = 4abx

Zato imamo kvadratni binomial:

4²⋅x² + 4ab⋅x + b² = (2ax + b)²

In lahko pišemo:

(2AX + B)² = - 4AC + B²

Smo korak stran od čiščenja neznanega x:

In že pridobimo splošno formulo, ki jo poznamo:

Obstajajo drugi načini za algebraično manipuliranje s kvadratno enačbo in pridobiti ta isti rezultat.

Primeri uporabe splošne formule

Za uporabo splošne formule se vrednosti A, B in C skrbno določijo in zamenjajo v formuli. Upoštevajte simbol več manj v števcu; To kaže, da moramo upoštevati dve možnosti v zvezi z operacijo, ena z znakom + in ena z znakom -.

Kvadratna enačba ima lahko naslednje rešitve, glede na vrednost subradikalne količine, znane kot diskriminatorno:

-Da b² - 4ac> 0, kvadratna enačba ima dve resnični in različni rešitvi.

-Ko b² - 4AC = 0, enačba ima edinstveno rešitev, ki jo daje:

x = -b/2a

-Končno, če B² - 4ac < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Poglejmo nekaj primerov, v katerih je uporabljena splošna formula in opazimo, da če se kateri od koeficientov, ki spremljajo neznano. In če je neodvisni izraz tisti, ki ga ne najdemo, potem je vredno 0.

- Primer 1

Rešite naslednje kvadratne enačbe:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Odgovor na

Zapišemo koeficiente vsakega izraza: a = 6, b = 11, c = -10 in nadomestimo vrednosti v splošni formuli:

Vam lahko služi: obdavčitev

x = (-11 ± 19) /12

Rezultat vodi do naslednjih dveh resničnih rešitev:

x₁ = (-11 + 19)/12 = 8/12 = 2/3

x₂ = (-11 -19)/12 = -5/2

Odgovor b

Ponovno se določijo koeficienti: a = 3, b = -5 in c = -1. Z zamenjavo v formuli:

Za razliko od prejšnjega primera kvadratni koren 37 ni celo število, lahko pa tudi dvignemo obe rešitvi in ​​pustimo korenino ali poiščemo ustrezno decimalno vrednost s pomočjo kalkulatorja:

x₁ = (-5 + √37)/6 ≈ 0.18

x₂ = (-5 - √37)/6 ≈ - 1.85

- Primer 2

Rešite enačbo druge stopnje x² - 4x +13 = 0.

Odgovor

Kot vedno prepoznamo vrednosti koeficientov in nadomestimo splošno formulo: a = 1, b = - 4, c = 13. To vodi do:

Imamo negativno korenino, zato so rešitve te enačbe zapletene številke. Koren je mogoče izraziti v smislu Yo, the Namišljena enota:

√ (36i²) = 6i

Ker i² = -1, zato so zapletene rešitve:

x₁ = (4 + 6i)/2 = 2 + 3i

x₂ = (4 - 6i)/2 = 2 - 3i

Vaja rešena

10 m dolgo stopnišče počiva proti navpični steni, s stopalo 6 m od te stene. Stopnišče zdrsne in stopalo je ločeno 3 m več od osnove.

Poiščite navpično razdaljo, ki teče skozi vrh stopnišča.

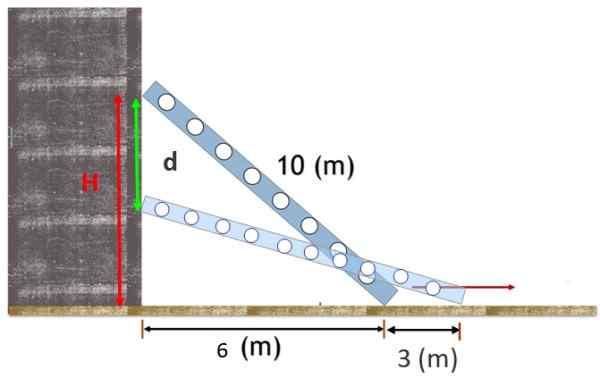Slika 2. Stopnišče, podprto na steni, se nekoliko zdrsne in zgornji zaustavitev se premika navpično navzdol na daljavo D. Vir: f. Zapata.

Rešitev

Če želite najti navpično razdaljo, ki drsi po vrhu stopnišča, morate najti položaj, v katerem je bil prvotno glede na tla. To lahko storimo s teoremom pitagore, ker je oblikovana figura tista desnega trikotnika:

H = (10² - 6²) ^½ = 8 m

Ko se stopnišče zdrsne, se razdalja premakne d, Ukrep, saj je bil vrh visok 8 m, dokler ni dosegel svojega novega položaja, na (H-D) metrih nad tlemi. Neznano, da je jasno, je D.

Vam lahko služi: nakopičena frekvenca: formula, izračun, porazdelitev, primeri

Da bi ga našli, predlagamo nov pravokotnik, ki se oblikuje po tem, ko je lestev malo zdrsnila. Ta trikotnik ima še vedno hipotenusa, ki je enaka 10 m, vzporedni cateto pa je zdaj 6m + 3m = 9 m, torej:

(H-D)² = 10² - 9² = 100 - 81 = 19

Zamenjamo h = 8m, prej izračunano:

(8-D)² = 19

Enačbo je mogoče rešiti na več načinov, vključno z uporabo splošne formule, ki jo bomo prikazali spodaj s temi koraki:

Korak 1

Razvijte opazno levo levice:

64 -16D + D² = 19

2. korak

Vzpostavite enačbo druge stopnje za neznano D:

d² - 16D + 45 = 0

Korak 3

-Koeficienti so: a = 1, b = -16 in c = 45, nadomestimo jih v splošni formuli:

Rešitve enačbe so:

d₁ = (16 + √76)/2 ≈ 12.36 m

d₂ = (16 - √76)/2 ≈ 3.64 m

4. korak

Pridobljene rešitve so analizirane: prva nima fizičnega smisla, saj lestve ni mogoče sestaviti 12.36 m, če je bil prvotno postanek visok 8 m na tleh.

Zato je pravilen odgovor druga rešitev: vrh stopnišča zdrsne d = 3.64 m.

Ali lahko bralec težavo reši z uporabo druge metode?

Reference

1. Baldor. 1977. Elementarna algebra. Venezuelske kulturne izdaje.
2. Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
3. Jiménez, r. 2008. Algebra. Dvorana Prentice.
4. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.