Absolutna frekvenčna formula, izračun, porazdelitev, primer

The Absolutna bremenitev Opredeljeno je kot številokrat, da se isti podatki ponovijo v naboru opazovanj numerične spremenljivke. Vsota vseh absolutnih frekvenc je enakovredna skupni podatki.

Kadar je veliko vrednosti statistične spremenljivke, jih je primerno pravilno organizirati, da se pridobivajo informacije o njihovem vedenju. Takšne informacije so podane z ukrepi centralne težnje in disperzijskimi ukrepi.

Slika 1. Absolutna frekvenca statističnega opazovanja je ključna za iskanje trenda, ki sledi naboru podatkov

V izračunih teh ukrepov so podatki predstavljeni s frekvenco, s katero se pojavljajo v vseh opazovanjih.

Naslednji primer prikazuje, kako je razkrivanje absolutne frekvence vsakega podatkov. V prvi polovici maja so bile to velikosti najboljših koktajlov koktajlov, dobro znanih damskih oblačil:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Koliko oblek se prodaja v določeni velikosti, na primer velikost 10? Lastnike je zainteresirano za to, da vedo naročila.

Če naročite podatke, je lažje šteti, skupaj je točno 30 opazovanj, kot je naročeno od najmanjših do najvišjih, kot je ta:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

In zdaj je očitno, da se velikost 10 ponovi 6 -krat, zato je njegova absolutna frekvenca enaka 6. Isti postopek se izvede, da se ugotovi absolutna frekvenca preostalih velikosti.

[TOC]

Formule

Absolutna frekvenca, označena kot F_Yo, Je enak številukrat kot določena vrednost x_Yo je znotraj skupine opazovanj.

Ob predpostavki, da so skupna opazovanja N vrednosti, mora biti vsota vseh absolutnih frekvenc enaka omenjenemu številu:

Vam lahko služi: papomudas

∑f_Yo = f₁ + F₂ + F₃ +… F_n = N

Druge frekvence

Če vsaka vrednost f_Yo Razdeljen je s skupnim številom podatkov n, imate relativna frekvenca F_r vrednosti x_Yo:

F_r = f_Yo / N

Relativne frekvence so vrednosti med 0 in 1, ker je n vedno večje od vseh F_Yo, Toda vsota mora biti enaka 1.

Pomnožiti za 100 do vsake vrednosti f_r imaš Relativna odstotna frekvenca, katere vsota je 100%:

Relativna odstotna frekvenca = (f_Yo / N) x 100%

Pomembno je tudi nakopičena frekvenca F_Yo Do določenega opažanja je to vsota vseh absolutnih frekvenc, dokler ne vključimo opazovanja:

F_Yo = f₁ + F₂ + F₃ +… F_Yo

Če je nakopičena frekvenca razdeljena na skupno število podatkov n, imate nakopičena relativna frekvenca, ki pomnoženo na 100 povzroči Akumuliran odstotek frekvence.

Kako dobiti absolutno frekvenco?

Če želite najti absolutno frekvenco določene vrednosti, ki spada v nabor podatkov, so vsi organizirani od najmanj do največjega in vrednost se šteje.

V primeru velikosti oblek je absolutna frekvenca velikosti 4 3 obleke, to je f₁ = 3. Za velikost 6 so bile prodane 4 obleke: f₂ = 4. V velikosti 8 4 so bile prodane, f₃ = 4 in tako naprej.

Tabela

Skupni rezultati so lahko predstavljeni v tabeli, ki prikazuje absolutne frekvence vsakega:

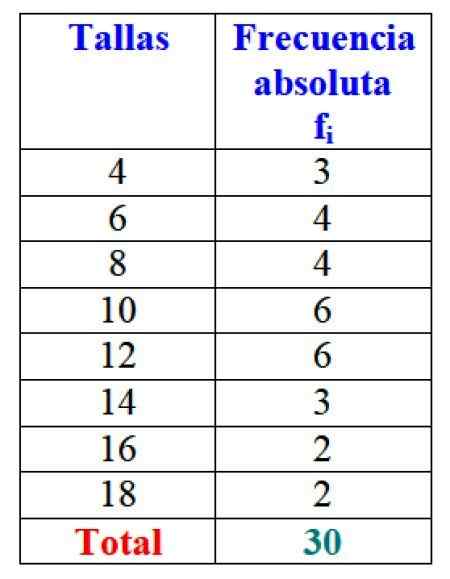Slika 2. Tabela, ki predstavlja spremenljivko "prodane prodaje" in ustrezne absolutne frekvence. Vir: f. Zapata.

Očitno je koristno naročiti informacije in biti sposoben dostopati do njih, namesto da bi delal z ohlapnimi podatki.

Pomembno: Upoštevajte, da z dodajanjem vseh vrednosti stolpca F_Yo  Skupno število podatkov je vedno pridobljeno. Če ne, je treba pregledati računovodstvo, saj obstaja napaka.

Tabela podaljšane frekvence

Prejsko tabelo lahko podaljšate tako, da dodate druge vrste frekvence v zaporednih stolpcih na desno:

Vam lahko služi: homocedastičnost: kaj je, pomen in primeri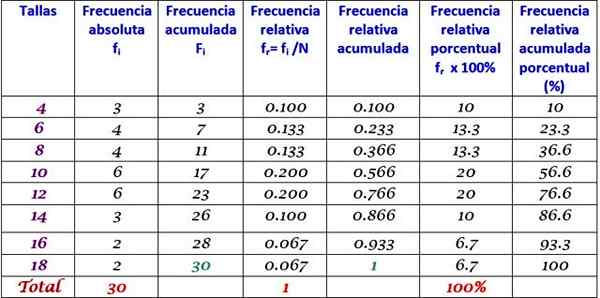

Porazdelitev frekvence

Porazdelitev frekvence je rezultat organizacije podatkov glede na njihove frekvence. Pri delu s številnimi podatki jih je priročno razvrstiti v kategorije, intervale ali razrede, vsaka z ustreznimi frekvencami: absolutno, relativno, nakopičeno in odstotek.

Cilj jih je lažje dostopati do informacij, ki jih podatki vsebujejo, in jih pravilno razlagati, kar ni mogoče, če so predstavljeni brez vrstnega reda.

V primeru velikosti podatki niso razvrščeni, saj niso preveč velikosti in jih je mogoče enostavno manipulirati in prešteti. Kvalitativne spremenljivke je mogoče delovati tudi na ta način, toda ko so podatki zelo številni, jih bolje razvrščajo v razrede.

Frekvenčna porazdelitev za združene podatke

Če želite razvrstiti podatke v razrede enake velikosti, je treba upoštevati naslednje:

-Velikost, širina ali amplituda razreda: Je razlika med največjo vrednostjo razreda in mladoletnico.

Velikost razreda se določi tako, da se razpon R deli s številom razredov, ki jih je treba upoštevati. Razpon je razlika med največjo vrednostjo podatkov in mladoletnikom, kot je ta:

Velikost razreda = obseg / število razredov.

-Omejitev razreda: interval, ki sega od spodnje meje do zgornje meje razreda.

-Blagovna znamka razreda: To je srednja točka intervala, ki velja za reprezentativno za razred. Izračuna se s pol -limitom zgornje meje in spodnjo mejo razreda.

-Število razredov: Sturges Formula je mogoče uporabiti:

Razredi = 1 + 3.322 dnevnik n

Kjer je n število razredov. Kot je običajno decimalna številka, je naslednje zaokroženo.

Primer

Velik tovarniški stroj ne deluje, saj ima ponavljajoče se napake. Zabeležena obdobja neaktivnosti v nekaj minutah omenjenega stroja so zabeležena spodaj, skupaj s 100 podatki:

Lahko vam služi: verjetnost frekvence: koncept, kako se izračuna in primeri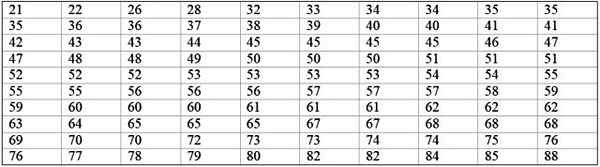

Najprej je določeno število razredov:

Razredi = 1 + 3,322 dnevnik n = 1 + 3.32 dnevnik 100 = 7.64 ≈ 8

Velikost razreda = obseg / število razredov = (88-21) / 8 = 8.375

Je tudi decimalna številka, zato traja 9 kot velikost razreda.

Blagovna znamka je povprečje med zgornjo in spodnjo mejo razreda, na primer za razred [20-29) Obstaja oznaka:

Blagovna znamka razreda = (29 + 20) / 2 = 24.5

Nadaljujte na enak način, da poiščete razredne blagovne znamke preostalih intervalov.

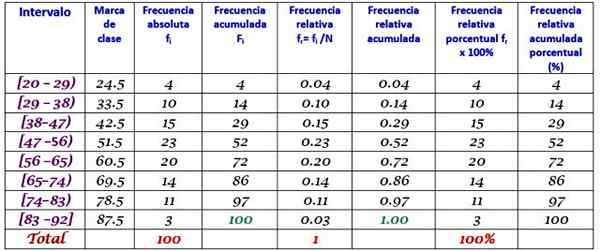
Vaja rešena

40 mladih je navedlo, da je bil čas v nekaj minutah, ki so minile po internetu prejšnjo nedeljo, naslednje, vse pogosteje naročili:

0; 12; dvajset; 35; 35; 38; 40; Štiri. Pet; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Zahteva se, da sestavi frekvenčno porazdelitev teh podatkov.

Rešitev

Ranka r niza n = 40 podatkov je:

R = 220 - 0 = 220

Uporaba formule Sturges za določitev števila razredov daje naslednji rezultat:

Razredi = 1 + 3,322 dnevnik n = 1 + 3.32 dnevnik 40 = 6.3

Kot je decimalna, je neposredna celota 7, zato so podatki razvrščeni v 7 razredov. Vsak razred ima širino:

Velikost razreda = obseg / število razredov = 220/7 = 31.4

Tesna in okrogla vrednost je 35, zato je izbrana širina razreda 35.

Oznake razredov se izračunajo v povprečju zgornje in spodnje meje vsakega intervala, na primer za interval [0,35):

Blagovna znamka razreda = (0+35)/2 = 17.5

Na enak način nadaljujemo s preostalimi razredi.

Končno se frekvence izračunajo v skladu z zgoraj opisanim postopkom, kar ima za posledico naslednjo porazdelitev:

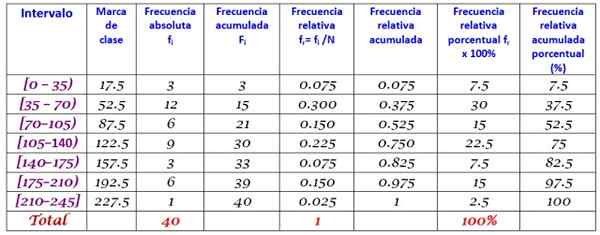
Reference

1. Berenson, m. 1985. Statistični podatki za upravo in ekonomijo. Interameriški s.Do.
2. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
3. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
4. Spiegel, m. 2009. Statistika. Serija Schaum. 4 ta. Izdaja. McGraw Hill.
5. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.