Vrednotenje funkcij

Če želite oceniti funkcijo, katere diagram je znan, je za določeno vrednost ali element začetnega niza dovolj, da opazujemo ustrezen element v naboru prihoda. Vir: f. Zapata.

Kakšna je ocena funkcij?

The Vrednotenje funkcij Sestavljen je za določitev slike določene vrednosti domene. Z drugimi besedami, za določeno vrednost začetnega niza morate v naboru prihoda najti njegovo ustrezno.

Funkcija je lahko predstavljena na več načinov. Če je na primer na voljo Vennov diagram, je ocena zelo preprosta, dovolj je, da izberete element začetnega ali domenskega nabora in si oglejte element, ki ustreza naboru prihoda.

V "…… je kapitalski diagram ...", predstavljen zgoraj, pri ocenjevanju te funkcije v elementu "Kanada" je to element "Ottawa", v primeru, da to počnete z "Mehiko", je "Mexico City" in Torej naprej.

Če je funkcija podana v obliki urejenih parov, je tudi ocena preprosta: drugi član urejenega navora je slika prvega člana. Na primer, s funkcijo f (x), opisano z:

f (x) = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Pri ocenjevanju funkcije za vrednost 3 je rezultat 6; Pri ocenjevanju 5 je 10 in tako naprej.

Prav tako lahko funkcijo ocenimo, ko je na voljo graf, pod pogojem, da se v njej prikaže vrednost, ki jo želite oceniti.

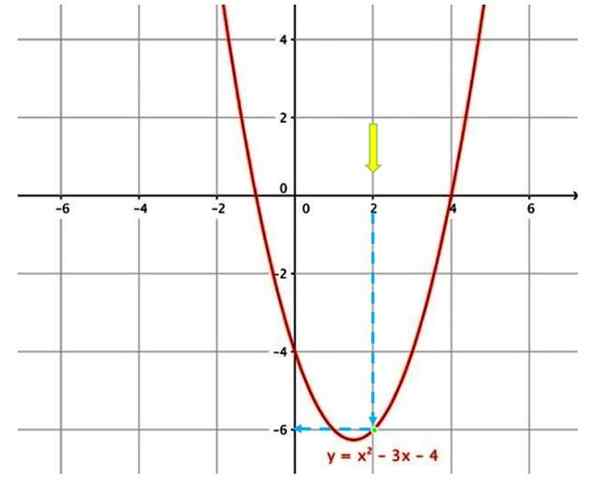Graf za oceno funkcije

Na primer, za oceno zgoraj prikazane funkcije pri x = 2 je prva stvar, ki jo poiščete v grafu x = 2 (rumena puščica).

Nato se morate premakniti po modri navpični puščici, dokler se ne dotaknete krivulje (zelena točka). Ponovno sledite modri puščici, ki označuje ustrezno vrednost na navpični osi, torej pri ocenjevanju funkcije pri x = 2, y = −6.

Lahko vam služi: trigonometrične funkcije: Osnovne, v kartezijanski ravnini, primeri, vadba

Ocenite določeno funkcijo v matematični zapisu

V spodnjem delu zgornjega grafa se pojavi grafična funkcija, vendar dana v matematični zapisu, torej skozi formulo:

f (x) = x² - 3x - 4

Ko želite oceniti funkcijo v kateri koli vrednosti x = a, morate najti f (a), ki se preprosto bere "f a".

Če želite najti rezultat, se x = a nadomesti v formuli funkcije, zahtevane operacije in izračuni pa se izvajajo.

Recimo, da želite oceniti funkcijo primera pri x = −1. To pomeni, da je treba najti F (−1).

Prvi korak je nadomestiti x = -1 v funkciji:

f (−1) = (−1)² - 3 ∙ (−1) - 4

In nato izvedite navedene operacije, ki so v tem primeru:

• Poiščite kvadrat −1: (−1)² = 1
• Odštejte prejšnjo vrednost izdelka 3 ∙ (−1): 3 ∙ (−1) = −3
• Iz prejšnjega rezultata odštejte 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

Bralec lahko potrdi ta rezultat iz grafa funkcije.

Opisani postopek se lahko uporabi za oceno funkcije na kateri koli drugi vrednosti domene. Na primer, najdete F (-2), F (100) ali celo f (h), kjer je H poljubna spremenljiva vrednost, ki spada v domeno funkcije.

Ocenite funkcijo na vrednosti x = h 

Recimo, da želite funkcijo oceniti na neki poljubni vrednosti, pogosto operacijo matematičnega izračuna.

V tem primeru se X nadomesti s H, na enak način, kot se naredi, ko X vzame poljubno številčno vrednost, rezultat pa je čim bolj poenostavljen.

Kadar nastalega delovanja ni več mogoče poenostaviti, je posledična operacija ostala.

Lahko vam služi: Enegon: Lastnosti, kako narediti enegon, primeri

Primer

Želite oceniti funkcijo f (x) = x² - 3x - 4 pri x = H+1. Potreben pristop je naslednji:

f (H+1) = (H+1)² - 3 ∙ (H+1) - 4

Na pravico do enakosti je prvi izraz izjemen izdelek:

(H+1)² = h² +2H + 1

Naslednji izraz se reši s pomočjo distribucijske lastnosti:

3 ∙ (H + 1) = 3H + 3

Ko zamenjate vse zgoraj navedeno, imate:

f (H+1) = (H+1)² - 3 ∙ (H+1) - 4 = H² +2H + 1 - (3H + 3) - 4

Podobni izrazi se zmanjšajo z algebrsko vsoto:

f (H+1) = H² + 2H + 1 - 3H - 3 - 4 = H² - H - 6

Diferencialni količnik

Diferencialni količnik ali razmerje razlik d funkcije f (x) je opredeljeno kot:

S pogojem H ≠ 0, kar je potrebno, saj delitev z 0 ni definirana.

Ta količnik se geometrično razlaga kot naklon sekanske črte do krivulje, to je črta, ki prehaja skozi dve točki. Koordinate teh točk so: [x, f (x)] in [x+h; f (x+h)], kot je razvidno iz naslednje slike:

Diferencialni količnik je enakovreden izračunu naklona sekanske črte na krivuljo, ki poteka skozi navedene točke. Vir: Wikimedia Commons.

Zato se ta količnik pojavi v izračunu derivata funkcije, saj se "H" približa vrednosti 0, sesanska črta ponavadi postane tangentna črta v točki (x, y), ker točke v presečišču preseka Slika je tako blizu, da se nagibajo k isti točki.

Tako črta postane tangentna (prestreže krivuljo v eni točki).

Prav to je definicija izpeljane iz funkcije: naklon črte tangente na krivuljo v koordinatni točki (x, f (x))).

Lahko vam služi: tehtani mediji: kako se izračuna, primeri in vaje

Kot je razvidno, diferencialni količnik zahteva oceno funkcije v (x + h) in v x. Naslednji primeri ponazarjajo, kako to storiti.

Primer 1

Želite najti diferencialni količnik funkcije f (x) = 2x - 3. Prvi korak je zvišanje ocene funkcije za x = x + h, kot je ta:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2H - 3

Nato je rezultat nadomeščen v definiciji D, ki je bil prej naveden:

S h ≠ 0.

Števec je poenostavljen, kolikor je mogoče, in zmanjšuje podobne izraze:

Končno so poenostavljeni pogosti dejavniki v štetju in imenovalcu:

D = 2

Primer 2

Poiščite diferencialni količnik funkcije f (x) = x² - 3x - 4.

Nadaljujemo kot v prejšnjem primeru in najdemo First F (x+h), pri čemer nadomestimo rezultat v D in poenostavimo na maksimum:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2HX + H² - 3x - 3H - 4

= 2x+H-3

Zato:

D = 2x+H-3

Kjer je h ≠ 0.

Rešene vaje

Vaja 1

Ocenite funkcijo f (x) = 2x² - 4x + 1, ko:

a) x = -1
b) x = 0
c) x = 2

Rešitev

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Rešitev b

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Rešitev c

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Vaja 2

Konservatorska ekipa je ugotovila, da je funkcija w (t) = 0.Lt² + 1.8T služi za modeliranje količine odpadkov "W" v kilogramih, ki jih vržemo v določeno reko, v času "t", dano v dneh.

Izračunajte količino odpadkov, vrženih v reko na koncu:

a) 3 dni
b) 1 teden
c) 1 mesec

Rešitev

Funkcija w (t) se oceni pri t = 3 dni:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kilogrami

Rešitev b

Pred oceno morate preživeti 1 teden do dni:

1 teden = 7 dni

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kilogramov

Rešitev c

Ponovno je treba spremeniti mesece v dneve:

1 mesec = 30 dni

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilogramov

Reference

1. Larson, r. 2012. Prekalenkulacija. 8. Izdaja. Cengage učenje.
2. Inštitut Monterey. Ocenjevanje funkcij. Okreval od: montereyinstitute.org.
3. Stewart, J. 2007. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
4. Sullivan, m. 1997. Prekalenkulacija. 4. Izdaja. Pearson Education.
5. Zill, d. 2008. Predhod z napredkom izračuna. 4. Izdaja. McGraw Hill.