Standardna ocena napaka, kako izračunani, primeri, vaje

On Standardna napaka ocenjevanja Izmerite odstopanje v vzorčni populacijski vrednosti. To pomeni, da standardna ocena napake meri možne spremembe povprečne vrednosti vzorca glede na resnično vrednost povprečja populacije.

Na primer, če želite vedeti povprečno starost prebivalstva države (pomeni prebivalstvo), se vzame majhna skupina prebivalcev, ki ji bomo rekli "oddaje". Iz nje se izvleče povprečna starost (srednja vrednost vzorca) in domneva se, da ima populacija povprečno starost s standardno oceno napake, ki se bolj ali manj spreminja.

M. W. Toews [cc do 2.5 (https: // creativeCommons.Org/licence/by/2.5)]

Treba je opozoriti, da je pomembno, da standardnega odklona ne zamenjujete s standardno napako in standardno oceno napake:

1- Standardni odklon je merilo disperzije podatkov; to pomeni, da je merilo spremenljivosti prebivalstva.

2- Standardna napaka je merilo spremenljivosti vzorca, izračunano na podlagi standardnega odklona populacije.

3- Standardna napaka ocenjevanja je merilo napake, ki je narejena pri jemanju vzorca kot ocena povprečne populacije.

[TOC]

Kako se izračuna?

Standardno oceno napake je mogoče izračunati za vse ukrepe, pridobljene v vzorcih (na primer standardna povprečna napaka ocene ali standardna napaka pri oceni standardne odstopanja) in meri napako, ki je narejena pri oceni resničnega populacijskega ukrepa iz njegove vrednosti vzorca

Iz standardne napake ocenjevanja je vgrajen interval zaupanja ustreznega ukrepa.

Vam lahko služi: Reverse Matrix: izračun in reševanje vadbe

Splošna struktura formule za standardno oceno napake je naslednja:

Standardna napaka ocene = ± koeficient zaupanja * Standardna napaka

Koeficient zaupanja = mejna vrednost vzorčne statistične ali vzorčne porazdelitve (normalen ali Gauss Bell, študent T, med drugim) za določen interval verjetnosti.

Standardna napaka = standardni odklon populacije, deljeno s kvadratnim korenom velikosti vzorca.

Koeficient zaupanja kaže na količino standardnih napak, ki so pripravljene dodati in odšteti prilagojene, da imajo določeno raven zaupanja v rezultate.

Primeri izračuna

Predpostavimo, da poskušate oceniti delež ljudi v populaciji, ki imajo vedenje A, in želite imeti 95 -odstotno zaupanje v njihove rezultate.

Vzemimo vzorec N ljudi in določen je delež vzorca P in njegovo dopolnilo Q.

Standardna napaka v oceni (EEE) = ± koeficient zaupanja * Standardna napaka

Koeficient zaupanja = z = 1.96.

Standardna napaka = kvadratni koren razloga med produktom vzorčnega deleža za njegovo dopolnilo in velikostjo vzorca n.

Iz standardne napake ocene, intervala, v katerem je delež populacije ali vzorčnega deleža drugih vzorcev, ki jih je mogoče oblikovati iz te populacije, z 95 -odstotno stopnjo zaupanja:

P -EEEE ≤ delež prebivalstva ≤ p + eee

Rešene vaje

Vaja 1

1- Predpostavite, da poskušate oceniti delež ljudi v populaciji, ki imajo prednost pred obogateno mlečno formulo, in želite imeti 95-odstotno zaupanje v njihove rezultate.

Vam lahko služi: sintetična delitev

Vzeti je vzorec 800 ljudi in ugotovljeno je, da ima 560 ljudi v vzorcu prednost pred obogateno mlečno formulo. Določite interval, v katerem je mogoče pričakovati delež populacije, in delež drugih vzorcev, ki jih je mogoče odvzeti iz populacije, z 95 -odstotnim zaupanjem

a) Izračunamo delež vzorca P in njegovo dopolnilo:

P = 560/800 = 0.70

Q = 1 -p = 1 -0.70 = 0.30

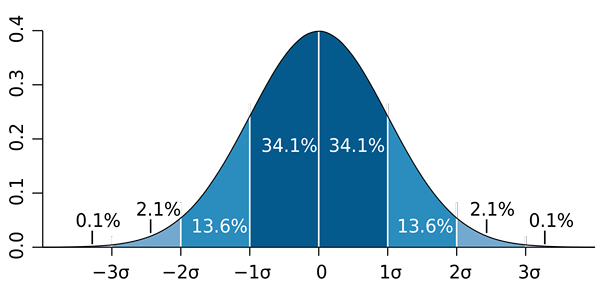
b) Znano je, da se proporcija približa normalni porazdelitvi z vzorci velike velikosti (večje od 30). Nato se uporablja tako imenovano pravilo 68 - 95 - 99.7 in moraš:

Koeficient zaupanja = z = 1.96

Standardna napaka = √ (p*q/n)

Standardna napaka ocenjevanja (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) Iz standardne napake v oceni se določi interval, v katerem se pričakuje delež populacije z 95 -odstotno stopnjo zaupanja:

0.70 -0.0318 ≤ delež prebivalstva ≤ 0.70 + 0.0318

0.6682 ≤ delež prebivalstva ≤ 0.7318

Pričakujete lahko, da se bo 70 -odstotni delež vzorca spremenil do 3.18 odstotnih točk Če je potreben drugačen vzorec 800 posameznikov ali da je dejanski delež populacije med 70 - 3.18 = 66.82% in 70 + 3.18 = 73.18%.

Vaja 2

2- Vzeli bomo od Spiegel in Stephens, 2008, naslednja študija primera:

Od skupnih ocen matematike prvih študentov univerze je bil odvzet naključni vzorec 50 kvalifikacij, v katerih je bilo najdeno 75 točk in standardno odklon, 10 točk. Kakšne so 95 -odstotne meje zaupanja za oceno povprečja kvalifikacij matematike univerze?

Lahko vam služi: kakšen je odnos med območjem Rhombusa in pravokotnikom?

a) Izračunamo standardno napako ocene:

95 -odstotni koeficient zaupanja = z = 1.96

Standardna napaka = s/√n

Standardna napaka ocenjevanja (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) Iz standardne ocene napake se vzpostavi interval, v katerem je populacija ali povprečje drugega vzorca 50, z 95 -odstotno stopnjo zaupanja:

50 -2.7718 ≤ povprečje prebivalstva ≤ 50 + 2.7718

47.2282 ≤ povprečje prebivalstva ≤ 52.7718

c) Pričakujete lahko, da se bo povprečje vzorca spremenilo do 2.7718 točk Če se vzame drugačen vzorec 50 ocen ali da je resnično povprečje ocen matematike populacije univerze med 47.2282 točk in 52.7718 točk.

Reference

1. Abraira, v. (2002). Standardni odklon in standardna napaka. Revija Semergen. Splet je bil obnovljen.Arhiv.org.
2. Rumsey, d. (2007). Vmesni statistični podatki za lutke. Wiley Publishing, Inc.
3. Salinas, h. (2010). Statistika in verjetnosti. Okreval z mat.Uda.Cl.
4. Sokal, r.; Rohlf, f. (2000). Biometrija. Načela in praksa statistike v bioloških raziskavah. Tretji ed. Blume Editions.
5. Spiegel, m.; Stephens, l. (2008). Statistika. Četrti Ed. McGraw-Hill/Medamerican iz Mehike S. Do.
6. Wikipedija. (2019). 68-95-99.7 pravilo. Pridobljeno iz.Wikipedija.org.
7. Wikipedija. (2019). Standardna napaka. Pridobljeno iz.Wikipedija.org.