Enegonske lastnosti, kako narediti enegon, primeri

A Enegon To je poligon devetih strani in devet vrhov, ki so lahko redne ali ne. Enegonsko poimenovanje prihaja iz grščine in je sestavljeno iz grških besed Ennea (devet in Gonon (kot).

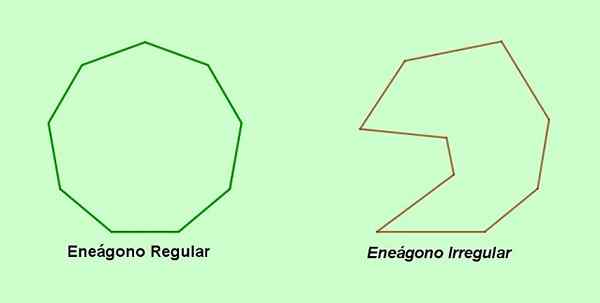
Alternativno ime za devet -stranski poligon je ne -besedna beseda, ki izvira iz latinščine nonus (devet in Gonon (Vertex). Po drugi strani pa, če so strani ali koti Enegona med seboj neenakomerne Nepravilen Enegon. Če so nasprotno, devet strani in devet kotov Enegona so enaki, potem je to a Redni Enegon.

Slika 1. Redni Enegon in nepravilen Enegon. (Lastna izdelava)

[TOC]

Enegonske lastnosti

Za poligon n strani je vsota njegovih notranjih kotov:

(N - 2) * 180 °

V Enegonu bi bilo n = 9, zato je vsota njegovih notranjih kotov:

SA = (9 - 2) * 180º = 7 * 180º = 1260 °

V katerem koli poligonu je število diagonalov:

D = n (n - 3) / 2 in v primeru Enegona, kot n = 9, morate d = 27.

Redni Enegon

V Enegonu ali rednem nonagonu.

Nato je treba meriti notranje kote Enegona 1260 ° / 9 = 140 °.

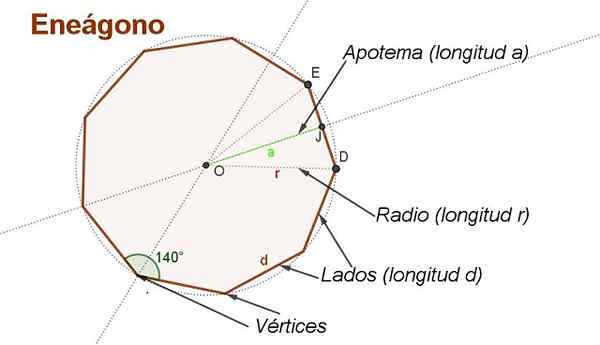Slika 2. Apothem, radio, strani, koti in vrhovi običajnega Enegona. (Lastna izdelava)

Sklepati formulo območja navadnega Enegona na strani d Priročno je narediti nekatere pomožne konstrukcije, kot so tiste, prikazane na sliki 2.

Center je Tudi Risanje mediatric dveh sosednjih strani. Center Tudi Equidista tokov.

Polmer dolžine r To je segment, ki sega iz središča Tudi Na tolici Enegona. Radijski sprejemniki so prikazani na sliki 2 Od in Oe dolžine r.

Vam lahko služi: simetrija

Apotem je segment, ki sega od središča do sredine točke na eni strani Enegona. Na primer Oj Je apotem, katerega dolžina je do.

Območje znane strani Enegona in apotema

Upoštevamo trikotnik Ode Na sliki 2. Območje tega trikotnika je produkt njegove baze Od po višini Oj deljeno z 2:

Območje Ode = (Iz * oj) / 2 = (D * a) / 2

Ker je v Enegonu 9 trikotnikov istega območja, se potem sklepa, da je območje istega:

Območje Enegona = (9/2) (d * a)

Območje znanega Enegona

Če je znana le dolžina Enegona, je treba najti dolžino apotema, da lahko uporabimo formulo prejšnjega razdelka.

Upoštevamo trikotnik Oje Pravokotnik v J (Glej sliko 2). Če se uporabi trigonometrična razmerja navora, se dobi:

tako (∡Oej) = Oj / Npr.

Kot ∡oej = 140 ° / 2 = 70 °, za bivanje EO Bisektor notranjega kota Enegona.

Poleg tega, Oj Je apotem dolžine do.

Potem kot J Je sredi točke Ed Sledi, da Ex = d/2.

Zamenjava zgornjih vrednosti v razmerju tangenta je:

Tan (70 °) = A / (d / 2).

Zdaj očistimo dolžino apotema:

A = (d/2) Porjavelo (70 °).

Prejšnji rezultat se nadomesti v formuli območja, da dobimo:

Območje Enegona = (9/2) (d * a) = (9/2)( D * (D/2) Porjavelo (70 °))

Končno obstaja formula, ki omogoča pridobitev običajnega območja Enegona, če je znana le dolžina d njegovih strani:

Območje Enegona = (9/4) d² Tan (70 °) = 6.1818 D²

Obod navadnega Enegona je poznal svojo stran

Obod poligona je vsota njegovih strani. V primeru Enegona, tako kot vsaka od strani, meri dolžino d, Njen obod bo devetkrat vsota d, to pomeni:

Vam lahko služi: polinomne enačbe

Obod = 9 d

Obod enegona je poznal svoj radio

Glede na trikotnik Oje Pravokotnik v J (Glej sliko 2), uporabi se trigonometrični razlog:

cos (∡Oej) = Npr / Oe = (d / 2) / r

Kje ste dobili:

D = 2r cos (70 °)

Če nadomestimo ta rezultat, se formula oboda dobi kot funkcija polmera Enegona:

Obod = 9 d = 18 r cos (70 °) = 6.1564 r

Kako narediti redni enegon

1- Za gradnjo rednega Enegona s pravilom in kompasom temelji na obodu c ki omejuje Enegon. (Glej sliko 3)

2- dve pravokotni črti sta narisani skozi središče ali obod. Nato sta križišča A in B ene od črt označena z obodom.

3- S kompasom, ki je v prestrezanju B in odpiranju enaka polmeru.

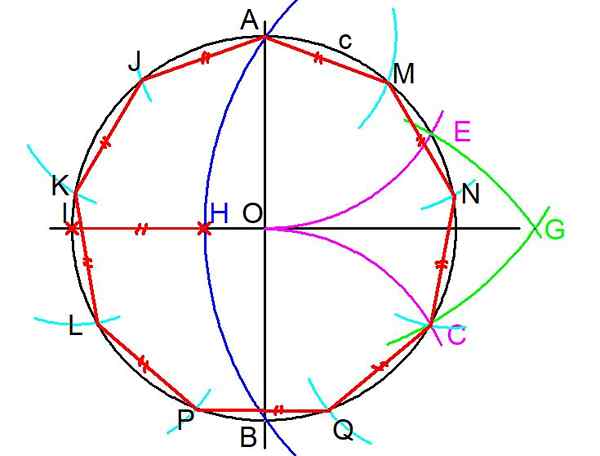Slika 3. Koraki za izgradnjo rednega Enegona. (Lastna izdelava)

4- Prejšnji korak se ponovi, vendar je narisano središče v A in Radio Ao A lok, ki prestreže na obod C v točki E.

5- Z AC odprtino in središčem v obodu je narisano. Podobno je z otvoritvijo in Center B je narisan še en lok. Presečišče teh dveh lokov je označeno kot g.

6-izdelava središča v G in z odpiranjem GA je narisan lok, ki prestreže sekundarno osi (v tem primeru vodoravno) v točki H. Presečišče sekundarne osi je označeno s prvotnim obodom C kot jaz.

7- Dolžina segmenta IH je enaka dolžini D na strani Enegona.

8- Z odpiranjem kompasa IH = D Sredinski loki zaporedno pritegnejo na radio AJ, Centro J Radio AK, KL Radio KL in Centro L Radio LP.

Lahko vam služi: linearne transformacije: lastnosti, kakšne so uporaba, tipi, primeri

9- Podobno, ki se začne z A in na desni strani, se na prvotnih obodnih točkah C točka.

10- Končno segmenti AJ, JK, KL, LP, AM, MN, NC, CQ in končno PB so narisani.

Treba je opozoriti, da metoda gradnje ni povsem natančna, saj je mogoče preveriti, da je zadnja stran PB 0,7% daljša od drugih strani. Do danes načina gradnje in gradnje kompasa ni znan, da je 100% natančen.

Primeri

Nekaj ​​primerov rešenih bo obravnavano spodaj.

Primer 1

Želite zgraditi navaden Enegon, katerega strani merijo 2 cm. Kakšen radio naj ima obseg, ki ga omeji, tako da se pri uporabi predhodno opisane konstrukcije dobi želeni rezultat?

Rešitev:

V prejšnjem razdelku je bila sklenjena formula, ki povezuje polmer r opisanega oboda z rednim degonom D:

D = 2r cos (70 °)

Čiščenje r iz prejšnjega izraza imamo:

R = d / (2 cos (70 °)) = 1.4619 * d

Nadomeščanje vrednosti d = 2 cm v prejšnji formuli A 2,92 cm polmer.

Primer 2

Koliko je območje običajnega 2 cm strani Enegon?

Rešitev:

Če želite odgovoriti na to vprašanje, se morate sklicevati na prej prikazano formulo, ki vam omogoča, da najdete območje Enegona, ki je znano dolžino D na njegovi strani:

Območje Enegona = (9/4) d² Tan (70 °) = 6.1818 D²

Zamenjava D za svojo vrednost 2 cm v sprednji formuli je dosežena:

Območje Enegona = 24,72 cm

Reference

1. C. In. Do. (2003). Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Uredniška skupina Patria.
3. Osvobojen, k. (2007). Odkrijte poligone. Benchmark Education Company.
4. Hendrik, v. (2013). Splošni poligoni. Birkhäuser.
5. Iger. (s.F.). Matematika Prvi semester Tacaná. Iger.
6. Jr. Geometrija. (2014). Poligoni. Lulu Press, Inc.
7. Miller, Heeren in Hornsby. (2006). Matematika: sklepanje in aplikacije (deseta izdaja). Pearson Education.
8. Patiño, m. (2006). Matematika 5. Uredništvo Progreso.