Formula enačb druge stopnje, kako jih rešiti, primeri, vaje
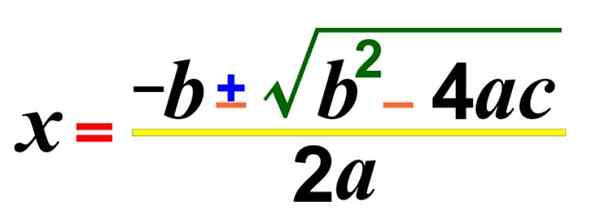
- 3410
- 377
- Miguel Gutmann DVM
The Druga stopnja ali kvadratne enačbe In neznano imajo obrazec sekira2 + bx + c = 0. Kjer bi ≠ 0, ker bi bila 0, bi se enačba spremenila v linearno enačbo, koeficienti A, B in C pa so realne številke.
Neznano, da se določi, je vrednost x. Na primer 3x enačba2 - 5x + 2 = 0 je popolna enačba druge stopnje.
 Slika 1. Formula za reševanje druge stopnje ali kvadratne enačbe neznanega
Slika 1. Formula za reševanje druge stopnje ali kvadratne enačbe neznanega Obstajajo tudi različice, ki so znane kot nepopolne enačbe drugega stopnje, ki nimajo nobenega izraza, razen v sekira2. Tu je nekaj primerov:
x2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, znani arabski matematik antike, je v svojih delih opisal različne vrste enačb prve in druge stopnje, vendar le s pozitivnimi koeficienti. Vendar je bila francoska matematika Odločnost:
To je splošna formula, ki omogoča reševanje kvadratne enačbe, iskanje korenin ali ničle, tudi če rešitve niso resnične. Obstajajo tudi drugi načini, kako jih rešiti.
[TOC]
Kako rešiti enačbe drugega razreda?
Enačbe druge stopnje lahko rešite z zgoraj navedeno formulo, obstajajo tudi drugi algebrski postopki, ki lahko delujejo v nekaterih enačbah.
Predlagano enačbo bomo rešili na začetku s formulo, veljavno metodo za katero koli drugo stopnjo enačbe z neznanimi:
3x2 - 5x + 2 = 0
Za uporabo formule pravilno ugotavljamo, da:
- do Je koeficient izraza z x2
- b Je koeficient linearnega izraza
- c je neodvisni izraz.
Prepoznajmo jih iz iste enačbe:
A = 3
B = -5
C = 2
Upoštevajte, da je treba upoštevati znak, ki spremlja koeficient. Zdaj te vrednosti nadomestimo v formuli:
V števcu je simbol "več - manj" ±, kar pomeni, da je mogoče količino s korenino jemati kot pozitivno in tudi kot negativno. Enačba druge stopnje ima največ dve resnični rešitvi in ta simbol jo upošteva.
Pokličimo x1 in x2 Temu dvema rešitvama, potem:
x1 = (5+1) / 6 = 1
x2 = (5-1)/6 = 4/6 = 2/3
Ločljivost s faktorizacijo
Nekatere enačbe druge stopnje so sestavljene iz trinomij, ki so zlahka faktor. Če je tako, je ta metoda veliko hitrejša. Razmislite o enačbi:
x2 + 7x - 18 = 0
Faktorizacija ima to obliko:
Vam lahko služi: skladnost: skladne številke, merila, primeri, vaje(x +) ⋅ (x -)
Prazni prostori so napolnjeni z dvema številkama, ki se ob pomnitanju v 18, in ko jih odštejemo, 7 jih je 7. Znaki v oklepajih so izbrani s tem kriterijem:
-V prvi oklepaji je postavljen znak med prvim in drugim mandatom.
-In v drugi oklepaji gre za produkt vidnih znakov.
Kar zadeva številke, so v tem primeru enostavno: sta 9 in 2. Najstarejši je vedno postavljen v prvo oklepalo, kot je ta:
x2 + 7x - 18 = (x + 9). (x - 2)
Bralec lahko preveri distribucijsko lastnost, ki pri razvoju izdelka desne strani enakosti dobimo trinomial leve. Zdaj je enačba napisana:
(x + 9) ⋅ (x - 2) = 0
Da se enakost izpolni, je dovolj, da je eden od obeh dejavnikov nič. Torej, v prvem je treba storiti1 = -9 ali je morda, da je drugi faktor preklican, v tem primeru x2 = 2. To so rešitve za enačbe.
Grafična metoda
Korenine ali rešitve enačbe druge stopnje ustrezajo križitvam prispodobe y = = sekira2 + bx + c Z vodoravno osi ali osi x. Tako da bomo z grafikom ustrezne prispodobe našli rešitev enačbe druge stopnje, ki dela y = 0.
Rezi prispodobe z vodoravno osi predstavljajo rešitve enačbe sekira2 + bx + c = 0. Prispodob, ki reže samo vodoravno osi na eni točki, ima en sam koren in to bo vedno točka parabole.
In končno, če prispodoba ne razreže na vodoravno osi, ustrezna enačba sekira2 + bx + c = 0 Manjka resničnih rešitev.
Izdelava ročnega grafa je lahko naporna, vendar je z uporabo programov, ki grafirajo na spletu, zelo preprosta.
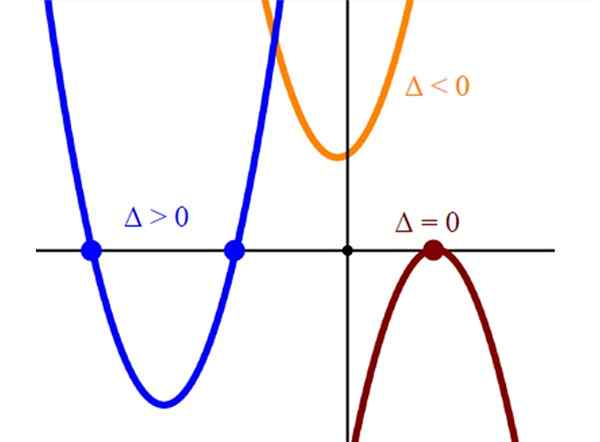 Slika 2. Grafični prikaz treh vrst prispodobe z dvema, eno in brez križišča z vodoravno osi. Vir: Wikimedia Commons.
Slika 2. Grafični prikaz treh vrst prispodobe z dvema, eno in brez križišča z vodoravno osi. Vir: Wikimedia Commons. Ločljivost z znanstvenim kalkulatorjem
Številni modeli znanstvenih kalkulatorjev imajo možnost reševanja enačb druge stopnje (in tudi drugih vrst enačb). Če želite vedeti, morate pregledati meni.
Ko je izbrana možnost kvadratne enačbe neznanega, meni zahteva, da vnese vrednosti koeficientov A, B in C in vrne resnične rešitve, če obstajajo. Obstajajo tudi modeli znanstvenih kalkulatorjev, ki delajo s kompleksnimi številkami in ponujajo te rešitve.
Vam lahko služi: večkratniki 2: kaj so in razlagaDiskriminacija iz enačbe druge stopnje
Če želite vedeti, ali ima enačba resnične rešitve ali ne, in koliko jih je, ne da bi bilo treba najprej rešiti, je diskriminator opredeljen kot znesek pod kvadratnim korenom:
Δ = b2 - 4ac
Glede na diskriminatorni znak je znano, koliko rešitev ima enačba v skladu s tem merilom:
-Dve resnični rešitvi: δ> 0
-Prava rešitev (ali dve enaki rešitvi): Δ = 0
-Brez prave rešitve: δ < 0
Na primer, koliko rešitev ima enačba druge stopnje -7x2 +12x + 64 = 0? Identificiramo koeficiente:
A = -7
B = 12
C = 64
Δ = b2 - 4AC = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
Enačba ima dve rešitvi. Zdaj pa poglejmo to:
x2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
To je enačba z edinstveno ali dvema enakima rešitvama.
Primeri preprostih enačb druge stopnje
Na začetku smo rekli, da bi lahko bile enačbe druge stopnje popolne, če je trinomial, in nepopolno, če manjka linearni izraz ali neodvisni izraz. Zdaj pa poglejmo nekatere posebne vrste:
X enačba obrazca2 + mx + n = 0
V tem primeru A = 1 in formula se zmanjša na:
Za to vrsto enačbe in vedno odvisno od preostalih koeficientov lahko metoda faktorizacije deluje dobro, kot smo videli v prejšnjem razdelku.
Nepopolna enačba oblike sekire2 + C = 0
Rešitev, če obstaja, je oblika:
Obstaja resnična rešitev, kadar ima o c negativen znak, če pa imata dva izraza isti znak, bo rešitev namišljena.
Nepopolna enačba oblike sekire2 + Bx = 0
Ta enačba se hitro reši z uporabo faktorizacije, saj je X skupni dejavnik v obeh pogojih. Ena od rešitev je vedno x = 0, druga pa je taka:
sekira2 + Bx = 0
x (ax + b) = 0
AX + B = 0 → X = -B/A
Poglejmo primer. Rešiti:
x2 - 5x = 0
x (x - 5) = 0
Zato x1 = 0 in x2 = 5
Enačbe z imenovalcem
Obstaja več racionalnih enačb, v katerih je neznano lahko prisotno tako v števcu kot v imenovalcu ali celo le v slednjem, z algebrskimi manipulacijami pa se zmanjšajo na kvadratne enačbe.
Način, kako jih rešiti, je, da obe strani enakosti pomnožite z minimalnim skupnim večkratnikom.c.m imenovalcev in nato preuredite izraze. Na primer:
Vam lahko služi: koliko premerov ima obod?Enačbe višjega reda, ki se spremenijo v kvadratno
Obstajajo enačbe višjega reda, ki jih je mogoče s spremenljivo spremembo rešiti, kot da so kvadratne, na primer to enačbo Bicadrada:
x4 - 10x2 + 9 = 0
Naj x2 = U, potem se enačba spremeni v:
ali2 - 10U + 9 = 0
To enačbo hitro rešimo s faktorizacijo in najdemo dve številki, ki sta se pomnožili v 9 in dodali 10. Te številke so 9 in 1:
(U - 9).(U - 1) = 0
Zato so rešitve te enačbe u1 = 9 in u2 = 1. Zdaj vrnemo spremembo:
x2 = 9 → x1 = 3 in x2 = -3
x2 = 1 → x1 = 1 in x2 = -1
Prvotna enačba je po vrstnem redu 4, zato ima vsaj 4 korenine. Primer je -3, -1, 1 in 3.
Preproste rešene vaje
- Vaja 1
Rešite naslednjo kvadratno enačbo z neznanim v imenovalcu:
Najmanjši običajni večkratnik je x (x+2) in se mora pomnožiti na vse izraze:
Enakovredni izraz ostaja:
5x (x+2) - x = x (x+2)
Razvijamo:
5x2 + 10x - x = x2 + 2x
Vsi izrazi se prenašajo na levo od enakosti, na desno pa levo 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
Upoštevamo, saj gre za nepopolno enačbo:
x (4x - 7) = 0
Ena od rešitev je x = 0, druga pa je:
4x = 7
x = 7/4
- Vaja 2
Poiščite rešitev enačb druge stopnje:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Rešitev
Iz te enačbe poznamo δ determinant, ker je bil izračunan kot primer prej, zato ga bomo izkoristili in izrazili formulo topila na naslednji način:
x1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
x2 = (-12 -44) / -14 = 4
Rešitev b
Kvadratni trinomial x2 - 6x + 9 je fakObiziran, saj je popoln kvadratni trinomial:
x2 - 6x + 9 = (x-3)2 = 0
Rešitev te enačbe je x = 3.
- Vaja 3
Kakšna je enačba, katere rešitve so 3 in 4?
Rešitev
Faktorizirani izraz je:
(x - 3) ⋅ (x - 4) = 0
Uporaba distribucijske lastnosti:
x2 - 4x -3x + 12 = 0
Dva osrednja izraza sta si podobna in ju je mogoče zmanjšati, saj je: odhod:
x2 - 7x + 12 = 0
Reference
- Baldor. 1977. Elementarna algebra. Venezuelske kulturne izdaje.
- Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
- Jiménez, r. 2008. Algebra. Dvorana Prentice.
- Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
- Zapata, f. 4 načini za reševanje enačbe druge stopnje. Okreval od: Francesfizike.Blogspot.com.
- Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.
- « Dodatna struktura polimerov, značilnosti, delovanje, uporabe
- Značilnosti in primeri notranje motivacije »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)