Splošna enačba parabole (primeri in vaje)

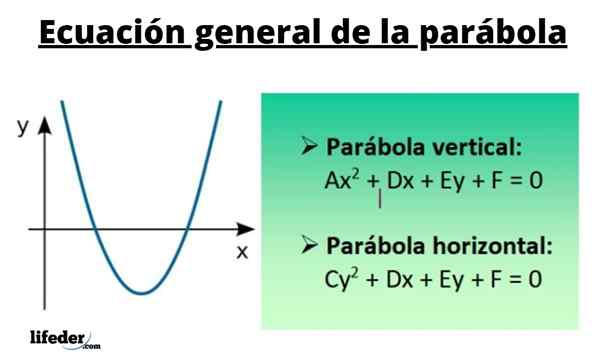
The Prispodoba Splošna enačba vsebuje kvadratne izraze v x in v in, pa tudi linearni izrazi v obeh spremenljivkah in neodvisni izraz. Prva os simetrije je vzporedna z navpično os, drugo pa je vodoravna os.

Na splošno kvadratna enačba, ki nima prekrižanega izraza Xy Napisano je kot:

Sekira² + Cy² +Dx + ey + f = 0

Vrednosti A, C, D, E in F so realne številke. Nalaganje pogojev pri ∙ c = 0 in a+c ≠ 0 je krivulja, ki izhaja iz grafice točk, ki izpolnjujejo to enačbo, parabola.

Primer 1

Za navpično prispodobo je njegova splošna enačba:

Sekira² + Dx + ey + f = 0

Kjer se a in e razlikujeta od 0. Z drugimi besedami, ko se pojavi izraz z x², Prispodoba je navpična.

Primer 2

Za svoje delo imate za vodoravno prispodobo:

Cy² + Dx + ey + f = 0

Tukaj sta C in D tudi različni od 0, zato kvadratni izraz ustreza in².

Vsekakor je splošna enačba prispodobe kvadratna v eni od spremenljivk, v drugem.

Prispodobi

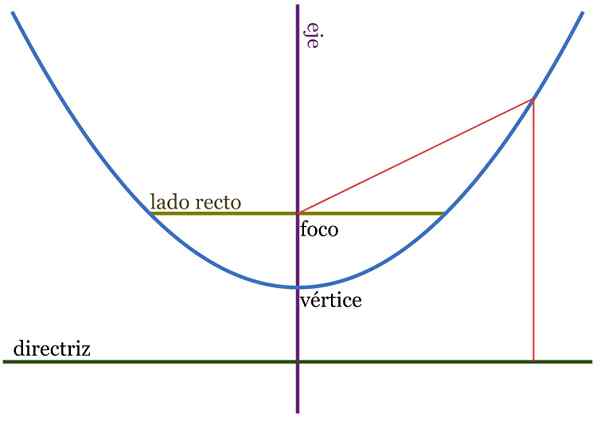Slika 2. Prispodobi. Razdalja QF in QH sta enaki. Vir: Wikimedia Commons.

Parabola, opredeljena kot geometrijsko mesto, je sestavljena iz niza točk ene ravnine, ki se enači z druge točke, imenovane osredotočenost In tudi črte, znane kot naravnost smernica.

Iz splošne enačbe je mogoče preučiti prispodobo tako, da določite njegove elemente. Vključno s fokusom in smernicami, ti elementi, ki so na kratko opisani:

-Os, ki se nanaša na simetrično os parabole, je lahko vodoravna (vzporedno z osjo abscisa) ali navpično (vzporedno z osi ordinatov).

Vam lahko služi: skupni dejavnik za razvrščanje izrazov: primeri, vaje

-Orientacija, kar posledično ustreza orientaciji osi. Prispodoba je navpična, če je njegova simetrična os navpična in je vodoravna, ko je tudi os.

-Vertex, Je točka, v kateri os seka prispodobo.

-Osredotočenost, točka, ki se nahaja na osi, znotraj prispodobe in na daljavo str točke. Vse točke parabole enačasta osredotočenosti in smer smernice.

-Parameter, To je razdalja str Med fokusom in vrhom.

-Naravnost smernica, ki je pravokotno na osi y in tudi razdaljo str točke prispodobe, vendar je ne seka, saj je na zunanji strani.

-Ravna stran, To je vrv, ki prehaja skozi fokus in seka prispodoba v dveh točkah, pravokotno na svojo osjo.

-Ekscentričnost, da je v primeru parabole vedno vredna 1.

-Grafični prikaz.

Informacije za določitev vseh teh elementov so vsebovane v splošni enačbi.

Kanonična oblika

Če želite določiti elemente parabole, je včasih priročno prenesti splošno obliko v kanonično obliko istega z metodo dokončanja kvadratov v kvadratni spremenljivki.

Ta kanonična oblika je:

(X-h)² = 4p (y-k)

Kjer je točka (h, k) vrhova V prispodobe. Lahko postane tudi kanonična oblika splošne enačbe, ki razvije pomemben izdelek in preuredi izraze.

Primeri

Primer 1

Naslednje so enačbe parabole na splošno:

a) 4x² + 5y - 3 = 0

b) 1 - 2y + 3x -in² = 0

V A) so identificirani koeficienti: a = 4, c = 0, d = 0, e = 5, f = -3. Je prispodoba, katere os simetrije je navpična.

Vam lahko služi: sintetična delitev

Splošna enačba ostaja v b):

- in² + 3x - 2y + 1 = 0

In koeficienti so: c = -1, d = 3, e = -2 in f = 1.

Primer 2

Naslednja prispodoba je v kanonični obliki:

(Y-1)² = 6 (x-3)

Če želite najti svojo splošno enačbo, se razvije opazen izdelek in oklepaje se izvaja na desni:

in² -2y + 1 = 6x -18

Zdaj so vsi pogoji na levi predani in so priročno razvrščeni:

in² -2y + 1- 6x +18 = 0 → in² - 6x -2y + 19 = 0

Ker je kvadratni izraz in² Je horizontalna prispodoba. Koeficienti so:

C = 1; D = -6; E = -2, f = 19.

Rešene vaje

Vaja 1

Naslednja prispodoba je podana na splošno:

x² -10x -12y - 11 = 0

Prosimo, da ga napiše v kanonični obliki.

Rešitev

Pojdite v kanonično obliko, doseženo je z dokončanjem kvadratov, v tem primeru v spremenljivki x. Izrazi v x se začnejo v oklepajih:

(x² -10x) -12Y - 11 = 0

To, kar je v oklepajih, morate spremeniti v popoln kvadratni trinomial, ki ga dosežemo z dodajanjem 5², to je treba seveda odšteti, ker je drugače izraz spremenjen. Ostaja takole:

(x² −10x+5²) −12y - 11–5²= 0

Trije izrazi v oklepajih predstavljajo popoln kvadratni trinomial (X-5)². Preveriti ga je mogoče z razvojem tega pomembnega izdelka za potrditev. Zdaj prispodoba ostaja:

(X-5)² -12y -36 = 0

Sledi, da upoštevate izraze zunaj oklepaja:

(X-5)² -12 (y +3) = 0

To se končno spremeni v:

(X-5)² = 12 (y +3)

Primer 2

Poiščite elemente prejšnje prispodobe in zgradite svojo grafiko.

Rešitev

Vertex

Vrh parabole ima koordinate V (5, -3)

Lahko vam služi: hepagonska prizma

Os

Vrstica x = 5.

Parameter

Glede vrednosti parametra str ki se pojavlja v kanonični obliki: (x-h)² = 4p (y-k) primerja obe enačbi:

4p = 12

P = 12/4 = 3

Orientacija

Ta prispodoba je navpična in se odpira. Ker se točka nahaja pri x = 5, y = -3, potem je os simetrije navpična črta x = 5.

Osredotočenost

Poudarek je na vrstici x = 5, zato ima tudi koordinato x = 5 tudi.

Koordinata in Osredotočenost mora biti p enote nad k, to je: p + k = 3 + (-3) = 0, potem je fokus v točki (5.0).

Naravnost smernica

Je pravokotna na os, zato je v obliki y = c, saj je razdalja p od točke daleč, vendar zunaj prispodobe pomeni, da je na razdalji p pod k:

y = k -p = -3-3 = -6

Ravna stran

Ta segment se zmanjšuje na prispodobo, prehaja skozi fokus in je vzporeden s smernico, zato je vsebovan v črti y = 0.

Grafični prikaz

Enostavno ga je mogoče pridobiti iz brezplačne spletne grafične programske opreme, kot je Geogebra. V vhodni škatli je postavljen na naslednji način:

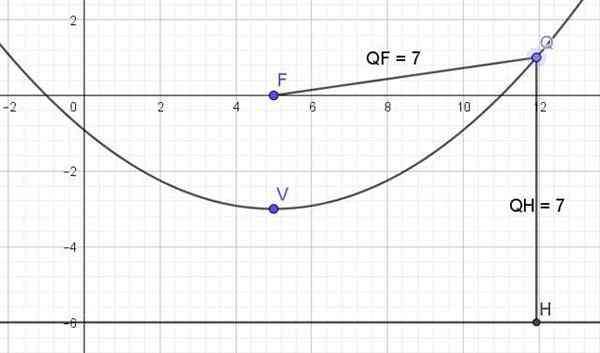Slika 3. Graf prispodobe x² -10x -12y - 11 = 0. Vir: f. Zapata.

Reference

1. Baldor. 1977. Elementarna algebra. Venezuelske kulturne izdaje.
2. Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
3. Jiménez, r. 2008. Algebra. Dvorana Prentice.
4. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.