Enačba kontinuitete

Pojasnjujemo, kakšna je enačba kontinuitete, njena formula, aplikacije, primeri in predlagate vaje za reševanje

Kakšna je enačba kontinuitete?

The Enačba kontinuitete, Za slavo tekočino ugotovi, da skupna masa tekočine, ki kroži skozi cev, brez izgube ali dobička, ostane konstantna. Z drugimi besedami, testo se ohrani brez sprememb, ko se tekočina premika.

Neprimerljiva tekočina je, da med tekom ostaja približno konstantna gostota. Na primer, voda je tekočina, ki se v standardnih tlačnih in temperaturnih pogojih šteje za nestisljivo.

Obstaja matematični način izražanja ohranjanja mase v enačbi kontinuitete, ki jo daje:

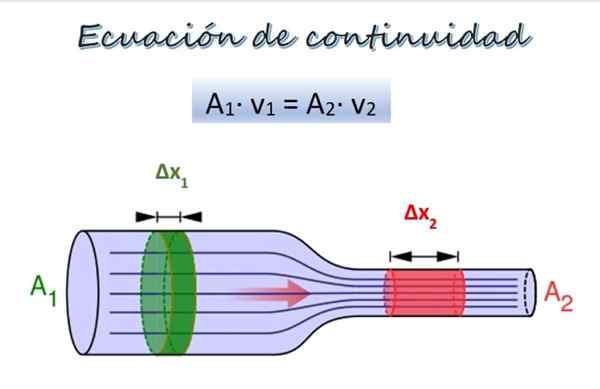
Do₁∙ V₁ = A₂∙ V₂

Kjer v₁ in v₂ Predstavljajo hitrost tekočine v dveh odsekih cevi, medtem ko₁ že₂ So ustrezna območja prereza.

Produc tok In enačba kontinuitete pomeni, da je v celotni cevi pretok konstanten. Tok je znan tudi kot volumen pretoka, Razumemo ga s skrbnim opazovanjem prejšnjega izraza, katerega dimenzije so prostornina na enoto časa.

Formula

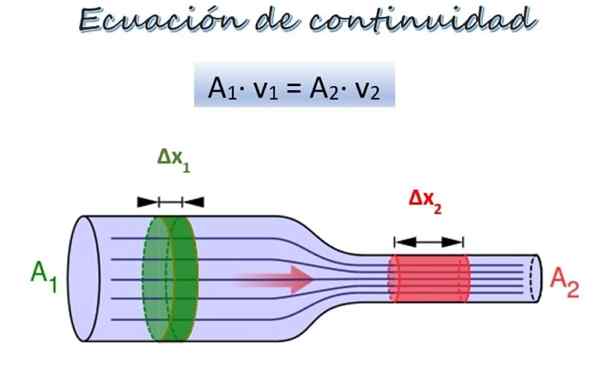Enačba kontinuitete za pretok tekočine vzdolž cevi različnih premerov. Vir: Wikimedia Commons/F. Zapata.

Na zgornji sliki je cev z dvema odsekoma različnih premera in na isti višini, čeprav bi lahko bili na različnih višinah, ne da bi predstavljali težavo.

V oddelku 1 je širše, prerez -sekcijsko območje₁ in tekočina se premika s hitrostjo V₁, Medtem ko je v oddelku 2, ožji, območje prereza₂ in hitrost tekočine je v₂.

Del testa Δm₁ (zelena) se premika po 1. oddelku v času ΔT. V tem obdobju je del ΔM₂ (rdeča) Potovanje skozi 2. poglavje. Ker je tekočina nestisljiva, je njegova gostota v vseh svojih točkah enaka, zato izhaja iz definicije gostote:

Lahko vam služi: konstanta gaze: kaj je, izračun in primeri

Tu je ρ gostota, m je masa in v volumnu. V skladu s tem je masa Δm₁ je enak:

Δm₁ = ρ ∙ V₁

Kjer je zvezek V₁ Je izdelek med presekom in razdaljo Δx₁:

Δm₁ = ρ ∙ (a₁ ∙ Δx₁)

Toda odkar:

Nato del testa Δm₁ Lahko napišete, glede na hitrost in čas ΔT kot:

Δm₁ = ρ ∙ a₁ ∙ Δx₁ = ρ ∙ a₁ ∙ (v₁ ∙ ΔT)

Analogni del Δm je napisan₂ To teče hkrati do oddelka 2:

Δm₂ = ρ ∙ a₂ ∙ Δx₂ = ρ ∙ a₂ ∙ (v₂ ∙ ΔT)

Z ohranjanjem mase:

Δm₁ = Δm₂

In:

ρ ∙ a₁ ∙ V₁ ∙ ΔT = ρ ∙ a₂ ∙ V₂ ∙ ΔT

Ker sta ΔT in ρ preklicana, rezultati:

Do₁ ∙ V₁ = A₂ ∙ V₂

Tok q

Izdelek preseka A s hitrostjo tekočine V imenuje tok in označuje kot Q. Enakovredna je volumnu tekočine na enoto časa skozi cev ali pretok volumna:

 V Volumen in ΔT časovni interval. Pretok v mednarodnem sistemu enot je m³/s, čeprav so kubične noge, galone/min, galoni/s litri/s in galoni/s. Nekateri najbolj uporabljeni faktorji pretvorbe so naslednji:

• 1 m³/S = 264.172 GAL/S
• 1 l/s = 0.001 m³/s
• 1 ft³/S = 0.0283168 m³/s
• 1 l/s = 0,264172 gal/s
• 1 m³/S = 15850.3 gal/min

Upoštevajte, da se s zmanjšanjem preseka cevi hitrost tekočine poveča in obratno, če se presek poveča, se hitrost zmanjša tako, da je pretok konstanten.

Aplikacije in primeri

Enačba kontinuitete se uporablja pri analizi pretoka tekočine v kombinaciji z Bernoullijevo enačbo, pri kateri se upoštevajo razlike hitrosti tekočine v različnih odsekih, pa tudi spremembe tlaka in učinek višine.

Vam lahko služi: neposredni tok

Primer 1

V družinski vrtni cevi, ko voda običajno zapusti curek, ima določen obseg, če pa s prstom postavi na izhod cevi, zmanjša izhodno luknjo, je obseg curka večji.

Tu je enačba kontinuitete izpolnjena, saj se z zmanjšanjem območja izhodne šobe hitrost curka poveča tako, da je površina hitrosti s hitrostjo konstantna.

Primer 2

Vodni curek se zoži, ko pada, saj se njegova hitrost povečuje. Na ta način hitrost izdelka na območje ostane konstantna

Drug primer, kjer je poudarjena enačba kontinuitete, je vodni curek, ki se zoži, ko pade, zaradi povečanja hitrosti vode med padcem.

Na ta način je pretok konstanten, medtem ko curek še naprej teče v laminarnem režimu, to je, da voda nežno pada brez turbulenc ali vrtinčkov.

Rešene vaje

Vaja 1

Voda kroži skozi cev premera 20 cm. Če veste, da je tok 2000 l/s, poiščite hitrost vode v cevi.

• Rešitev

Priročno je izraziti vse v enotah mednarodnega sistema. Najprej se izračuna presek prerez cevi, pri čemer se spomni, da je polmer polovico premera:

A = π ∙ (d/2)²

D = 20 cm = 0.2 m

Zato je območje:

A = π ∙ (d/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

Tok je izražen v m³/s s pomočjo ustreznega pretvorbenega faktorja:

Q = 2000 l/s = 2 m³/s

Iz formule q = a ∙ V hitrost, s katero se tekočina kroži skozi cev, očisti:

Vaja 2

Imate spremenljivo cev prečnega prereza, skozi katero teče voda. V določeni točki je presek 0.070 m² In hitrost vode je 3.50 m/s. Izračunati:

Lahko vam služi: Pascal Princip: Zgodovina, aplikacije, primeri

a) Hitrost vode na drugi točki v cevi, katere območje prereza je 0.105 m².

b) prostornina vode, ki jo v 1 uri izpraznimo z odprtim koncem.

• Rešitev

Uporablja se enačba kontinuitete, ki ustreza toku prve točke s tokom druge. Tok je:

Q = a ∙ V

Za kontinuiteto:

Q₁ = Q₂

Do₁ ∙ V₁ = A₂ ∙ V₂

Zdaj nadomestijo podatke, ki jih posreduje izjava:

• Do₁ = 0.070 m²
• v₁ = 3.50 m/s
• Do₂ = 0.105 m²
• v₂ =?

In razčisti v₂:

Rešitev b

Ker je tok tudi glasnost na enoto časa, mora:

Zato je zvezek V:

V = q ∙ ΔT = (a ∙ v) ΔT

Pretok, ki ga je mogoče izračunati s podatki iz točke 1 ali točko 2, saj je na obeh točkah enak:

Q = a₁ ∙ V₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / s

Če veste, da je 1 ura = 3600 s, je prostornina izpuščene vode:

V = q ∙ ΔT = (0.245 m³ / s) × (3600 s) = 882 m³

V 1 uri se prenašajo 882 m³ vode skozi cev.