Poissonove distribucijske formule, enačbe, model, lastnosti

The Poissonova distribucija Gre.

Poissonovo porazdelitev lahko pogosto uporabimo namesto binomne porazdelitve, dokler so izpolnjeni naslednji opisani pogoji: velik vzorec in majhna verjetnost.

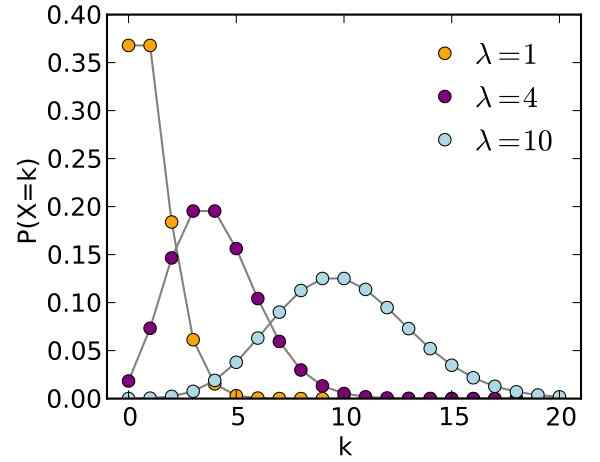
Slika 1. Poissonov graf distribucije za različne parametre. Vir: Wikimedia Commons.

Siméon-Denis Poisson (1781-1840) je ustvaril to distribucijo, ki ima njegovo ime, zelo koristno, ko gre za nepredvidljive dogodke. Poisson je leta 1837 objavil svoje rezultate, raziskovalno delo o verjetnosti pojava napačnih kazenskih kazni.

Kasneje so drugi raziskovalci prilagodili porazdelitev na drugih območjih, na primer število zvezd, ki bi lahko bile v določeni količini prostora, ali verjetnost, da bo vojak umrl zaradi konjskega coza.

[TOC]

Formula in enačbe

Matematična oblika Poissonove distribucije je naslednja:

 - Naključna spremenljivka je in

- μ (včasih tudi označen kot λ) To je povprečni ali distribucijski parameter

- Eulerjeva številka: E = 2.71828

- Verjetnost pridobitve y = k je p

- k To je število uspehov 0, 1,2,3 ..

- n To je število testov ali dogodkov (velikost vzorca)

Diskretne naključne spremenljivke, kot že ime pove, so odvisne od naključja in sprejmejo samo diskretne vrednosti: 0, 1, 2, 3, 4 ..., k.

Povprečje porazdelitve je podano z:

Varianta σ, ki meri disperzijo podatkov, je še en pomemben parameter. Za Poissonovo distribucijo je:

σ = μ

Poisson je ugotovil, da ko se N → ∞ in p → 0 imenuje povprečno μ -tudi pričakovana vrednost- Se nagiba v konstanto:

μ → konstanta

Pomembno: str To je verjetnost pojavljanja dogodka ob upoštevanju celotnega prebivalstva, medtem ko P (y) To je Poissonova napoved glede vzorca.

Model in lastnosti

Poissonova distribucija ima naslednje lastnosti:

-Velikost vzorca je velika: N → ∞.

-Upoštevani dogodki ali dogodki so neodvisni drug od drugega in se pojavljajo naključno.

-Verjetnost Str Kakšen določen dogodek in Pojavi se za določeno časovno obdobje zelo majhno: P → 0.

-Verjetnost več kot enega dogodka v časovnem intervalu je 0.

-Povprečna vrednost je blizu konstanti, ki jo daje: μ = n.P (n je velikost vzorca)

-Ker je disperzija σ enak μ, saj sprejema večje vrednosti, je tudi spremenljivost večja.

-Dogodke je treba enakomerno razporediti v uporabljenem časovnem intervalu.

-Nabor možnih vrednosti dogodkov in To je: 0,1,2,3,4 .. .

Lahko vam služi: Naključni eksperiment: koncept, vzorčni prostor, primeri

-Vsota Yo Spremenljivke, ki sledijo Poissonovi porazdelitvi, so tudi še ena Poissonova spremenljivka. Njegova povprečna vrednost je vsota povprečnih vrednosti teh spremenljivk.

Razlike z binomno porazdelitvijo

Poissonova porazdelitev se razlikuje od binomne porazdelitve v naslednjih pomembnih vidikih:

-Na binomno porazdelitev vpliva tako velikost vzorca S kot tudi verjetnost Str, Toda Poissonova porazdelitev vpliva le v povprečju μ.

-V binomni porazdelitvi možne vrednosti naključne spremenljivke in So 0,1,2,…, namesto pri porazdelitvi Poissona ni zgornje meje za te vrednosti.

Primeri

Poisson je svojo znano distribucijo sprva uporabil v pravnih primerih, na industrijski ravni. V tem procesu se za fermentacijo uporabljajo pridelki kvasovk.

Kvarek je sestavljen iz živih celic, katerih populacija je spremenljiva v času. Pri izdelavi piva je treba dodati potrebno količino, zato je treba vedeti, koliko celic na enoto prostornine.

Med drugo svetovno vojno je bila Poissonova distribucija uporabljena, da bi vedela, ali Nemci resnično kažejo na London iz Calaisa ali preprosto naključno streljajo. To je bilo za zaveznike pomembno, da ugotovijo, kako dobra je tehnologija na voljo nacistom.

Praktične aplikacije

Poissonove distribucijske aplikacije se vedno nanašajo na število časa ali štetje prostora. In ker je verjetnost pojavljanja majhna, je znana tudi kot "zakon redkih dogodkov".

Tu je seznam dogodkov, ki spadajo v eno od teh kategorij:

-Registracija delcev v radioaktivnem razpadu, ki je tako kot rast celic kvasovk, je eksponentna funkcija.

-Število obiskov določene spletne strani.

-Prihod ljudi v vrsto za plačilo ali udeležbo (teorija repov).

-Število avtomobilov, ki gredo skozi določeno točko na cesti, za dani časovni interval.

Slika 2. Količina avtomobilov, ki gredo skozi točko, sledi približno Poissonovi porazdelitvi. Vir: Pixabay.

-Mutacije, ki so jih utrpele v določeni verigi DNK, potem ko so prejele izpostavljenost sevanju.

-Število meteornih premera večje od 1 m padca v letu dni.

-Napake na kvadratni meter tkanine.

-Količina krvnih celic v 1 kubičnem centimetru.

-Klici na minuto na telefonsko izmenjavo.

-Čokoladne iskre, prisotne v 1 kg testa za torto.

-Število dreves, okuženih z napadom na 1 hektar gozda.

Upoštevajte, da te naključne spremenljivke predstavljajo, kolikokrat se dogodek zgodi za določeno obdobje (Klici na minuto na telefonsko izmenjavo) ali določeno območje vesolja (Napake tkanine na kvadratni meter).

Vam lahko služi: proporcionalna variacija

Ti dogodki, kot so že ugotovili, so neodvisni od časa, ki je minil od zadnjega dogodka.

Približevanje binomialni porazdelitvi z porazdelitvijo Poissona

Poissonova distribucija je dober pristop k binomski porazdelitvi, dokler:

-Velikost vzorca je velika: n ≥ 100

-Verjetnost p je Majhen: P ≤ 0,1

- μ biti v vrstnem redu: NP ≤ 10

V takih primerih je Poissonova distribucija odlično orodje, saj lahko binomna distribucija v teh primerih postane zapletena.

Rešene vaje

Vaja 1

Seizmološka študija je ugotovila, da je bilo v zadnjih 100 letih po vsem svetu 93 velikih potresov, vsaj 6.0 na Richter -logaritmični lestvici-. Recimo, da je Poissonova porazdelitev v tem primeru ustrezen model. Najti:

a) Povprečni pojav velikih potresov na leto.

b) da P (y) To je verjetnost, da se zgodi in Potresi za naključno izbrano leto poiščite naslednje verjetnosti:

Str(0), Str(1), Str (2), Str (3), Str (4), Str (5), Str (6) in Str (7).

c) Resnični rezultati študije so naslednji:

- 47 let (0 potresi)

- 31 let (1 potresi)

- 13 let (2 potresi)

- 5 let (3 potresi)

- 2 leti (4 potresi)

-  0 let (5 potresov)

- 1 leta (6 potresov)

- 1 leta (7 potresov)

Kako so ti rezultati pri rezultatih v pododdelku B? Ali je Poissonova distribucija dobra izbira za modeliranje teh dogodkov?

Rešitev)

a) potresi so dogodki, katerih verjetnost str Je majhen in razmišljamo o omejenem obdobju, enem letu. Povprečni potresi so:

μ = 93/00 potresi / leto = 0.93 potresov na leto.

Rešitev B)

b) Za izračun zahtevanih verjetnosti se vrednosti nadomestijo v formuli, podani na začetku:

Na primer najti P (2), Kar bi bila verjetnost, da bosta na leto na voljo dva velika potresa:

y = 2

μ = 0.93

E = 2.71828

In to je verjetnost, da je na leto 7 velikih potresov:

Je precej manj kot p (2).

Rezultati so navedeni spodaj:

P (0) = 0.395, p (1) = 0.367, p (2) = 0.171, p (3) = 0.0529, p (4) = 0.0123, p (5) = 0.00229, P (6) = 0.000355, p (7) = 0.0000471.

Na primer, lahko bi rekli, da obstaja verjetnost 39.5 %, da v določenem letu ne pride do velikega potresa. Ali da je v tem letu 5,29 %, da se v tem letu pojavijo 3 veliki potresi.

Rešitev C)

c) frekvence se analizirajo, pomnožijo z n = 100 let:

39.5; 36.7; 17.1; 5.29; 1.23; 0.229; 0.0355 in 0.00471.

Vam lahko služi: algebrski derivati

Na primer:

- Frekvenca 39.5 označuje, da v 39.Pojavi se 5 od 100 let ali velikih potresov, lahko bi rekli, da je povsem blizu resničnega 47 -letnega rezultata brez velikega potresa.

Primerjajmo še en Poissonov rezultat z resničnimi rezultati:

- Vrednost, pridobljena od 36.7 pomeni, da je v obdobju 37 let 1 velik potres. Pravi rezultat je, da je bil čez 31 let 1 velik potres, kar je dobro naključje z modelom.

- 17 je pričakovati.1 leta z 2 velikimi potresi in znano je, da sta v 13 letih, ki je tesna vrednost, v veljavi 2 veliki potresi.

Zato je Poissonov model sprejemljiv za ta primer.

Vaja 2

Družba ocenjuje, da število komponent, ki pred zaključkom 100 ur delovanja ne uspejo, sledi Poissonovi distribuciji. Če je povprečno število napak takrat 8, poiščite naslednje verjetnosti:

a) da komponenta ne uspe v 25 urah.

b) okvara manj kot dve komponenti, v 50 urah.

c) da vsaj tri komponente ne uspejo v 125 urah.

Rešitev)

a) Znano je, da je povprečna napaka v 100 urah 8, zato se v 25 urah pričakuje četrti del napak. To bo parameter μ.

Zahteva se verjetnost, da ne bo uspela 1 komponenta, naključna spremenljivka je "komponente, ki ne uspejo pred 25 urami" in njegova vrednost je y = 1. Z zamenjavo v verjetnosti funkcije:

 b) Zdaj je naključna spremenljivka "komponente, ki ne uspejo pred 50 urami". Parameter je μ = 4, Ker je pričakovana vrednost napak v 50 urah 4.

Vendar je vprašanje verjetnost, da manj kot dve komponenti ne uspe v 50 urah, ne da ravno 2 komponenta ne uspeta v 50 urah, zato moramo dodati verjetnosti, ki:

-Noben ne uspe

-Ne uspe samo 1

P (manj kot 2 komponenti) = p (0) + p (1)

P (manj kot 2 komponenti) = 0.0183+0.0732 = 0.0915

c) da vsaj 3 komponente ne uspejo v 125, to pomeni, da lahko 3, 4, 5 ali več.

Verjetnost, ki se zgodi vsaj enega od več dogodkov, je enaka 1, razen verjetnosti, da se noben od dogodkov ne bo zgodil.

-Dogodek, ki se zahteva, je, da v 125 urah ne uspeva 3 ali več komponent

-Da se dogodek ne zgodi, pomeni, da manj kot 3 komponente ne uspe, katerih verjetnost je: P (0)+p (1)+p (2)

Parameter μ porazdelitve v tem primeru je:

 μ = 8 + 2 = 10 okvar v 125 urah.

P (padle 3 ali več komponent) = 1- p (0)- p (1)- p (2) =

= 1-0.0026786 = 0.9972

Reference

1. MathWorks. Poissonova distribucija. Okrevano od: je.MathWorks.com
2. Mendenhall, w. 1981. Statistični podatki za upravo in ekonomijo. 3. mesto. izdaja. Uredniška skupina Iberoamerica.
3. Stat Trek. Naučite se statistike. Poissonova distribucija. Obnovljeno od: stattrek.com,
4. Triola, m. 2012. Osnovna statistika. 11. Ed. Pearson Education.
5. Wikipedija. Poissonova distribucija. Pridobljeno iz: v.Wikipedija.org