Matematika

Formule korelacijskega koeficienta, izračun, razlaga, primer

Formule korelacijskega koeficienta, izračun, razlaga, primer

On korelacijski koeficient V statistiki je kazalnik, ki meri trend dveh kvantitativnih spremenljivk x in y, da imata razmerje med linearnostjo ali sorazmernostjo med njimi.

Na splošno sta pari spremenljivk x in y dve značilnosti iste populacije. Na primer, X je lahko višina osebe E in njena teža.

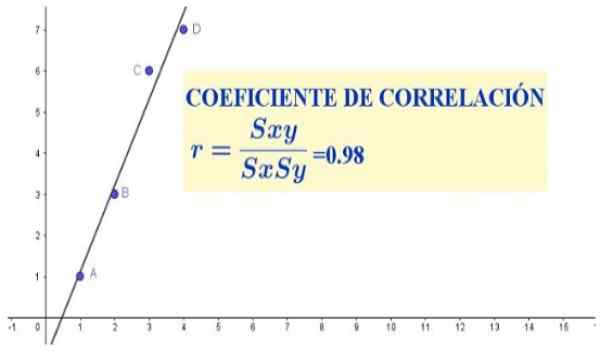
Slika 1. Koeficient korelacije za štiri podatkovne pare (x, y). Vir: f. Zapata.

V tem primeru bi korelacijski koeficient pokazal, ali obstaja razmerje med sorazmernostjo med višino in težo določene populacije.

Pearsonov koeficient linearne korelacije je označen s pismom r male črke in njegove minimalne in največje vrednosti so -1 oziroma +1. 

Vrednost r = +1 bi pomenila, da so celotni pari (x, y) popolnoma poravnani in da ob rasteh X raste v istem deležu. Po drugi strani pa bi bil, če se zgodi, da je r = -1, tudi nabor parov popolnoma poravnan, vendar v tem primeru, ko X raste, in se zmanjšuje v istem deležu.

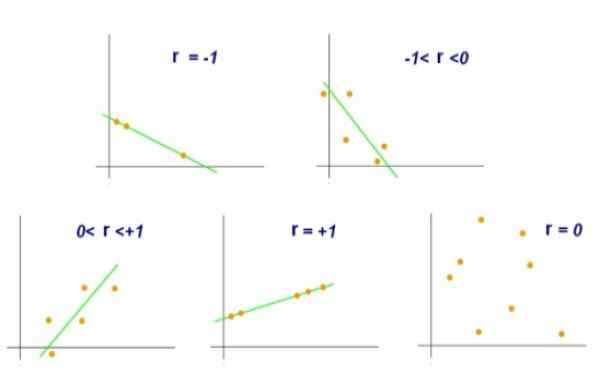Slika 2. Različne vrednosti koeficienta linearne korelacije. Vir: Wikimedia Commons.

Po drugi strani pa vrednost r = 0 kaže, da med spremenljivkami x in y ni linearne korelacije. Medtem ko vrednost r = +0,8 kaže, da se pari (x, y) ponavadi združijo na eno stran in drugo določeno črto.

Formula za izračun korelacijskega koeficienta r ​​je naslednja:

Kjer števec predstavlja kovarianco med spremenljivkami x in y, medtem ko je imenovalec produkt standardnega odstopanja za spremenljivo x in standardni odklon za spremenljivko in.

Kako izračunati korelacijski koeficient?

Koeficient linearne korelacije je statistični znesek, ki je vključen v znanstvene kalkulatorje, v večini preglednic in statističnih programov.

Vam lahko služi: hiperbolični paraboloid: definicija, lastnosti in primeri

Vendar je priročno vedeti, kako se uporablja formula, ki jo določa, in za to se bo prikazal podroben izračun, izveden na majhnem naboru podatkov.

In kot je navedeno v prejšnjem razdelku, je korelacijski koeficient SXY kovariance, deljeno s produktom standardnega odklona SX za spremenljivke X in SY za spremenljivko in.

Kovarijanca in variance

SXY kovariance je:

Sxy = [σ (xi -) (yi -)] / (n -1)

Kjer vsota gre od 1 do n parov (xi, yi). E so aritmetične nogavice podatkov Xi e yi.

Svoj del je standardni odklon za spremenljivo x kvadratni koren variance nabora podatkov XI z I od 1 do N:

Sx = √ [σ (xi -)^2) / (n -1)]

Podobno je standardni odklon za spremenljivko in je kvadratni koren variance nabora podatkov Yi, z I od 1 do N:

Sy = √ [σ (yi -)2 ) / (N-1)]

Ilustrativni primer

Da bi podrobno pokazali način izračuna koeficienta korelacije, bomo vzeli naslednji niz štirih parov podatkov 

(X, y): (1, 1); (23); (3, 6) in (4, 7).

Najprej izračunamo aritmetično srednjo vrednost za x in y, kot sledi:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Nato se izračunajo preostali parametri:

SXY kovariance

Sxy = [(1 - 2.5) (1 - 4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. ... .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Vam lahko služi: pravila izpeljave (s primeri)

.. .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Standardni odklon SX

Sx = √ [(-1.5)2 + (-0.5)2 + (0.5)2 + (1.5)2) / (4-1)] = √ [5/3] = 1.29

Standardni odklon Sy

Sx = √ [(-3.25)2 + (-1.25)2 + (1.75)2 + (2.75)2) / (4-1)] = 

√ [22.75/3] = 2.75

Koeficient ograje r

R = 3.5 / (1.29 * 2.75) = 0.98

Interpretacija

V naboru podatkov prejšnjega primera obstaja močna linearna korelacija med spremenljivkami X in Y, ki se kaže tako v razpršenem grafu (ki ga je mogoče videti na sliki 1) in v koeficientu korelacije, ki je vrgla vrednost precej blizu enota.

Če je korelacijski koeficient bližje 1 ali -1, je bolj smiselna nastavitev podatkov na črto, rezultat linearne regresije.

Linearna regresija

Linearna regresijska črta dobimo iz Metoda najmanjših kvadratov. v katerem se parameter regresijske črte dobiva z minimizacijo vsote kvadrata razlike med vrednostjo in oceno ter Yi podatkov N podatkov.

Po drugi strani pa sta parametra A in B regresijske črte Y = A + BX, pridobljena po metodi minimalnih kvadratov,:

*B = sxy / (sx2) Za pobočje

*A = - b za presečišče regresijske črte z osjo in.

Spomnimo se, da je SXY zgoraj definirana kovarianca in SX2 Je varianta ali kvadrat predhodno definiranega standardnega odklona. E so aritmetično sredstvo podatkov x oziroma.

Primer

Korelacijski koeficient se uporablja za ugotovitev, ali obstaja linearna korelacija tipa med dvema spremenljivkama. Uporabno je, kadar so spremenljivke, ki jih je treba preučiti.

Vam lahko služi: pravilo dopisovanja funkcije

Ilustrativni primer, ki ga imamo spodaj: Merilo stopnje debelosti je indeks telesne mase, ki ga dobimo tako, da težo ene osebe delimo na kilograme med višino istega v kvadratnih enotah na kvadrat.

Zaželeno je vedeti, ali obstaja močna povezava med indeksom telesne mase in koncentracijo holesterola HDL v krvi, merjeno v milimolih na liter. V ta namen je bila narejena študija s 533 ljudmi, povzete v naslednjem grafu, v katerem vsaka točka predstavlja podatke osebe.

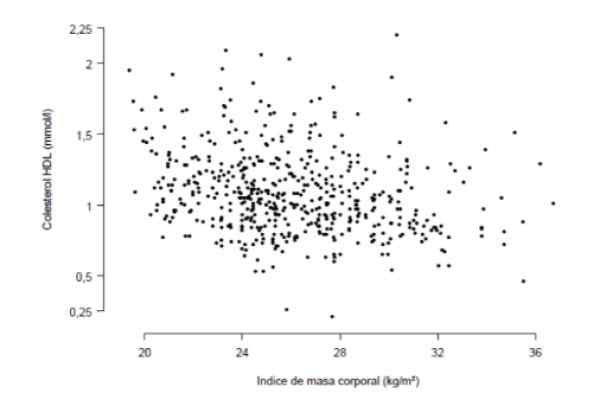Slika 3. Študija IMC in holesterol HDL pri 533 bolnikih. Vir: Aragonski inštitut za zdravstvene vede (IAC).

Iz skrbnega opazovanja grafa izhaja, da obstaja določen linearni (ne zelo izrazit) trend med koncentracijo holesterola HDL in indeksom telesne mase. Kvantitativni ukrep tega trenda je korelacijski koeficient, ki se je za ta primer izkazalo za r = -0,276.

Reference

  1. González c. Splošna statistika. Okreval od: Tarwi.La Molina.Edu.pe
  2. IAC. Aragonski inštitut za zdravstvene vede. Pridobljeno iz: ICS-Aragon.com 
  3. Salazar c. in Castillo s. Načela osnovne statistike. (2018). Pridobljeno iz: dspace.Uce.Edu.Ec
  4. Superprof. Korelacijski koeficient. Okrevano od: Superprof.je
  5. USAC. Priročnik za opisne statistike. (2011). Iztegnjeno od: statistike.inženiring.USAC.Edu.Gt
  6. Wikipedija. Pearsonov korelacijski koeficient. Okrevano od: je.Wikipedija.com.