Koncept euclidijske razdalje, formula, izračun, primer

The Euclidijska razdalja To je pozitivno število, ki kaže na ločitev, ki jo imata dve točki v prostoru, kjer so izpolnjene aksiome in teoreme euklidne geometrije.

Razdalja med dvema točkama A in B evklidskega prostora je dolžina vektorja Ab Pripada edini vrstici, ki gre skozi te točke.

Slika 1 . Enodimenzionalni evklidski prostor, ki ga tvori črta (Ox). Prikazane je več točk na tem prostoru, njihove koordinate in razdalje. (Pripravil Ricardo Pérez).

Prostor, ki ga zaznavamo in kamor premikamo človeška bitja, je tridimenzionalni prostor (3-D), kjer se izpolnjujejo aksiomi in teoremi euklide. V tem prostoru sta dva dimenzionalna podprostora (načrti) in en -dimenzionalni (ravni) (ravni) podprostor.

Euklidski prostori so lahko ena dimenzije (1-D), dvodimenzije (2-D), tri dimenzije (3-D) ali N dimenzije (N-D).

To so točke v enem -dimenzionalnem prostoru X, ki spadajo v orientirano črto (OX), smer od ali do x je pozitiven naslov. Za iskanje točk v tej vrstici se kartezijanski sistem, ki je sestavljen iz dodelitve vsake točke vrstice.

[TOC]

Formula

Euclidijska razdalja D (a, b) je opredeljena med točkami A in B, ki se nahaja na črti, kot je kvadratni koren kvadrata razlik njegovih X koordinat:

D (a, b) = √ ((xb - xa)^2)

Ta opredelitev zagotavlja, da: razdalja med dvema točkama je vedno pozitiven znesek. In da je razdalja med A in B enaka razdalji med B in A.

Slika 1 prikazuje en -dimenzijski evklidski prostor, ki ga tvori črta (volu), in več točk na tej črti. Vsaka točka ima koordinato:

Točka A ima XA koordinata = 2.5, koordinata B xb = 4 in točka c koordinata xc = -2.5

Lahko vam služi: verjetnost frekvence: koncept, kako se izračuna in primeri

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Euclidijska razdalja v dveh dimenzijah

Dva -dimenzionalna evklidna prostor je letalo. Točke evklidske ravnine izpolnjujejo aksiome euklidne geometrije, na primer:

- Na dveh točkah prehaja ena črta. 

- Tri točke na ravnini tvorijo trikotnik, katerega notranji koti vedno dodajo 180 °.

- V trikotniku pravokotnika je kvadrat hipotenuze enak vsoti kvadratov nog.

V dveh dimenzijah ima točka x in y koordinate. 

Na primer, točka P ima koordinate (XP, YP) ​​in točko, ki se je uskladila (XQ, YQ).

Euklidska razdalja med točko P in Q je definirana z naslednjo formulo:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Treba je opozoriti, da je ta formula enakovredna teoremu pitagore, kot je prikazano na sliki 2.

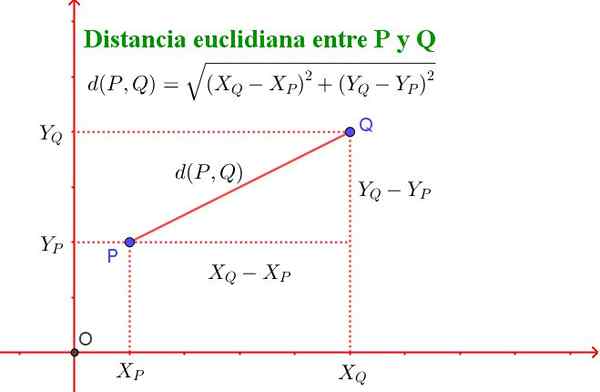Slika 2. Razdalja med dvema točkama P in Q letala se srečuje s teoremom pitagore. (Pripravil Ricardo Pérez).

Neklidijske površine

Niso vsi dve dimenzionalni prostori ne ustrezata evklidski geometriji. Površina krogle je dvodimenzionalni prostor.

Koti trikotnika na sferični površini ne dodajo 180 ° in s tem teorem pitagore ni izpolnjen, zato sferična površina ne izpolnjuje aksiomov evklida.

Euclidijska razdalja v N dimenzijah

Koncept koordinat se lahko razširi na večje dimenzije:

- V 2-D točki P ima koordinate (XP, YP)

- V 3-D točki, ki ima koordinate (XQ, YQ, ZQ)

- V 4-D točki R bo imel koordinate (xr, yr, zr, wr)

- V N-D bo imela točka P koordinate (P1, P2, P3, ..., PN)

Vam lahko služi: graf palic: značilnosti, za kaj je, primeri

Razdalja med dvema P in Q točkami N-dimenzionalnega evklidskega prostora se izračuna z naslednjo formulo:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +… +(qn - pn)^2)

Geometrijsko mesto vseh točk, ki v n-dimenzionalnem evklidskem prostoru, ki so enakovredni iz druge fiksne p točke (središča), tvorijo n-dimenzionalno hipersfera.

Kako izračunati evklidsko razdaljo

Spodaj je razdalja med dvema točkama, ki se nahajata v tridimenzionalnem prostoru Euclidian.

Predpostavimo točko A kartezijanskih koordinat x, y, z, ki jih daje A :( 2, 3, 1) in točka B koordinat B :( -3, 2, 2).

Želite določiti razdaljo med temi točkami, za katere se uporablja splošni odnos:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5.196

Primer

Obstajata dve točki P in Q.  Točka p za kartezijanske koordinate x, y, z, ki jo daje p :( 2, 3, 1) in točka q koordinat q :( -3, 2, 1).

Zahteva se, da najdete koordinate sredine točke M [PQ], ki povezuje obe točki. 

Rešitev:

Domneva se, da ima neznana točka M koordinate (x, y, z).

Ker je m povprečna točka [pq], je treba izpolniti, da je d (p, m) = d (q, m), zato ga je treba izpolniti tudi d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Kot v tem primeru je tretji izraz v obeh članih enak, da je prejšnji izraz poenostavljen na:

Vam lahko služi: absolutna konstanta

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Takrat je enačba z dvema neznankama x in y. Za rešitev problema je potrebna druga enačba.

Točka M pripada črti, ki poteka skozi točke P in Q, ki jih lahko izračunamo na naslednji način:

Najprej je režiserski vektor Pq vrstice: Pq = = .

Nato P.m = Op + do Pq, kje Op Je vektorski položaj točke P in do To je parameter, ki spada v resnične številke. 

Prejšnja enačba je znana kot vektorska enačba črte, ki v kartezijanskih koordinatah sprejema na naslednji način:

= + a =

Enake ustrezne komponente so:

X - 2 = 2 - 5 a; In - 3 = 3 -a; Z - 1 = 0

To pomeni, da je x = 4 - 5a, y = 6 - a, končno z = 1.

Nadomeščen je v kvadratnem izrazu, ki se nanaša x na y:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - A - 2)^2

Poenostavljeno je:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Zdaj se razvija:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

Poenostavljeno je in prekliče podobne izraze pri obeh članih:

4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a

Parameter A:

52 A = 49 + 16 - 4 - 9 = 52, kar je A = 1.

To pomeni, da je x = 4 - 5, y = 6 - 1, končno z = 1.

Na koncu dobimo kartezijanske koordinate sredi točke M segmenta [PQ]:

M: (-1, 5, 1).

Reference

1. Lehmann c. (1972) Analitična geometrija. Uteha.
2. Superprof. Razdalja med dvema točkama. Okrevano od: Superprof.je
3. Ne. Razdalja med povezanimi sublinearnimi sortami. Okreval od: Prometeja.Matem.Ne.mx/
4. Wikipedija. Euclidijska razdalja. Okrevano od: je.Wikipedija.com
5. Wikipedija. Evklidski prostor. Okrevano od: je.Wikipedija.com