Razlike med hitrostjo in hitrostjo (s primeri)

The razlike med hitrostjo in hitrostjo Obstajata, čeprav sta oba povezana s fizičnimi količinami. V skupnem jeziku se en ali drugi izraz uporablja zamenljivo, kot da bi bili sinonim, toda v fiziki jih je treba razlikovati.

V tem članku sta oba koncepta opredeljena, razlike so navedene in pojasnjene s primeri, kako in kdaj velja ena ali druga. Da bi poenostavili, upoštevamo premikajoče se delček in od tam bomo pregledali koncepte hitrosti in hitrosti. 

	Hitrost	Hitrost
Opredelitev	To je prevožena razdalja na enoto časa.	Je premik (ali sprememba položaja) v vsaki enoti časa.
Zapis	v	v
Vrsta matematičnega predmeta	Plezanje.	Vektor.
Formula (za končno časovno obdobje)*	v = ΔS/Δt	v = ΔR/Δt
Formula (za trenutek danega časa) **	v = ds/dt = s '(t)	v = dr/dt = r '(t)
Pojasnilo formule	*Dolžina potovane poti, razdeljena med časovno obdobje, ki se uporablja za potovanje.** V trenutni hitrosti se časovni razpon nagiba v nič. ** Matematična operacija je izpeljanka loka poti kot funkcijo časa glede na čas t časa.	*Vektorski premik, deljen s časom, v katerem je prišlo do premika. ** V trenutni hitrosti se časovno obdobje nagiba na nič. ** Matematična operacija je izpeljanka položaja na čas.
Značilnosti	Za izražanje je potrebno le pozitivno resnično število, ne glede na prostorske dimenzije, v katerih se gibanje pojavi. ** Takojšnja hitrost je absolutna vrednost trenutne hitrosti.	Za izražanje bo morda potrebno več kot eno resnično število (pozitivno ali negativno), odvisno od prostorskih dimenzij, v katerih poteka gibanje. ** Modul trenutne hitrosti je takoj.

Primeri z enakomerno hitrostjo na ravnih odsekih

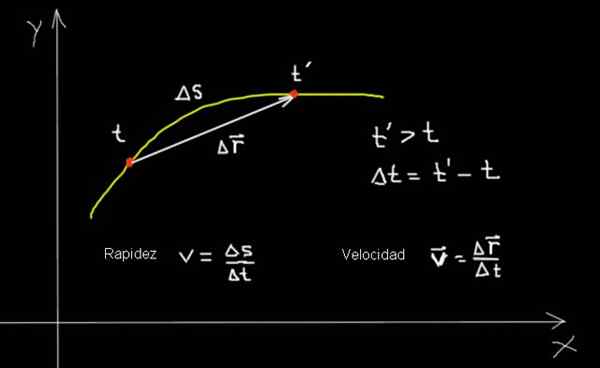
Hitrost in hitrost delca, ki se premika v krivulji. Pripravil: F. Zapata.

V prejšnji tabeli smo povzeli več vidikov hitrosti in hitrosti. In potem se dopolnjuje več primerov, ki ponazarjajo vpletene koncepte in njihove odnose:

Vam lahko služi: paramagnetizem

- Primer 1

Predpostavimo, da se rdeča mrav.

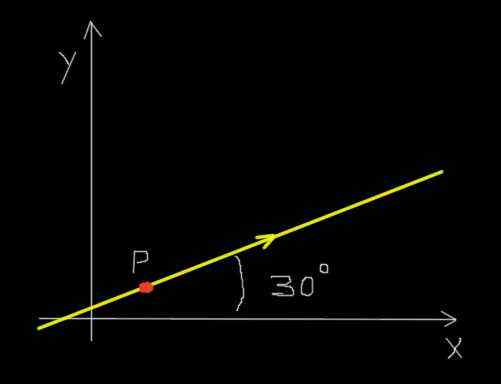Mravlja na pravokotni poti. Vir: f. Zapata.

Poleg tega se mravka premika enakomerno, tako da v časovnem obdobju 0,25 sekunde prečka razdaljo 30 milimetrov. 

Določite hitrost in hitrost mravlja.

Rešitev 

Hitrost mravlje se izračuna z deljenjem razdalje ΔS Toure Tour ΔT.

V = ΔS/ΔT = (30 mm)/(0,25S) = 120 mm/s = 12 cm/s

Stopnja mravlje se izračuna z deljenjem premika Δr med časom, v katerem je bilo omenjeno premik.

Premik je bil 30 mm v smeri 30 ° glede na osi X ali v kompaktni obliki: 

Δr = (30 mm ¦ 30 °)

Opozoriti je mogoče, da je premik sestavljen iz obsega in naslova, saj gre za vektorsko količino. Druga možnost je, da se premik lahko na ta način izraža v skladu s svojimi kartezijanskimi komponentami x in y:

Δr = (30 mm* cos (30 °); 30 mm* brez (30 °)) = (25,98 mm; 15,00 mm)

Stopnja mravlje se izračuna z deljenjem premika med časom, v katerem je bila izvedena:

v = Δr/ΔT = (25,98 mm / 0,25 s; 15,00 mm / 0,25 s) = (103,92; 60,00) mm / s

Ta hitrost v kartezijanskih komponentah x in y y v enotah CM/s je:

v = (10.392; 6.000) cm/s.

Lahko pa se hitrostni vektor izrazi v njegovi polarni obliki (modul ¦ smer), kot je prikazano:

v = (12 cm/s ¦ 30 °).

Opomba: V tem primeru, ker je hitrost konstantna, povprečna hitrost in trenutna hitrost sovpadata. Dokazano je, da je modul trenutne hitrosti takoj hiter.

Vam lahko služi: gostota

Primer 2

Isti mrav iz prejšnjega primera sega od A do B, po B do C in končno od C do A, po trikotni poti, prikazani na naslednji sliki.

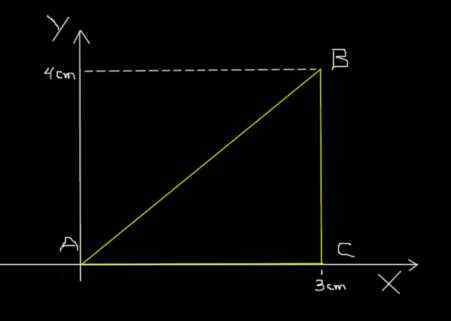Trikotna pot mravlja. Vir: f. Zapata.

Oddelek AB potuje po 0,2s; BC potuje pri 0,1s in končno CA potuje pri 0,3s. Izračunajte povprečno hitrost poti ABCA in povprečno hitrost poti ABCA.

Rešitev 

Za izračun povprečne hitrosti mravlje začnemo z določitvijo skupne prevožene razdalje:

ΔS = 5 cm + 4 cm + 3 cm = 12 cm.

Časovno obdobje, ki se uporablja za celotno pot, je:

ΔT = 0,2s + 0,1s + 0,3S = 0,6 s.

Torej, povprečna hitrost Ant je:

V = ΔS/ΔT = (12 cm)/(0,6s) = 20 cm/s.

Potem se izračuna povprečna hitrost mravljice na poti ABCA. V tem primeru je premik, ki ga je naredil Ant,:

ΔR = (0 cm; 0 cm)

To je zato, ker je premik razlika med končnim položajem manj začetni položaj. Ker sta oba stališča enaka, potem je njihova razlika praznina, kar ima za posledico ničen premik.

Ta ničelni premik je bil izveden v časovnem obdobju 0,6s, tako da je bila povprečna vrsta mravlja:

v =(0 cm; 0 cm)/ 0,6S = (0; 0) cm/ s.

Zaključek: Povprečna hitrost 20 cm/s, Toda povprečna hitrost je na poti ABCA enaka nič.

Primeri z enakomerno hitrostjo na ukrivljenih odsekih

Primer 3

Žuželka se premika na krogu polmera 0,2 m z enakomerno hitrostjo, tako da začenši od A in doseže B, potuje ¼ oboda pri 0,25 s.

Vam lahko služi: hidravlični tisk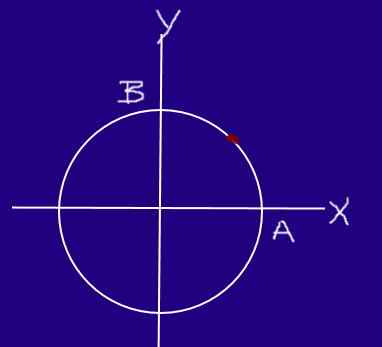Krožni odsek žuželka. Vir: f. Zapata.

Določite hitrost in hitrost žuželke v odseku AB.

Rešitev 

Dolžina oboda med A in B je:

ΔS = 2πr /4 = 2π (0,2m) /4 = 0,32 m.

Uporaba definicije povprečne hitrosti imate:

V = ΔS/ΔT = 0,32 m/0,25 s = 1,28 m/s.

Za izračun povprečne hitrosti je treba izračunati vektor premika med začetnim položajem A in končnim B:

Δr = (0; r)-(r; 0) = (-r; r) = (-0,2; 0,2) m

Uporaba povprečne definicije hitrosti je dosežena:

v = Δr/ ΔT = (-0,2; 0,2) m / 0,25s = (-0.8; 0,8) m/s.

Prejšnji izraz je povprečna hitrost med A in B, izraženim v kartezijanski obliki. Druga možnost je, da se povprečna hitrost lahko izrazi v polarni obliki, to je modul in smer:

| v | = (-0,8)^2 + 0,8^2)^(½) = 1,13 m/s

Naslov = arctan (0,8 / (-0,8)) = Arcan (-1) = -45 ° + 180 ° = 135 ° glede na osi x.

Končno je povprečni hitrostni vektor v polarni obliki: v =(1,13 m/s ¦ 135 °).

Primer 4

Ob predpostavki, da je začetni trenutek žuželke prejšnjega primera 0s od točke A, je vaš vektorski položaj v trenutku, ko je kateri koli t podeljen:

r(t) = [r cos ((π/2) t); R sen ((π/2) t)].

Določite hitrost in takojšnjo hitrost za vsak trenutek t.

Rešitev 

Takojšnja hitrost je izpeljana glede na čas položaja:

v(t) = Dr/dt = [-r (π/2) brez ((π/2) t); R (π/2) cos ((π/2) t)]]

Takojšnja hitrost je modul vektorske takojšnje hitrosti:

v (t) = | v(T) | = π r / 2^½

Reference

1. Alonso m., Finn e. Fizika zvezek I: Mehanika. 1970. Interameriški izobraževalni sklad s.Do.
2. Hewitt, str. Konceptualna fizikalna znanost. Peta izdaja. Pearson.
3. Mladi, Hugh. Univerzitetna fizika s sodobno fiziko. 14. izd. Pearson.
4. Wikipedija. Hitrost. Okrevano od: je.Wikipedija.com
5. Zita, a. Razlika med hitrostjo in hitrostjo. Pridobljeno iz: diferenciator.com