Razlika v formulah, enačbah, primeri, vajah

The Razlika kockov Je binomni algebrski izraz oblike do³ - b³, Kjer sta izraza A in B lahko realna številka ali algebrski izrazi različnih vrst. Primer razlike v kockah je: 8 - x³, Ker je 8 mogoče zapisati kot 2³.

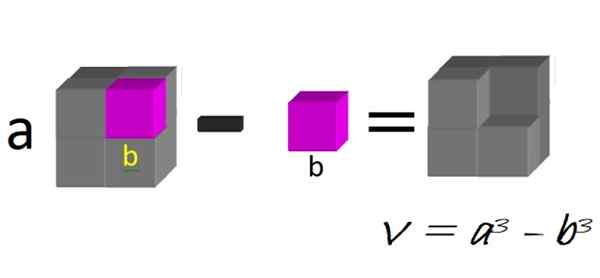
Geometrijsko si lahko omislimo veliko kocko, od strani A, do katere se odšteje majhen bube strani B, kot je prikazano na sliki 1:

Slika 1. Razlika kockov. Vir: f. Zapata.

Obseg nastale slike je natančno razlika v kockah:

V = a³ - b³

Če želite najti alternativni izraz, opazimo, da je mogoče to številko razčleniti na tri prizme, kot je prikazano spodaj:

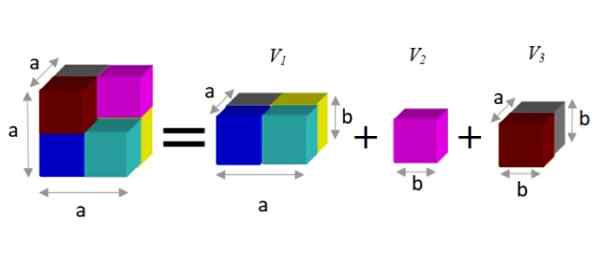Slika 2. Razlika v kockah (levo od enakosti) je enaka vsoti delnih količin (desno). Vir: f. Zapata.

Prizma ima glasnost, ki jo daje produkt svojih treh dimenzij: Širina x visoka globina x. Na ta način je nastala glasnost:

V = a³ - b³ = a².b + b³ + do.b²

Faktor b Skupno je desno. Poleg tega je na zgornji sliki izpolnjena zlasti:

b = (a/2) ⇒ a = b + b

Zato lahko rečemo, da: b = a - b. Tako:

do³ - b³ = B (a² + b² +do.b) = (a-b) (a² + do.b + b²)

Takšen način izražanja razlike v kockah se bo izkazal za zelo koristno v mnogih aplikacijah in bi bil pridobljen na enak način, čeprav je bila manjkajoča stran kocka v kotu drugačna od B = a/2.

Upoštevajte, da je druga oklepalaVeliko je videti na izjemen izdelek kvadrata vsote, vendar prekrižanega izraza ne pomnoži 2. Bralec lahko razvije desno stran, da preveri, ali je učinkovito pridobljen do³ - b³.

[TOC]

Vam lahko služi: kvadratni binomial

Primeri

Obstaja več razlik v kockah:

1 - m⁶

do⁶b³ - 8Z¹²in⁶

(1/125).x⁶ - 27.in⁹

Analizijmo vsakega od njih. V prvem primeru lahko 1 zapišemo kot 1 = 1³ in izraz m⁶ Ostaja: (m²)³. Oba izraza sta popolni kocki, zato je njihova razlika::

1 -M⁶ = 1³ - (m²)³

V drugem primeru so izrazi napisani:

do⁶b³ = (a²B³

8Z¹²in⁶ = 2³ (z⁴)³ (in²)³ = (2z⁴in²)³

Razlika teh kock je: (a²B³ - (2z⁴in²)³.

Končno je frakcija (1/125) (1/5³), x⁶ = (x²)³, 27 = 3³ in in⁹ = (in³)³. Zamenjava vse to v prvotnem izrazu je pridobljena:

(1/125).x⁶  - 27y⁹ = [(1/5) (x²)³ - (3y³)³

Faktorizacija razlike v kockah

Dejstvo Razlika v kockah poenostavlja številne algebrske operacije. Če želite to narediti, je dovolj, da prej uporabite formulo, ki je bila odšteta prej:

Slika 3. Faktorizacija razlike v kockah in izražanju izjemnega količnika. Vir: f. Zapata.

Zdaj je postopek za uporabo te formule sestavljen iz treh korakov:

- Najprej dobimo kubični koren vsakega od pogojev razlike.

- Nato sta zgrajena binomna in trinoma, ki se pojavita na desni strani formule.

- Končno se binomna in trinomialna zamenjava, da dobimo končno faktorizacijo.

Ponazorili bomo uporabo teh korakov z vsakim od primerov razlike zgoraj predlaganih kock in tako pridobili njegovo faktorizirano ekvivalent.

Primer 1

Faktivni izraz 1 -M⁶   Po opisanih korakih. Začnemo s prepisovanjem izraza kot 1 -M⁶ = 1³ - (m²)³ Izvleči ustrezne kubične korenine vsakega izraza:

Potem sta zgrajena binomna in trinomialna:

Lahko vam služi: Teorija čakalnih vrst: Zgodovina, model, kaj je za to in primere za

A = 1

b = m²

Tako:

A - b = 1 - m²

 (do² +do.b + b²) = 1² + 1.m² + (m²)² = 1 + m² + m⁴

 Končno je nadomeščena v formuli A³ - b³ = (a-b) (a² +do.b + b²)::

1 -M⁶ = (1 - m²) (1 + m² + m⁴)

Primer 2

Faktorizirajte:

do⁶b³ -8Z¹²in⁶ = (a²B³ - (2z⁴in²)³

Ker so to popolne kocke, so kubične korenine takoj: a²B in 2Z⁴in², Od tam sledi, da:

- Binomial: a²B - 2Z⁴in²

- Trinomial: (a²B² + do²b. 2Z⁴in² + (do²B +2Z⁴in²)²

 In zdaj je zgrajena želena faktorizacija:

do⁶b³ -8Z¹²in⁶ = (a²B - 2Z⁴in²). [(do²B² + do²b. 2Z⁴in² + (do²B + 2Z⁴in²)²] =

= (a²B - 2Z⁴in²). [do⁴b² + 2. mesto²b.z⁴in² + (do²B + 2Z⁴in²)²]

Načeloma je faktorizacija pripravljena, vendar je pogosto treba poenostaviti vsak izraz. Potem je izjemen izdelek razvit iz vsote - ki se pojavi na koncu in nato doda podobne izraze. Če se spomnimo, da je kvadrat vsote:

(x + y)² = x² + 2xy + in²

Na ta način se razvije pomembna pravica do desnice:

(do²B + 2Z⁴in²)² = a⁴b² + 4²b.z⁴in² + 4z⁸in⁴

 Nadomeščanje razvoja, dobljenega pri faktorizaciji razlike v kockah:

do⁶b³ -8Z¹²in⁶ = (a²B - 2Z⁴in²). [do⁴b² + 2. mesto²b.z⁴in² + do⁴b² + 4²b.z⁴in² + 4z⁸in⁴] =

Nazadnje, združevanje podobnih izrazov in faktor numeričnih koeficientov, ki so vsi pari, dobimo:

(do²B - 2Z⁴in²). [2⁴b² + 6²b.z⁴in² + 4z⁸in⁴] = 2 (a²B - 2Z⁴in²). [do⁴b² + 3. mesto²b.z⁴in² + 2Z⁸in⁴]

Primer 3

Faktorizira (1/125).x⁶  - 27y⁹ Je veliko preprostejši od prejšnjega primera. Najprej so identificirani ustrezniki A in B:

A = (1/5) x²

B = 3y³

Potem jih zamenjajo neposredno na formuli:

(1/125).x⁶  - 27y⁹ = [(1/5) x² - 3y³]. [(1/25) x⁴ + (3/5) x²in³ + 9y⁶]

Vaja rešena

Razlika v kockah je, kot smo rekli, različne aplikacije v algebri. Poglejmo nekaj:

Vam lahko služi: 5 značilnosti kartezijanske ravnine

Vaja 1

Rešite naslednje enačbe:

a) x⁵ - 125 x² = 0

b) 64 - 729 x³ = 0

Rešitev

Najprej je enačba na ta način dejavnik:

x² (x³ - 125) = 0

Ker je 125 popolna kocka, je oklepaja napisana kot razlika v kockah:

x² . (x³ - 5³) = 0

Prva rešitev je x = 0, vendar najdemo več, če naredimo x³ - 5³ = 0, potem:

x³ = 5³ → x = 5

Rešitev b

Leva stran enačbe je napisana kot 64 - 729 x³ = 4³ - (9x)³. Zato:

4³ - (9x)³ = 0

Ker je eksponent enak:

9x = 4 → x = 9/4

Vaja 2

Faktorski izraz:

(x + y)³ - (X - y)³

Rešitev

Ta izraz je razlika v kockah, če v formuli faktorizacije opazimo:

A = x+ in

b = x- y

Potem je binom najprej zgrajen:

a - b = x+ y - (x- y) = 2y

In zdaj trinomial:

do² + do.b + b² = (x+ y)² + (x + y) (x-y) + (x-y)²

Razviti so pomembni izdelki:

(x+ y)² = x² + 2xy +in²

(x+y) (x-y) = x²- in²

(x- y)² = x² - 2xy +in²

Potem morate zamenjati in zmanjšati podobne izraze:

do² + do.b + b² = x² + 2xy +in²+ x²- in²+ x² - 2xy +in² = 3x² + in²

Rezultat faktorizacije:

(x + y)³ - (X - y)³ = 2y. (3x² + in²)

Reference

1. Baldor, a. 1974. Algebra. Venezuelski kulturni uvodnik s.Do.
2. Fundacija CK-12. Vsota in razlika kockov. Okreval od: CK12.org.
3. Akademija Khan. Kocke razlike v faktorizaciji. Okrevano od: je.Khanacademy.org.
4. Matematika je zabavna napredna. Razlika dveh kock. Okrevano od: matematika.com
5. Ne. Faktorizacija razlike v kockah. Pridobljeno iz: DCB.Fi-c.Ne.mx.