Algebrski derivati

Kaj so algebrski derivati?

The Algebrski derivati Sestavljajo preučevanje derivata v posebnem primeru algebrskih funkcij. Izvor pojma iz derivata sega v starodavno Grčijo. Razvoj tega pojma je motivirala potreba po reševanju dveh pomembnih težav, enega v fiziki in enega v matematiki.

V fiziki derivat rešuje problem določanja trenutne hitrosti premikajočega se predmeta. V matematiki omogoča iskanje tangentne črte do krivulje na določeni točki.

Čeprav je res veliko več težav, ki se rešujejo z uporabo izpeljane, pa tudi njene posplošitve, rezultati, ki so pozneje prišli do uvedbe njihovega koncepta.

Pionirji diferencialnega izračuna sta Newton in Leibniz. Preden damo formalno opredelitev, bomo z matematičnega in fizičnega vidika razvili idejo.

Derivat kot do tangentne črte do krivulje

Recimo, da je graf funkcije y = f (x) neprekinjen graf (brez trnih ali tokov ali ločitev) in bodisi a = (a, f (a)) fiksno točko nad njo. Želimo najti enačbo tangentne črte funkciji f v točki A.

Vzemimo še eno točko P = (x, f (x)) grafa, blizu točke A, in izsledimo sušilno črto, ki poteka skozi A in P. Sušilna črta je črta, ki na graf krivulje razreže na eno ali več točk.

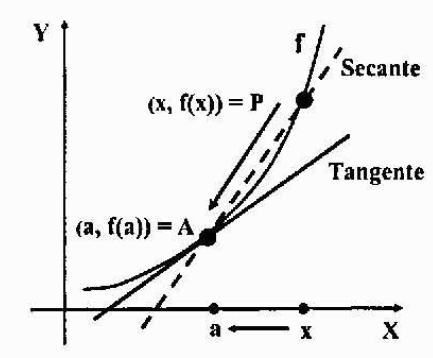
Če želite pridobiti tangentno črto, ki jo želimo, je treba izračunati le, ker že imamo točko vrstice: točka A.

Če premaknemo točko P s grafom in se vedno bolj približamo temu do točke A, se bo prej omenjena suha črta približala tangentni črti, ki jo želite najti. Ob meji, ko se "P nagiba k A", bosta obe vrstici sovpadali, torej tudi na pobočju.

Nagib sekalne linije daje

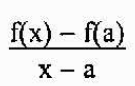
Če rečem, da je P blizu A, je enakovredno reči, da se "x" približa "a". Tako bo naklon tangentne črte na graf F v točki A enak:

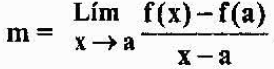
Prejšnji izraz je označen s f '(a) in je opredeljen kot derivat funkcije f v točki "a". Vidimo, da je analitično izpeljanka funkcije na neki točki meja, vendar je geometrijsko naklon črte tangenta do grafikona funkcije v točki.

Vam lahko služi: naključna spremenljivka: koncept, vrste, primeri

Zdaj bomo to pojem videli z vidika fizike. Dosegli bomo enak izraz prejšnje meje, čeprav z drugačno potjo in tako dosegli soglasje definicije.

Derivat kot trenutna hitrost premikajočega se predmeta

Poglejmo kratek primer, kaj pomeni trenutna hitrost. Ko je na primer rečeno, da je avtomobil dosegel cilj s hitrostjo 100 km na uro, to pomeni, da je čez eno uro potoval 100 km.

To ne pomeni nujno, da je bil avto v celotni uri vedno 100 km, vecimeter avtomobila bi lahko v nekaterih trenutkih manj ali več označil. Če je moral stati na semaforju, je bila hitrost v tistem trenutku 0 km. Vendar je bila po eni uri pot 100 km.

To je tisto, kar je znano kot povprečna hitrost in daje količnik prevožene razdalje med pretečenim časom, kot smo ga šele videli. Medtem je trenutna hitrost tista, ki v določenem trenutku (čas) označuje velocimetrsko iglo avtomobila.

Poglejmo to zdaj bolj splošen način. Predpostavimo, da se predmet premika po črti in da je ta premik predstavljen z enačbo s = f (t), kjer spremenljivka T meri čas in spremenljivko S premik, ob upoštevanju njegovega začetka v trenutku t = 0, v tem času je tudi nič, torej f (0) = 0.

Ta funkcija f (t) je znana kot funkcija položaja.

Izraz za takojšnjo hitrost predmeta se išče v fiksnem trenutku. S to hitrostjo ga bomo označili za V (a).

Naj bo vsak trenutek blizu trenutka "a". V časovnem intervalu med "A" in "T" spremembo položaja daje f (t) -f (a).

Povprečna hitrost v tem časovnem intervalu je:

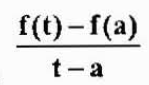
Ki je približek trenutne hitrosti V (a). Ta pristop bo boljši, ko se bo T približal "A". Zato,

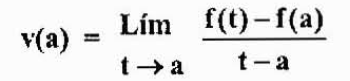
Opazimo, da je ta izraz enak tistemu, pridobljenem v prejšnjem primeru, vendar z drugačne perspektive. To je tisto, kar je znano kot derivat funkcije F v točki "a" in je označeno z F '(a), kot je navedeno zgoraj.

Vam lahko služi: zakoni eksponentov

Upoštevajte, da je sprememba H

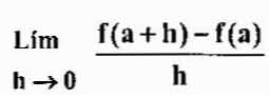
Oba izraza sta enakovredna, včasih pa jih je treba bolj uporabljati za enega namesto drugega, odvisno od primera.

Nato je na splošno opredeljeno, da izhaja iz funkcije f v kateri koli točki "x", ki pripada njegovi domeni kot

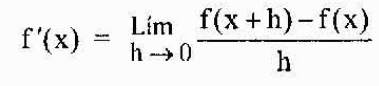
Najbolj običajno zapisovanje, ki predstavlja izpeljavo funkcije y = f (x), je tista, ki smo jo pravkar videli (f 'o y'). Vendar je še ena široko uporabljena zapis zapis Leibniz, ki je predstavljen kot kateri koli od naslednjih izrazov:

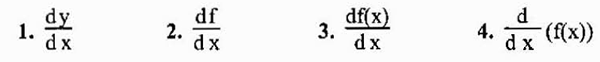
Glede na dejstvo, da je derivat v bistvu omejitev, lahko ali ne obstaja, saj meje ne obstajajo vedno. V primeru, da obstaja, naj bi bila zadevna funkcija na dani točki različna.

Algebrska funkcija

Algebrska funkcija je kombinacija polinomov z vsotami, odštevanjem, izdelki, količniki, moči in radikali.

Polinom je izraz oblike

Str_n= a_nxⁿ+ do_N-1x^N-1+ do_N-2x^N-2+… + A₂x²+ do₁x+a₀

Kjer je n naravno število in vse_Yo, Z i = 0,1,…, n so racionalne številke in_n≠ 0. V tem primeru se reče, da je stopnja tega polinoma n.

Sledijo primeri algebrskih funkcij:

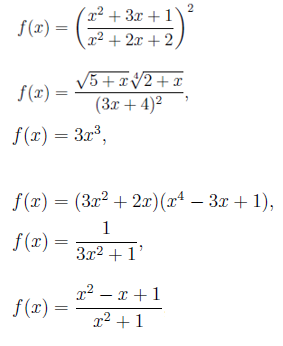
Tukaj eksponentne, logaritmične in trigonometrične funkcije niso vključene. Pravila izpeljave, ki jih bomo videli spodaj, veljajo za funkcije na splošno, vendar jih bomo omejili in uporabili v primeru algebrskih funkcij.

Pravila Derrying

Izhaja iz konstante

Navaja, da je derivat konstante nič. Torej če f (x) = c, potem f '(x) = 0. Na primer, derivat konstantne funkcije 2 je enak 0.

Izhaja iz moči

Če f (x) = xⁿ, potem f '(x) = nx^N-1. Na primer X izpeljan³ Je 3x². Zaradi tega je pridobljeno, da izhaja iz funkcije identitete f (x) = x je f '(x) = 1x^1-1= x⁰= 1.

Drug primer je naslednji: naj bo f (x) = 1/x², potem f (x) = x^-2 in f '(x) = -2x^-2-1= -2x^-3.

Ta lastnost je tudi veljavne korenine, saj so korenine racionalne moči, zgoraj pa je mogoče uporabiti tudi v tem primeru. Na primer, izhaja iz kvadratnega korena

Lahko vam služi: ocena po presledkih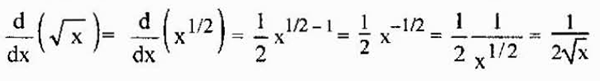

Izhaja iz vsote in odštevanja

Če sta F in G različna funkcija v X, potem je tudi vsota F+g in izpolnjena je, da (f+g) '(x) = f' (x)+g '(x) (x) (x).

Podobno morate (f -g) '(x) = f' (x) -g '(x). Z drugimi besedami, derivat vsote (odštevanje) je vsota (ali odštevanje) derivatov.

Primer

Če je h (x) = x²+X-1, potem

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Izdelek, pridobljen iz izdelka

Če sta F in G različna funkcija v X, je izdelek FG različen tudi v X in je izpolnjeno

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

Posledično ima, če je C konstanta in F je v X različna funkcija, potem je CF tudi v x y (cf) '(x) = cf' (x) različna.

Primer

Če je f (x) = 3x (x²+1) potem

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Izhaja iz količnika

Če sta F in G različna v x in g (x) ≠ 0, potem je f/g tudi v x, ki jih je mogoče razlikovati, in to je izpolnjeno

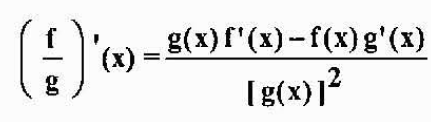
Primer: Če je h (x) = x³/(x²-5x), potem

H '(x) = [(x³) '(X⁵-5x)-(x³) (x⁵-5x) ']/ (x⁵-5x)²= [(3x²) (x⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Pravilo verige

To pravilo omogoča izpeljavo sestave funkcij. Vzpostavlja naslednje: Če je y = f (u) v U različen, in u = g (x) je v x, potem je sestavljena funkcija f (g (x)) v x in je izpolnjena [F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F G (X))] '= f' (g (x)) g '(x).

To pomeni, da je derivat sestavljene funkcije produkt derivata zunanje funkcije (zunanji derivat) z izpeljano notranjo funkcijo (notranji derivat).

Primer

Če f (x) = (x⁴-2x)³, tako

f '(x) = 3 (x⁴-2x)²(x⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Obstajajo tudi rezultati za izračun obratnega derivata funkcije in posploševanje derivatov višjega reda. Prijave so obsežne. Med njimi so izpostavljeni njihov dobiček v optimizaciji in minimalni funkciji.

Reference

1. Alarcon, s., González, m., & Quintana, h. (2008). Različen računanje. Itm.
2. Cabrera, v. M. (1997). 4000 Izračun. Uredništvo Progreso.
3. Castaño, h. F. (2005). Matematika pred izračunom. Univerza v Medellinu.
4. Eduardo, n. Do. (2003). Uvod v izračun. Umbral Edition.
5. Viri, a. (2016). Osnovna matematika. Uvod v izračun. Lulu.com.
6. Purcell, e. J., Rigdon, s. In., & Varberg, D. In. (2007). Izračun. Pearson Education.
7. Saenz, j. (2005). Različen računanje (Drugi izd.). Barquisimeto: hipotenusa.
8. Thomas, g. B., & Weir, m. D. (2006). Izračun: več spremenljivk. Pearson Education.