Kateri so deli kartezijanske ravnine?

The deli kartezijanske ravnine Sestavljen sta iz dveh resničnih, pravokotnih linij, ki kartezijansko ravnino razdelijo na štiri regije. Vsaka od teh regij se imenuje kvadranta in elementi kartezijanske ravnine se imenujejo točke. Letala se skupaj s koordinatnimi osi imenuje Kartezijansko letalo V čast francoskega filozofa Renéja Descartesa, ki je izumil analitično geometrijo.

Dve črti (ali koordinatne osi) sta pravokotni, ker tvorijo kot 90 ° med njima in prečkata v skupno točko (izvor). Ena od črt je vodoravna, ki se imenuje izvor X (ali ABCISA), druga črta.

Pozitivna polovica osi x je desno od izvora in pozitivna polovica osi y je izvora. To omogoča razlikovanje štirih kvadrantov kartezijanske ravnine, kar je zelo koristno pri grafikonu v ravnini.

Kartezijanske ravninske točke

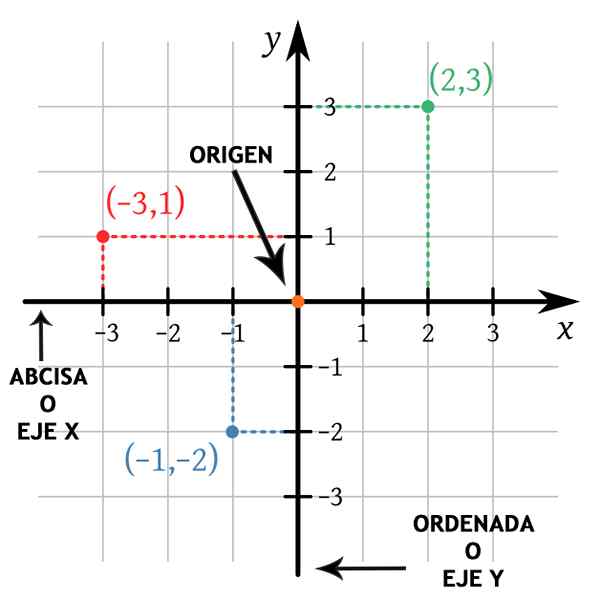
Na vsaki točki Str Letalo lahko dodelite nekaj resničnih številk, ki so njegove kartezijanske koordinate.

Če gredo vodoravna črta in navpična črta Str, In sekate na osi x in osi y do in b nato koordinate Str so (do,b). Poklicano je (do,b) Naroden par in vrstni red, v katerem so napisane številke.

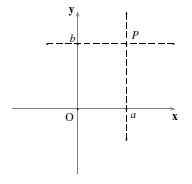
Prva številka, do, To je koordinata v "x" (ali abscisa) in drugem številu, b, To je koordinata v "y" (ali naročen). Zapis se uporablja Str = (do,b).

Očitno je, kako je bila zgrajena kartezijanska ravnina, da izvor ustreza osi "x" in 0 v osi "y", torej, Tudi= (0,0).

Kuadi kartezijanske ravnine

Kot je razvidno iz prejšnjih slik, koordinatne osi ustvarjajo štiri različne regije, ki so kvadranti kartezijske ravnine, ki jih označujemo s črkami in, Ii, iii in Iv In se med seboj razlikujejo v znamenju, da imajo točke, ki so v vsakem od njih.

Kvadrant Yo

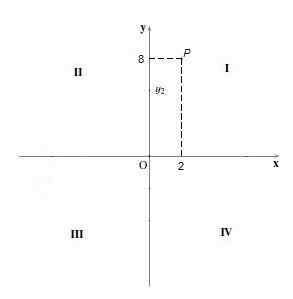
Točke kvadranta Yo To so tisti, ki imata obe koordinati s pozitivnim znakom, to je njihovo X koordinato in njihovo koordinato in so pozitivne.

Na primer točka P = (2.8). Da bi ga graficirali, se točka 2 nahaja na osi "x" in točki 8 na osi "y", nato pa so narisane navpične in vodoravne črte in tam, kjer sekajo Str.

Kvadrant Ii

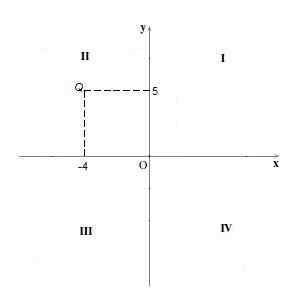
Točke kvadranta Ii Imajo svojo negativno "x" koordinato in pozitivno "y" koordinat. Na primer točka Q = (-4,5). Gre za grafični postopek kot v prejšnjem primeru.

Kvadrant Iii

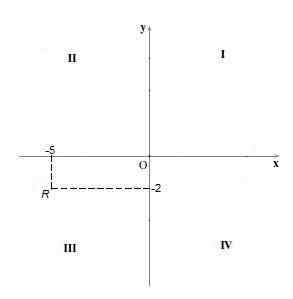
V tem kvadrantu je znak obeh koordinat negativen, torej koordinata "x" in koordinata "y" imata negativna. Na primer točka r = (-5, -2).

Kvadrant Iv

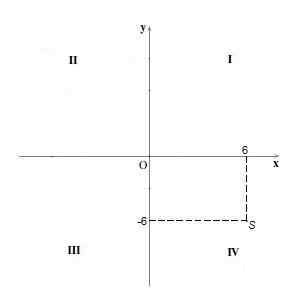
V kvadrantu Iv Točke imajo negativno koordinato "Y" pozitivno in koordinacijo. Na primer točka S = (6, -6).

Reference

1. Fleming, w., & Varberg, D. (1991). Algebra in trigonometrija z analitično geometrijo. Pearson Education.
2. Larson, r. (2010). Prealculus (8 izd.). Cengage učenje.
3. Zvest, J. M., & Viloria, n. G. (2005). Ravna analitična geometrija. Mérida - Venezuela: Venezuelska uredništvo c. Do.
4. Oteyza, e. (2005). Analitična geometrija (Drugi izd.). (G. T. Mendoza, ed.) Pearson Education.
5. Oteyza, e. d., Osnaya, e. L., Garciadiego, c. H., Hoyo, a. M., & Flores, do. R. (2001). Analitična geometrija in trigonometrija (Prvi izd.). Pearson Education.
6. Purcell, e. J., Varberg, d., & Rigdon, s. In. (2007). Izračun (Deveta ed.). Dvorana Prentice.
7. Scott, c. Do. (2009). Geometrija kartezijanske ravnine, del: Analitični koniki (1907) (Ponatis ed.). Vir strele.