Dolžina, teorem in vaje vrvi (geometrija)

A vrv, V ravni geometriji je linijski segment, ki se pridruži dve točki iz krivulje. Govori se, da je črta, ki vsebuje ta segment, sušenje do krivulje. Pogosto je obod, zagotovo pa lahko narišete strune v številne druge krivulje, kot so elipse in prispodobe.

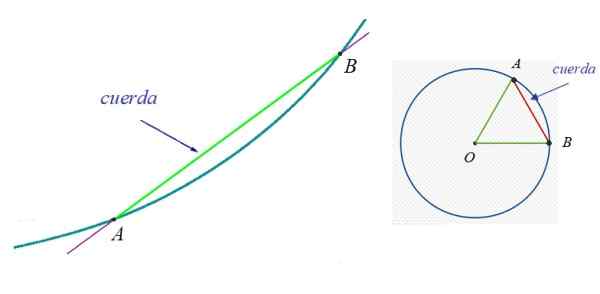
Na sliki 1 na levi je krivulja, ki ji pripadata točke A in B. Vrv med A in B je zeleni segment. Na desni je obod in ena od njihovih strun, saj je mogoče izslediti neskončno.

Slika 1. Na levi vrvi poljubne krivulje in na desni vrvi kroga. Vir: Wikimedia Commons.

V obodu je njegov premer še posebej zanimiv, kar je znano tudi kot Glavna vrv. To je vrv, ki vedno vsebuje središče oboda in dvakrat meri polmer.

Naslednja številka predstavlja polmer, premer, vrv in tudi lok kroga. Pravilno prepoznati vsakega je pomembna pri reševanju težav.

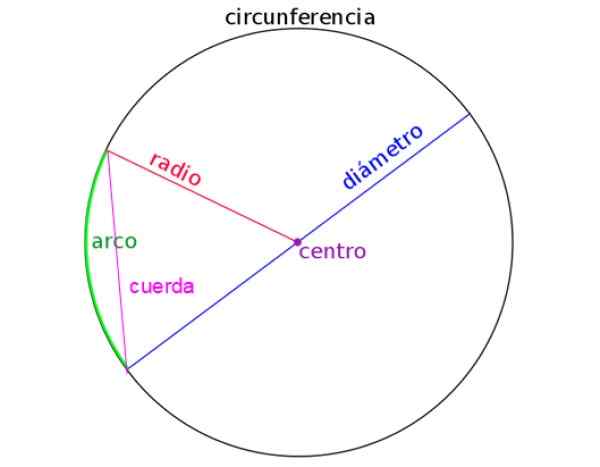Slika 2. Elementi oboda. Vir: Wikimedia Commons.

[TOC]

Dolžina vrvi oboda

Dolžina vrvi lahko izračunamo v krogu, ki se začne s sliki 3a in 3b. Upoštevajte, da je trikotnik vedno oblikovan z dvema enakima stranicama (izosceles): segmente OA in OB, ki merijo R, polmer oboda. Tretja stran trikotnika je segment AB, imenovan C, kar je natančno dolžina vrvi.

Potrebno je narisati črto, pravokotno na vrv C, da se preliva pod kotom θ, ki obstaja med obema radio in katerih točka je središče ali obod. To je osrednji kot -Ker je njegova vrhova središče in bisektorska linija je tudi secat do oboda.

Lahko vam služi: radikalne lastnosti

Takoj nastaneta dva pravokotnika, katerih hipotenuza sta. Ker se bisektor in z njim premer razdeli na dva dela, enaka vrvi, se izkaže, da je ena od nog polovica C, kot je prikazano na sliki 3B.

Iz definicije prsi kota:

sin (θ/2) = nasproti/hipotenusa cateto = (c/2)/r

Zato:

sin (θ/2) = c/2r

C = 2r sen (θ/2)

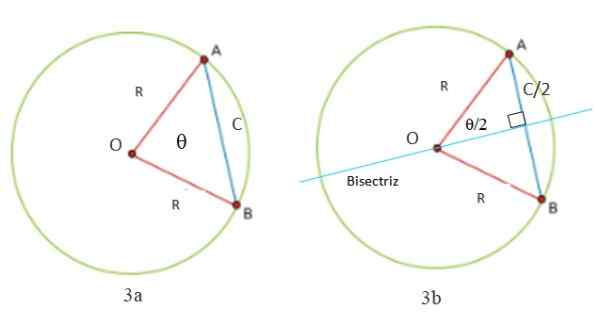Slika 3. Trikotnik, ki ga tvorita dva radija in obodna vrv, je izoscele (slika 3), saj ima dve strani enake. Bisektor ga deli na dva pravokotnika trikotnika (slika 3b). Vir: Pripravil F. Zapata.

String teorem 

Teorem String pravi:

Če se v eni točki sekata dva vrvi, je produkt dolžine segmentov, ki se pojavljajo na enem od strun, enak produktu dolžin segmentov, ki so definirani v drugi vrvi.

Naslednja slika prikazujeta dva niza istega oboda: AB in CD, ki se sekata v točki P. V vrvi AB sta segmenti AP in PB opredeljeni, medtem ko sta CP in PD opredeljena v vrvi CD. Potem v skladu s teoremom:

Ap . Pb = cp . P.S

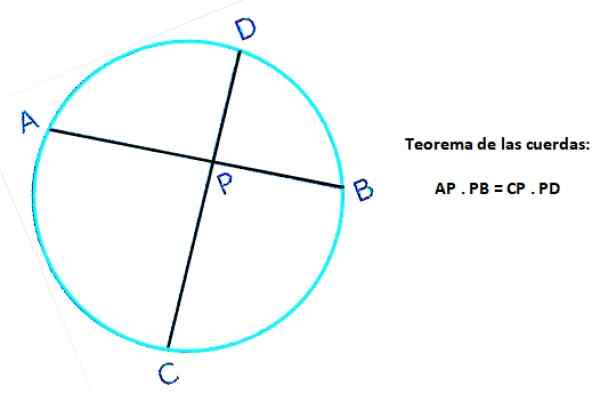Slika 4. Teorem vrvi oboda. Vir: f. Zapata.

Rešene vaje za strune

- Vaja 1

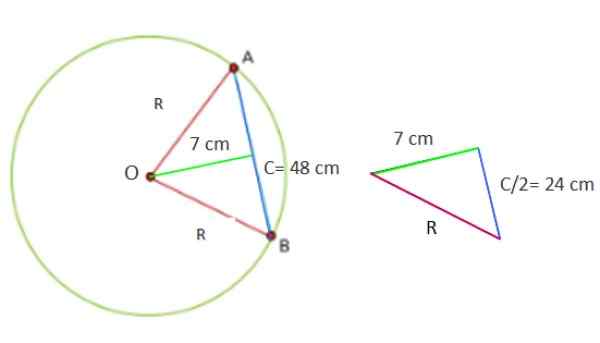
Krog ima 48 cm vrv, ki je od središča 7 cm. Izračunajte območje kroga in obod oboda.

Rešitev  

Za izračun kroga območja je dovolj, da poznamo polmer oboda do kvadrata, saj je izpolnjen:

A = π.R²

Zdaj je številka, oblikovana s predloženimi podatki, pravokotni trikotnik, katerega noge so 7 oziroma 24 cm.

Slika 5. Geometrija za rešeno vajo 1. Vir: f. Zapata.

Zato najti vrednost r² Teorem pitagore C se uporablja neposredno² = a² + b², Ker je R hipotenuza trikotnika:

Vam lahko služi: NULL kot: definicija in značilnosti, primeri, vaje

R² = (7 cm)² + (24 cm)² = 625 cm²

Potem je zahtevano območje:

A = π. 625 cm² = 1963.5 cm²

Kar zadeva obod ali dolžino L oboda, se izračuna z:

L = 2π. R

Zamenjava vrednosti:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Vaja 2

Določite dolžino vrvi kroga, katere enačba je:

x² + in² - 6x - 14y -111 = 0

Znano je, da so koordinate sredine vrvi P (17/2; 7/2).

Rešitev

Srednja točka p vrvi ne pripada obodu, ampak skrajne točke vrvi. Težavo je mogoče rešiti s predhodno navedenim teoremom nizov, najprej pa je priročno.

1. korak: Pridobite kanonsko enačbo oboda

Kanonična enačba oboda s središčem (H, K) je:

(X-h)² + (Y-k)² = R²

Če ga želite pridobiti, je treba dokončati kvadratke:

(x² - 6x) + (in² - 14y) -111 = 0

Upoštevajte, da je 6x = 2.(3x) in 14y = 2.(7y), tako da je prejšnji izraz napisan tako nespremenjen:

(x² - 6x+3²-3²) + (in² - 14y+7²-7²) -111 = 0

In zdaj se spomnite definicije pomembnega izdelka (A-B)² = a² - 2ab + b² Lahko je napisano:

(X - 3)² - 3² + (in - 7)² - 7² - 111 = 0

= (x - 3)² + (in - 7)² = 111 + 3² + 7² → (x - 3)² + (in - 7)² = 169

Obseg ima center (3,7) in radio r = √169 = 13. Naslednja slika prikazuje graf oboda in nizov, ki bodo uporabljeni v teoremu:

Vam lahko služi: kakšnih je 7 elementov oboda?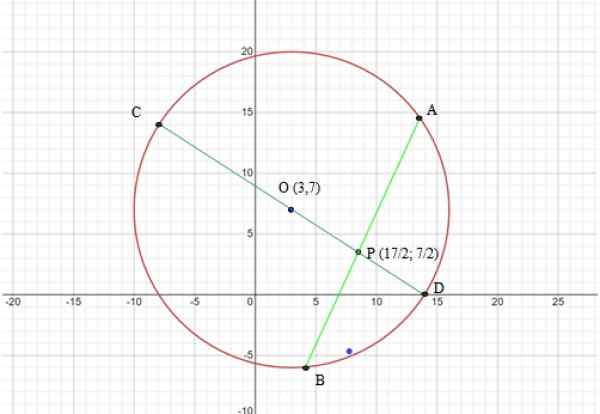Slika 6. Graf oboda vaje Rešena 2. Vir: f. Zapata prek spletnega grafičnega kalkulatorja Mathway.

2. korak: Določite segmente, ki jih je treba uporabiti v teoremu o nizu

Segmenti, ki jih je treba uporabiti, sta CD in AB niza, v skladu s sliko 6 sta oba razrezana v točki P, zato:

Cp . Pd = ap. Pb

Zdaj bomo našli razdaljo med točkami O in P, saj nam bo to dalo dolžino segmenta OP. Če v to dolžino dodamo polmer, bomo imeli segment CP.

Razdalja d_Op Med dvema koordinatnima točkama (x₁,in₁) in (x₂,in₂) je:

d_Op² = OP² = (x₂ - x₁)² + (in₂ - in₁)² = (3- 17/2)² + (7-7/2)² = 121/4 + 49/4 = 170/4

d_Op = OP = √170 /2

Z vsemi dobljenimi rezultati in grafom sestavimo naslednji seznam segmentov (glej sliko 6):

Co = 13 cm = r

OP = √170 /2 cm

Cp = op + r = 13 + √170 /2 cm

PD = OD - OP = 13 - √170 /2 cm

Ap = pb

2.AP = dolžina vrvi

Zamenjava v teoremu z vrvicami:

Cp . Pd = ap . Pb = [(13 +√170 /2) . (13 -√170 /2)] = AP²

[169-170/4] = AP²

253/2 = AP²

AP = √ (253/2)

Dolžina vrvi je 2.AP = 2 (√253/2) = √506

Bi lahko bralec težavo rešil na drug način?

Reference

1. Baldor, a. 2004. Ravna in vesoljska geometrija s trigonometrijo. Kulturne publikacije s.Do. od c.V. Mehika.
2. C-K12. Lenght akorda. Okreval od: CK12.org.
3. Escobar, j. Obod. Okrevano od: matematika.ti.Edu.co.
4. Villena, m. Stožčasto. Pridobljeno iz: dspace.Espol.Edu.Ec.
5. Wikipedija. Vrv (geometrija). Okrevano od: je.Wikipedija.org.