Opredelitev in značilnosti ničnega kota, primeri, vaje

On ničelni kot To je tisti, katerega ukrep je vreden 0, tako v stopinjah kot v radijskem ali drugem sistemu merjenja. Zato nima amplitude ali odpiranja, na primer tiste med dvema vzporednima črtama.

Čeprav se njegova definicija zveni precej preprosta, je ničelni kot zelo uporaben v številnih fizikalnih in inženirskih aplikacijah, pa tudi pri navigaciji in oblikovanju.

Slika 1. Med hitrostjo in pospeševanjem avtomobila je ničelni kot, zato avtomobil gre hitrejši in hitreje. Vir: Wikimedia Commons.

Obstajajo fizične količine, ki jih je treba vzporedno uskladiti, da dosežemo določene učinke: če se avtomobil premakne naravnost na avtocesto in med svojim hitrostnim vektorjem v in njegov vektorski pospešek do Obstaja 0 °, avto se povečuje.

Na naslednji sliki se prikazujejo različne vrste kota, vključno z ničelnim kotom na desno. Kot je razvidno, kot 0 primanjkuje amplitude ali odprtine.

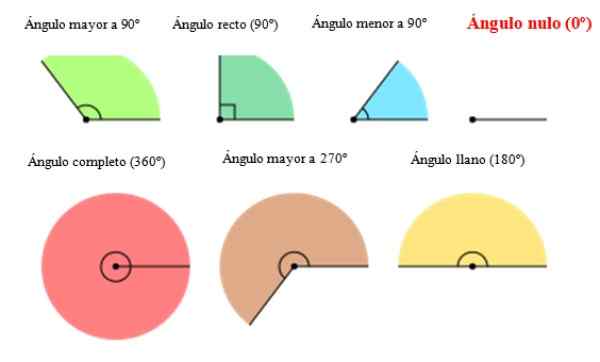Slika 2. Vrste kota, vključno z ničelnim kotom. Vir: Wikimedia Commons. ORIAS [CC BY-SA (https: // CreativeCommons.Org/licence/by-sa/3.0)].[TOC]

Primeri ničelnih kotov

Znano je, da vzporedne črte tvorijo kot nihanje. Ko imate vodoravno črto, je to vzporedno z x -osi kartezijanskega koordinatnega sistema, zato je njen nagib glede nanj 0. Z drugimi besedami, vodoravne črte imajo nič naklona.

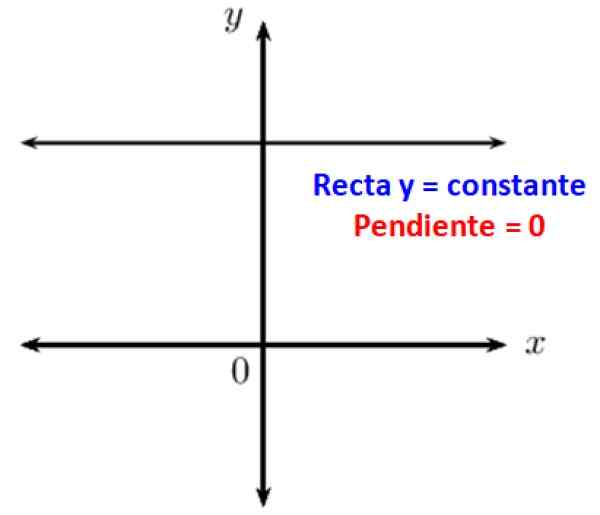Slika 3. Vodoravne črte so v teku nič. Vir: f. Zapata.

Tudi trigonometrični razlogi ničelnega kota so 0, 1 ali neskončnost. Zato je ničelni kot prisoten v mnogih fizičnih situacijah, ki vključujejo operacije z vektorji. Ti razlogi so:

Vam lahko služi: urejen par

-Sen 0º = 0

-cos 0º = 1

-Tg 0 ° = 0

-Sec 0º = 1

-Škoda 0º → ∞

-CTG 0º → ∞

In koristni bodo za analizo nekaterih primerov situacij, v katerih ima prisotnost ničelnega kota temeljno vlogo:

- Učinki ničelnega kota na fizične velikosti

Vsota vektorjev

Ko sta dva vektorja vzporedna, je kot med njima ničen, kot je prikazano na sliki 4 zgoraj. V tem primeru se vsota obeh izvede tako, da postavimo drug za drugim, velikost vektorske vsote.

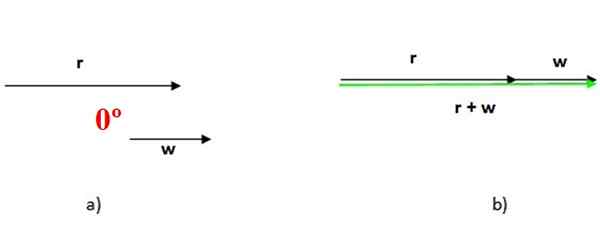Slika 4. Vsota vzporednih vektorjev, v tem primeru je kot med njimi ničelni kot. Vir: f. Zapata.

Ko sta dva vektorja vzporedna, je kot med njima ničen, kot je prikazano na sliki 4 zgoraj. V tem primeru se vsota obeh izvede tako, da postavimo drug za drugim, velikost vektorske vsote

Navor ali navor

Navor ali navor povzroči vrtenje telesa. Odvisno je od obsega uporabljene sile in kako se uporablja. Zelo reprezentativni primer je angleški ključ slike.

Da bi dosegli najboljši učinek obračanja, sila pravokotno velja za ključni ročaj, bodisi navzgor ali navzdol, vendar vrtenja ne pričakujemo, če je sila vzporedna z ročajem.

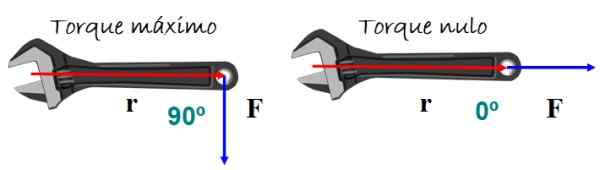Slika 5. Ko je kot med položajem in vektorji trdnosti ničen, se navor ne pojavi in ​​zato ni nobenega učinka obračanja. Vir: f. Zapata.

Matematično navor τ Opredeljen je kot vektor ali navzkrižni izdelek med vektorji r (položaj vektor) in F (Sil vektor) slike 5:

Vam lahko služi: statistične veje

τ = r x F

Velikost navora je:

τ = R F Sen θ

Biti θ kot med r in F. Ko je sin θ = 0, je navor ničen, v tem primeru θ = 0 ° (ali tudi 180 °).

Pretok električnega polja

Pretok električnega polja je skalarna velikost, ki je odvisna od intenzivnosti električnega polja, pa tudi od površinske orientacije, skozi katero se prečka.

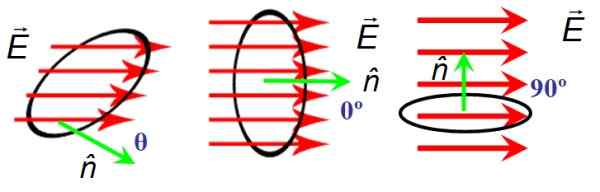
Na sliki 6 je krožna površina površine A, skozi katero prehajajo črte električnega polja In. Površinska orientacija daje običajni vektor n. Na levi strani in običajni vektor tvori akterji poljubni kot θ, v sredini tvorijo ničelni kot in desno so pravokotne.

Kdaj In in n So pravokotne, poljske črte ne prečkajo površine, zato je pretok nič, medtem ko je kot kota med njimi In in n Je praznina, črte popolnoma prečkajo površino.

Označevanje pretoka električnega polja s pomočjo grške črke φ (bere "fi"), njegova definicija za enotno polje, kot je na sliki, ostaja takšen:

Φ = In•nDo

Točka na sredini obeh vektorjev označuje točko ali skalarni izdelek, ki izmenično definira:

Φ = In•nA = eacosθ

Krepke in puščice nad črkam so viri za razlikovanje med vektorjem in njegovo velikostjo, ki je označena z običajnimi črkami. Ker je cos 0 = 1, je pretok največji, ko In in n So vzporedni.

Slika 6. Pretok električnega polja je odvisen od orientacije med površino in električnim poljem. Vir: f. Zapata.

Vaje

- Vaja 1

Dve sili Str in Q Hkrati delujejo na pravočasno objekt x, obe sili sta sprva med njimi θ. Kaj se zgodi z velikostjo nastale sile, ko se θ zmanjša, dokler se ne prekliče?

Vam lahko služi: ocena funkcij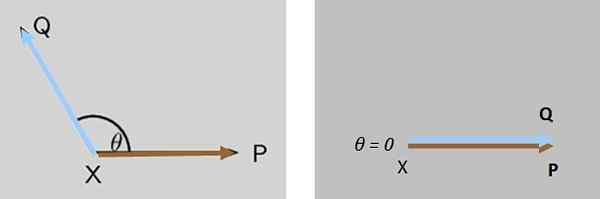 Slika 7. Kot med dvema silama, ki delujeta na telo, se zmanjšuje, dokler velikost nastale sile ne pridobi največje vrednosti v tem primeru. Vir: f. Zapata.

Rešitev

Velikost nastale sile Q + Str Postopoma se povečuje, dokler ni največ, ko Q in Str So popolnoma vzporedni (slika 7 desno).

- Vaja 2

Navedite, ali je ničelni kot rešitev naslednje trigonometrične enačbe:

cos 2x = 1 + 4se x

Rešitev

Trigonometrična enačba je tista, v kateri je neznano del argumenta trigonometričnega razloga. Za rešitev predlagane enačbe je priročno uporabiti formulo za kosinus dvojnega kota:

cos 2x = cos² X - sen² x

Ker na ta način argument na levi strani postane x namesto 2x. Tako:

cos² X - sen² x = 1 + 4sen x

Po drugi strani² X + sen² x = 1, torej:

cos² X - sen² x = cos² X + sen² x + 4sen x

Izraz cos² X je preklican in ostaja:

- Sen² x = sen² x + 4sen x → - 2sen² x - 4senx = 0 → 2sen² x + 4senx = 0

Zdaj je narejena naslednja sprememba spremenljivke: senx = u in enačba se spremeni v:

2U² + 4U = 0

2U (u+4) = 0

Katerih rešitve so: u = 0 in u = -4. Vrnitev spremembe bi imeli dve možnosti: sin x = 0 in senx = -4. Ta zadnja rešitev ni izvedljiva, ker je prsa katerega koli kota med -1 in 1, zato nam ostane prva alternativa:

greh x = 0

Zato je x = 0 ° rešitev, vendar služi tudi kateri koli kot, katerega sinus je 0, kar je lahko tudi 180 ° (π radiani), 360 ° (2 π radianov) in ustrezni negativi tudi tudi negativni.

Najbolj splošna rešitev trigonometrične enačbe je: x = kπ, kjer je k = 0, ± 1, ± 2, ± 3, .. . k celo število.

Reference

1. Baldor, a. 2004. Ravna in vesoljska geometrija s trigonometrijo. Kulturne publikacije s.Do. od c.V. Mehika.
2. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 3. Sistemi delcev. Uredil Douglas Figueroa (USB).
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 5. Električna interakcija. Uredil Douglas Figueroa (USB).
4. Onlinemathlearning. Vrste kotov. Pridobljeno od: onlinemathlearning.com.
5. Zill, d. 2012. Algebra, trigonometrija in analitična geometrija. McGraw Hill Inter -American.