Opis teorema Norton, aplikacije, primeri in vaje

On Nortonski teorem, ki velja za električna tokokroga_Ne povezan vzporedno z odpornostjo r_Ne.

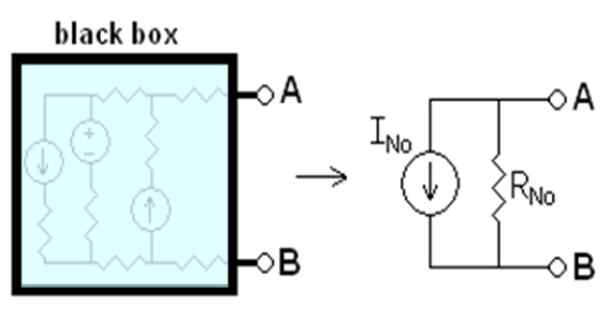
Rekel trenutni i_Ne slišal sem_N To je tisto, ki bi tekel med točkami A in B, če bi bila kratka območja. Odpor R_N To je enakovredna odpornost med terminali, ko so vsi neodvisni viri deaktivirani. Vse rečeno je shematizirano na sliki 1.

Slika 1. Nortonovo ekvivalentno vezje. Vir: Wikimedia Commons. Drumkid [cc by-sa 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Črna škatla na sliki vsebuje linearno vezje, ki ga bo nadomestil njen Norton ekvivalent. Linearno vezje je tisto, v katerem imata vhod in izhod linearno odvisnost, na primer razmerje med napetostjo V in neposrednim tokom I v ohmičnem elementu: V = i.R.

Ta izraz ustreza OHM -ovemu zakonu, kjer je R odpornost, ki je lahko tudi impedanca, če gre za vezje izmeničnega toka.

Nortonov teorem je razvil Electric in izumitelj Edward L inženir. Norton (1898-1983), ki je dolgo delal za Bell Laboratories.

[TOC]

Aplikacije za teorem Norton

Ko imajo zelo zapletene omrežja, z veliko odpornosti ali impedance in želite manjše in bolj obvladljivo vezje.

Na ta način je Nortonov teorem zelo pomemben pri oblikovanju vezij z več elementi, pa tudi pri preučevanju njihovega odziva.

Razmerje med teoremi Nortona in Thevenina

Nortonov teorem je dvojni Theveninov teorem, kar pomeni, da so enakovredni. Theveninov teorem kaže, da lahko črno škatlo na sliki 1 nadomestimo s serijskim napetostnim virom z uporom, imenovano upornost Thevenin r_Th. To je izraženo na naslednji sliki:

Lahko vam služi: Mehanika materiala: Zgodovina, študijsko področje, aplikacije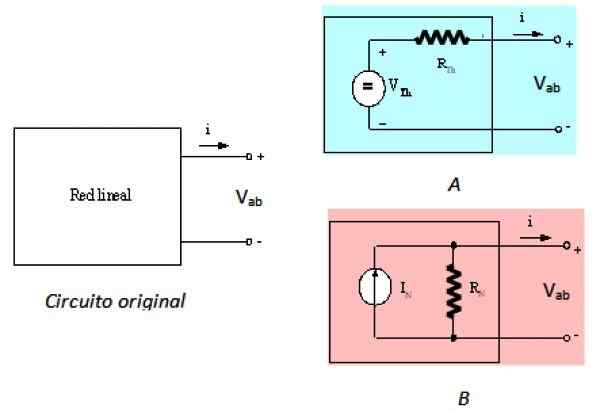 Slika 2. Originalni levi vezje in njegovi ustrezniki Théven in Norton. Vir: f. Zapata.

Levo vezje je originalno vezje, linearno omrežje v črni škatli, vezje na desni je enakovredno theveninovo in vezje B Je Nortonov enakovreden, kot je opisano. Tri vezja, ki jih vidimo iz terminalov A in B, so enakovredni.

Zdaj opazujte, da:

-V originalnem vezju je napetost med sponkami V_Ab.

-V_Ab  = V_Th v vezju Do

-Končno, v_Ab  = I_N.R_N v vezju B

Če sta sponki A in B v treh vezjih kratek stik, je treba izpolniti, da morata biti napetost in tok med temi točkami enaka za tri, saj sta enakovredna. Tako:

-V originalnem vezju je tok i.

-Za vezje A je tok i = v_Th / R_Th, Po OHM -ovem zakonu.

-Končno v vezju B, tok je jaz_N

Zato je sklenjeno, da imata odpornost Nortona in Thevenina enako vrednost in da je tok podan z:

i = i_N = V_Th / R_Th = V_Th / R_N

Primer

Za pravilno uporabo Nortonovega teorema sledimo naslednje korake:

-Odsek vezja, za katerega bo Nortonov ekvivalent na voljo iz omrežja, je izolat iz omrežja.

-V preostalem vezju označite sponke A in B.

-Napeto napetostne vire zamenjajte s kratkimi tokokrogi in trenutnimi z odprtimi vezji, da poiščete enakovredno upor med sponkama A in B. To je r_N.

-Vrnite vse vire na svoje prvotne položaje, kratek krog sponke A in B in poiščite tok, ki kroži med njima. To je jaz_N.

Vam lahko služi: Dopplerjev učinek: opis, formule, primeri, primeri

-Narišite Nortonovo ekvivalentno vezje glede na tisto, kar je prikazano na sliki 1. Oba, trenutni vir in enakovredna odpornost sta vzporedno.

Lahko uporabite tudi Theveninov teorem, da najdete r_Th, za katerega že vemo, da je enak R_N, Potem po Ohmovem zakonu najdete jaz_N In nastalo je vezje.

In zdaj poglejmo primer:

Poiščite Nortonov ekvivalent med točkami A in B naslednjega vezja:

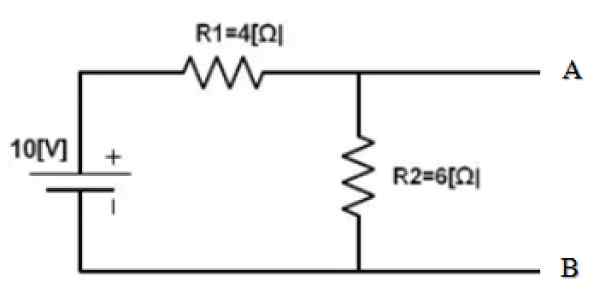Slika 3. Primer vezja. Vir: f. Zapata.

Del vezja je že izoliran, katerega enakovredno je treba najti. In točke A in B sta jasno določena. Sledi, da kratek stik 10 V vir in poiščem enakovredno upornost vezja:

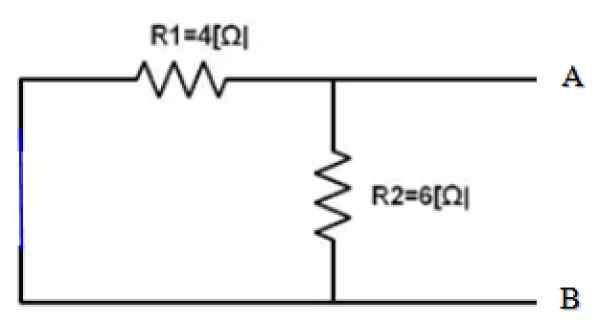Slika 4. Kratek vir. Vir: f. Zapata.

Pogledi iz terminalov A in B, oba upora R₁ in r₂ Zato so vzporedno:

1/r_Eq = 1/r₁₂ = (1/4) + (1/6) ω^-1 = 5/12 Ω^-1  → R_Eq = 12/5 ω = 2.4 Ω

Potem se vir vrne na svoje mesto in točke A in B sta kratka, da bi našli tok, ki kroži tam, to bo_N. V tem primeru:

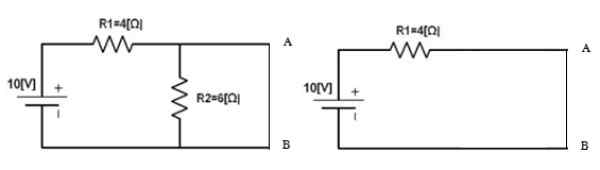Slika 5. Vezje za izračun toka Norton. Vir: f. Zapata.

Yo_N = 10 V / 4 Ω = 2.5 a

Norton ekvivalent

Končno je Nortonov ekvivalent z najdenimi vrednostmi:

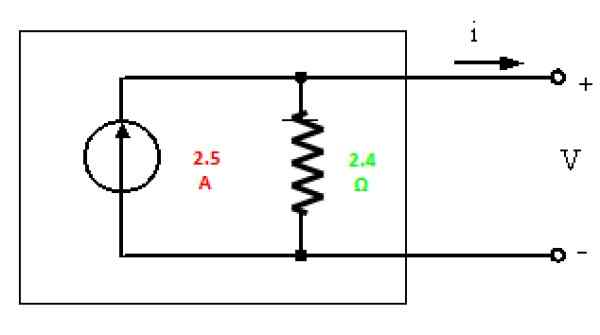Slika 6. Nortonov ekvivalent vezja na sliki 3. Vir: f. Zapata.

Vaja rešena

V vezju naslednje slike:

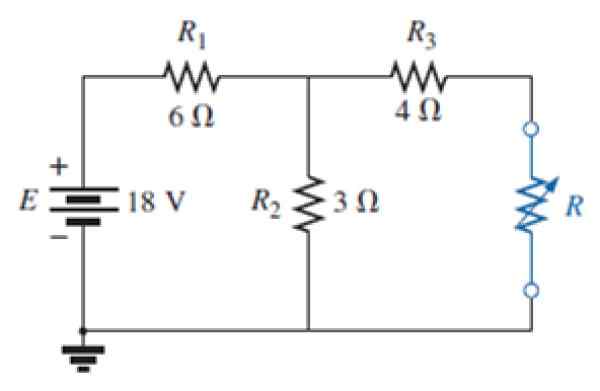Slika 7. Vezje za reševanje vaje. Vir: Aleksander, c. 2006. Temelji električnega vezja. 3. mesto. Izdaja. MC Graw Hill.

a) Poiščite Nortonovo ekvivalentno vezje zunanjega modrega odpornega omrežja.

b) poiščite tudi Théveninov ekvivalent.

Rešitev

Po zgoraj navedenih korakih mora biti vir kratek -krog:

Vam lahko služi: difrakcija zvoka: kaj je sestavljeno iz primerov, aplikacij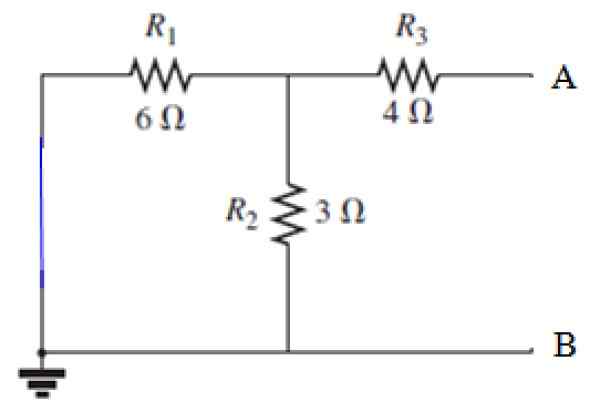 Slika 8. Kratek vir vezja v vezju na sliki 7. Vir: f. Zapata.

RN izračun

Pogled s terminala A in B, odpornost r₃ je v seriji z vzporednico, ki jo tvorijo upori r₁ in r₂, Najprej izračunamo enakovredno odpornost te vzporednice:

1/r₁₂ = (1/6)+ (1/3) ω^-1 = 1/2 Ω^-1  → R_Eq = 2/1 ω = 2Ω

In potem je ta vzporednica v seriji z r_3, tako da je enakovredna odpornost:

R_Eq = 2 Ω + 4 Ω = 6 Ω

To je vrednost obeh r_N od r_Th, Kot je bilo razloženo prej.

Izračun v

Potem sta terminala A in B kratka vezja, ki vir vrnejo na svoje mesto:

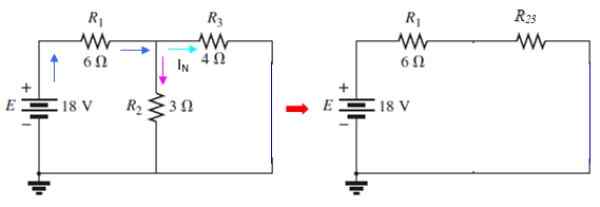Slika 9. Norton tokovni vezji. Vir: f. Zapata.

Tok, ki gre skozi i₃ je tok i_N iskani, ki jih je mogoče določiti z metodo mrežice ali z uporabo serij in vzporednih. V tem krogu r₂ in r₃ So vzporedno:

1/r₂₃ = (1/3)+ (1/4) ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

Odpor R₁ Je v seriji s to vzporednico, nato:

R₁₂₃ = 6 + (12/7) ω = 54/7 Ω

Tok, ki izhaja iz vira (modra barva), izračuna OHM -ov zakon:

V = i. R → i = v/r = 18 V/(54/7 Ω) = 7/3 a

Ta tok je razdeljen na dva dela: enega, ki prečka r₂ In še en, ki prečka r₃. Vendar tok, ki prečka vzporedni r₂₃ Enako je, da gre skozi r₁, Kot je razvidno iz vmesnega vezja slike. Tam je napetost:

V₂₃ = I.R₂₃ = (7/3) a .(12/7) ω = 4 V

Oba upora r₂ in r₃ Zato so v tej napetosti, saj so torej vzporedno:

Yo₃ = V₂₃ / R₃ = 4 V / 4 Ω = 1 a

Že imamo iskan Norton tok, saj kot sem že rekel₃ = I_N, tako:

Yo_N = 1 a

Norton ekvivalent

Vse je pripravljeno, da nariše Norton ekvivalent tega vezja med točkami A in B:

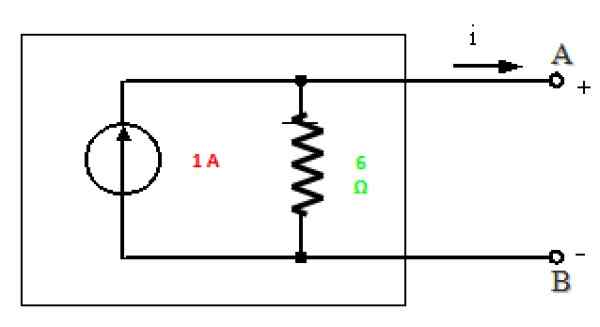Slika 10. Nortonov ekvivalent vezja na sliki 7. Vir: f. Zapata.

Rešitev b

Iskanje Théveninovega ekvivalenta je zelo preprosto, saj r_Th = R_N= 6 Ω in kot je razloženo v prejšnjih razdelkih:

V_Th = I_N. R_N = 1 a . 6 Ω = 6 V

Théveninovo ekvivalentno vezje je:

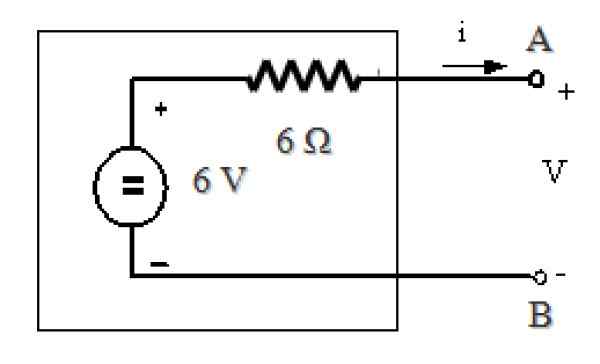Slika 11. Eveninov ekvivalent vezja na sliki 7. Vir: f. Zapata.

Reference

1. Aleksander, c. 2006. Temelji električnega vezja. 3. mesto. Izdaja. MC Graw Hill.
2. Boylestad, r. 2011. Uvod v analizo vezja. 2. mesto. Izdaja. Pearson.
3. Dorf, r. 2006. Uvod v električne kroženja. 7. Izdaja. John Wiley & Sons.
4. Edminister, j. Devetnajst devetdeset šest. Električna vezja. Serija Schaum. 3. mesto. Izdaja. MC Graw Hill.
5. Wikipedija. Nortonski teorem . Okrevano od: je.Wikipedija.org.