Quadrilateralni elementi, lastnosti, klasifikacija, primeri

A kvadrilateralno To je štiristranski poligon in štiri točke. Njihove nasprotne strani Oni so tisti, ki nimajo skupnih točk, medtem ko so zaporedne strani Tisti, ki imajo skupno točko.

V štirikotniku so sosednji koti Tisti, ki delijo stran nasproti kotov Nimajo skupnih strani. Druga pomembna značilnost štirikotnika je, da je vsota njegovih štirih Notranji koti To je dvakrat ravni kot, to je 360 ​​° ali 2π radianov.

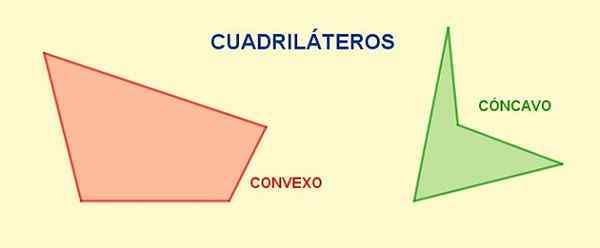
Slika 1. Različni štirikolesniki. Vir: f. Zapata.

Diagonale So segmenti, ki združujejo točko s svojim nasprotnim in v določenem obroču, z vsake točke lahko narišete eno diagonalo. Skupno število diagonalov kvadrilateralne je dve.

Quadrilaterals so osebe, ki jih človeštvo pozna že od antičnih časov. To potrjujejo arheološke zapise in konstrukcije, ki preživijo danes.

Tudi danes imajo štirikolesniki še vedno pomembno prisotnost v vsakdanjem življenju. Bralec lahko ta obrazec najde na zaslonu, na katerem besedilo bere v tem natančnem trenutku, v oknih, vratih, avtomobilskih delih in neštetih krajih več več.

[TOC]

Klasifikacija štirikotnikov

Glede na vzporednico nasprotnih strani so štirikolesniki razvrščeni na naslednji način:

1. Trapezoid, Kadar ni vzporednic in je štirikotnik izbočen.
2. Trapez, Ko obstaja vzporednica med enim parom nasprotnih strani.
3. Paralelogram, Ko so njihove nasprotne strani vzporedne dve do dva.

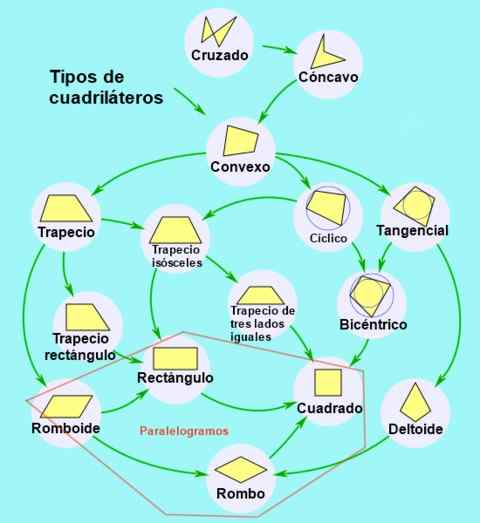Slika 2. Razvrstitev in podklasifikacija štirikotnikov. Vir: Wikimedia Commons.

Vrste paralelograma

Paralelograme je mogoče razvrstiti glede na njihove kote in strani, kot sledi:

1. Pravokotnik, To je paralelogram, ki ima štiri notranje kote enakega merila. Notranji koti pravokotnika tvorijo desni kot (90 °).
2. Kvadrat, Je pravokotnik s štirimi stranicami enakega merila.
3. Diamant, Je paralelogram s svojimi štirimi stranicami, vendar so različni sosednji koti.
4. Rhomboid, paralelogram z različnimi sosednjimi koti.

Trapez

Trapez je konveksni štirikotnik z dvema vzporednima stranicama.

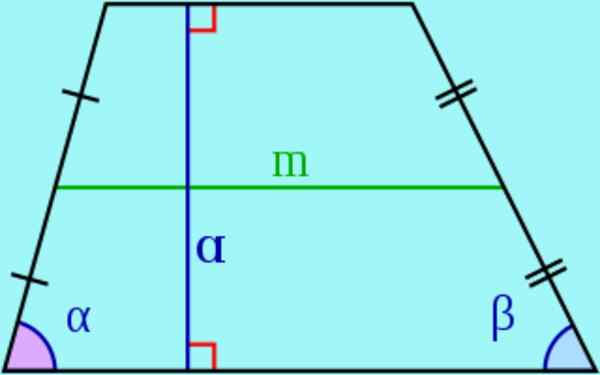Slika 3. Baze, stranska, višina in srednja trapeza. Vir: Wikimedia Commons.

- V trapez se imenujejo vzporedne strani baze In ne -paraleli se imenujejo bočna.

- The višina trapeza je razdalja med obema podlagama, to je dolžina segmenta s konci v podstavkih in pravokotno na isto. Ta segment se imenuje tudi višina trapeze.

- The mediana Segment se pridruži sredinskim točkam strani. Lahko je dokazano, da je mediana vzporedna z osnovami trapeza in njena dolžina je enaka poltomerjem baz.

- Območje trapeza je njegova višina, pomnožena s poltezami baz:

Površina trapeze = višina * (osnova 1 + podlaga 2) / 2

Vrste trapeza

-Pravokotnik trapez: To je tisti, ki ima stran pravokotno na podlagi. Ta stran je tudi višina trapeza.

-Trapezijevi izosceles: Tista z enakimi dolžinami. V izosceles trapezu so koti, ki mejijo na baze, enaki.

-Escaleno Trapezio: Tisti, ki ima svoje strani različne dolžine. Njegovi nasprotni koti so lahko akutni in drugi obljudni, vendar se lahko zgodi tudi, da sta oba obrobna ali oba akutna.

Vam lahko služi: rešene faktorizacijske vaje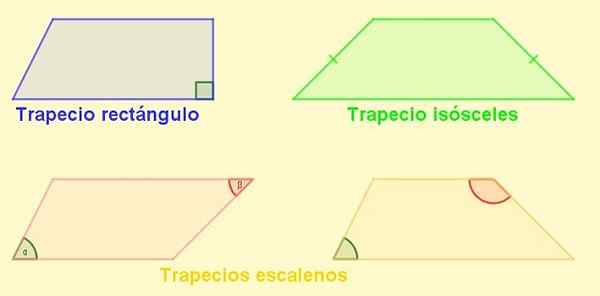 Slika 4. Vrste trapeza. Vir: f. Zapata.

Paralelogram

Paralelogram je kvadrilateralen, katerih nasprotne strani so vzporedne dve do dva. V paralelogramu so nasprotni koti enaki in sosednji koti so dopolnilni ali z drugimi besedami, sosednji koti skupaj 180 °.

Če ima paralelogram pravi kot, bodo tudi vsi drugi koti in posledična slika se imenuje pravokotnik. Če pa ima pravokotnik tudi sosednje strani iste dolžine, potem so vse njegove strani enake in nastala številka je kvadrat.

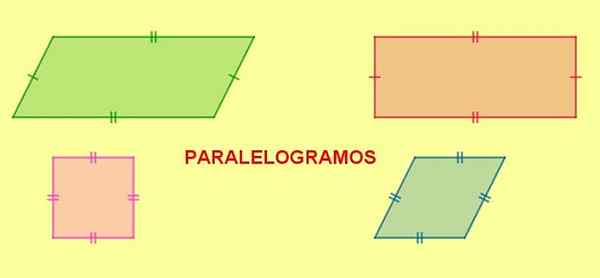Slika 5. Paralelogrami. Pravokotnik, kvadrat in romb so paralelogrami. Vir: f. Zapata.

Ko ima paralelogram dve sosednji strani iste dolžine, bodo vse njene strani enake dolžine in posledična slika je a diamant.

Višina paralelograma je segment s konci na nasprotnih straneh in nanje pravokotno.

Območje paralelograma

Površina paralelograma je produkt podstavka po njegovi višini, podlaga pa je stranska pravokotna na višino (slika 6).

Območje paralelograma = osnovna x višina = a . h

Diagonale paralelograma

Kvadrat diagonale, ki se začne z vrhove, je enak vsoti kvadratov obeh strani, ki mejijo na omenjeno vrhovo, bolj dvojni produkt teh strani s kosinusom kota tega vrha:

F² = a² +  d² + 2 a d cos (α)

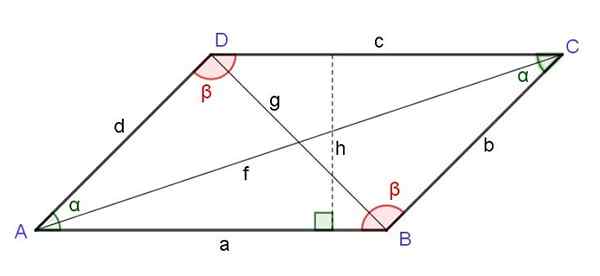Slika 6. Paralelogram. Nasproti kotov, višine, diagonale. Vir: f. Zapata.

Kvadrat diagonale, ki nasprotuje točki paralelograma, je enak vsoti kvadratov obeh strani, ki mejijo na omenjeno točko, in je dvojni produkt teh strani odšteval s kosinusom kota tega vrha:

g² = a² + d² - 2 a d cos (α)

Zakon o paralelogramih

V katerem koli paralelogramu je vsota kvadratov njihovih strani enaka vsoti kvadratov diagonal:

do² + b² + c² + d² = f² + g²

Oferictangle

Pravokotnik je štirikolesnik z nasprotnimi stranicami, vzporednimi dvema do dvema in ima tudi pravi kot. To pomeni, da je pravokotnik vrsta paralelograma z desnim kotom. Za paralelogram, Pravokotnik ima svoje nasprotne strani enake dolžine A = C in B = D. 

Toda kot v katerem koli paralelogramu sosednje kote so dodatni in enaki nasprotni koti, v pravokotniku, če ima pravi kot, bo nujno tvoril ravne kote v drugih treh kotih. To pomeni V pravokotniku vsi notranji koti merijo radiane 90 ° ali π/2.

Diagonale pravokotnika

V pravokotniku so diagonale enake dolžine, Kot bo prikazano spodaj. Obrazložitev je naslednji; Pravokotnik je paralelogram z vsemi ravnimi koti in zato podeduje vse lastnosti paralelograma, vključno s formulo, ki daje dolžino diagonalov:

F² = a²+  d² + 2 a d cos (α)

g² = a² + d² - 2 a d cos (α)

z α = 90 °

Kot Cos (90 °) = 0, Torej se zgodi, da:

F² = g² = a² +  d²

To je f = g, in torej dolžine F in g Od obeh diagonalov pravokotnika sta enaki, njihova dolžina pa je podana z:

Diagonalna dolžina pravokotnika = √ (a² + b²)

Poleg tega, če v pravokotniku sosednjih strani do in b Ena stran temelji na drugi strani višina in posledično bo območje pravokotnika:

Lahko vam služi: Fibonacci Series: Lastnosti, naravni odnosi, aplikacije

Območje pravokotnika = a x b.

Obod je vsota vseh strani pravokotnika, a ker so nasprotja enaka, je potem potreben za stranski pravokotnik do in b Obod je podan z naslednjo formulo:

Pravokotnik Perimeter = 2 (A + B)

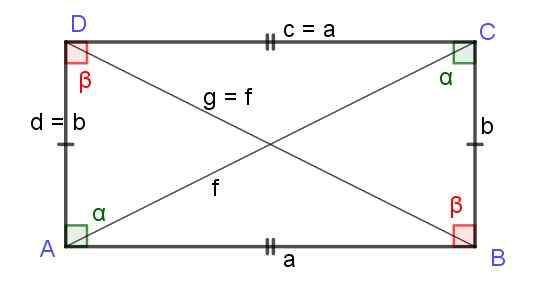Slika 7. Pravokotnik strani A in B. Diagonale F in G sta enaki dolžini. Vir: f. Zapata.

Kvadrat

Trg je pravokotnik s sosednjimi stranicami iste dolžine. Če ima kvadrat stran do, Nato njegove diagonale F in g Imajo enako dolžino, kar je F = g = (√2) a.

Območje kvadrata je njegova stran, dvignjena na kvadrat:

Površina kvadrata = a²

Obod kvadrata je dvakrat ob strani:

Obod kvadrata = 4 a

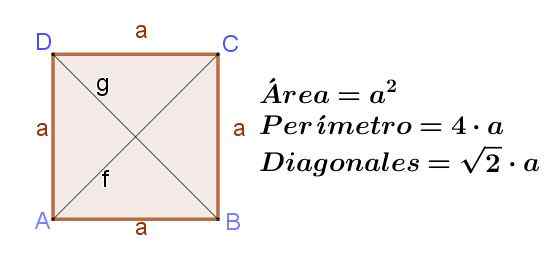Slika 8. Kvadratno do strani A, kar kaže na njegovo območje, obod in dolžino diagonalov. Vir: f. Zapata ..

Diamant

Rhomb je paralelogram s sosednjimi stranicami iste dolžine, toda kot v paralelogramu so tudi nasprotne strani enake, Vse strani rombusa so enake dolžine.

Diagonale romba so različne dolžine, vendar so rezane pod pravim kotom.

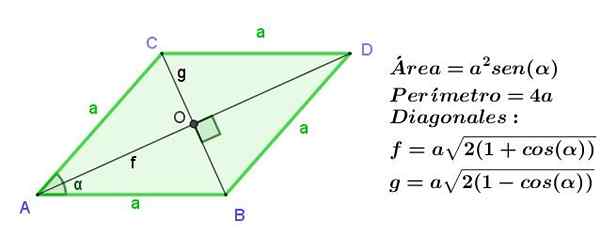Slika 9. Rhombus s strani A, kar kaže na njegovo območje, obod in dolžino njegovih diagonalov. Vir: f. Zapata.

Primeri

Primer 1

Dokažite, da v štirikotniku (ne prekrižani) notranji koti skupaj 360 °.

Slika 10: Prikazana je kot vsota kotov kvadrilateralnega dodajanja 360 °. Vir: f. Zapata.

ABCD velja za ABCD (glej sliko 10) in narisana je diagonalna BD. Oblikovana sta dva trikotnika ABD in BCD. Vsota notranjih kotov ABD trikotnika je:

α + β₁ + δ₁ = 180 °

In vsota notranjih kotov trikotnika BCD je:

 β2 + γ + δ₂ = 180 °

Dodajanje obeh enačb se dobi:

α + β₁ + δ₁ +  β₂ + γ + δ₂ = 180 ° + 180 °

Združevanje:

α + (β₁ +  β₂) + (δ₁ + δ₂) + γ = 2* 180 °

Združevanje in odmevanje je končno dokazano, da:

α + β + Δ + γ = 360 °

Primer 2

Dokažite, da je mediana trapezoida vzporedna z njegovimi osnovami, njegova dolžina.

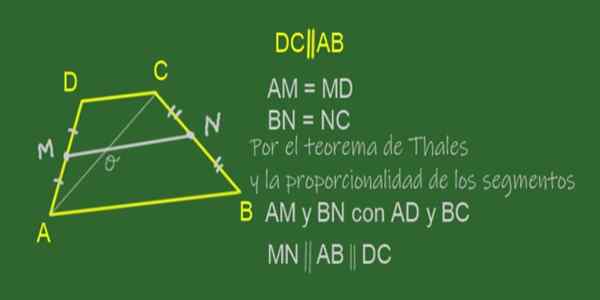Slika 11. Srednja MN ABCD trapeze. Vir: f. Zapata.

Mediana trapeza je segment, ki se pridružuje sredinskim točkam svojih strani, to je ne -Paralelne strani. V trapez ABCD, prikazani na sliki 11, je mediana Mn. 

Ker gre za srednjo točko AD in N Mid BC Point, je izpolnjeno, da sta količina AM / AD in BN / BC enaka.

To pomeni, da je AM sorazmeren BN v enakem deležu kot AD je BC, zato so pogoji za uporabo teorema (vzajemnega) talesa, ki potrjujejo naslednje:

"Če sta v treh ali več ravnih rezanih dveh sekatu".

V našem primeru je sklenjeno, da so črte MN, AB in DC vzporedne med seboj:

»LV mediani je ena od trapez vzporedna z njegovimi osnovami".

Vam lahko služi: kombinirane operacije

Zdaj bo veljal Thalesov teorem:

"Nabor vzporednic, ki jih razrežemo dve ali več sušenja, določite proporcionalne segmente".

V našem primeru AD = 2:00, AC = 2 AO, tako da je trikotnik DAC podoben MAO trikotniku in posledično DC = 2 meseca.

Podoben argument omogoča potrditev, da je Cu podoben CON, kjer sta Ca = 2 CO in CB = 2 CN. Sledi, da AB = 2 naprej.

Skratka, ab = 2 na y 2 meseci. Torej, ko smo odšli:

AB + DC = 2 ON + 2 MO = 2 (MO + ON) = 2 Mn

Končno razčisti MN:

Mn = (AB + DC) /2

In sklepano je, da mediana trapeza meri poldele baz ali z drugimi besedami: mediana meri vsoto baz, deljeno z dvema.

Primer 3

Dokažite, da so v rombusu diagonale rezane pod pravim kotom.

Slika 12. Rhombus in demonstracija, da so njihove diagonale rezane pod pravim kotom. Vir: f. Zapata.

Odbor na sliki 12 prikazuje potrebno konstrukcijo. Najprej je ABCD paralelogram narisan z AB = BC, to je romb. Diagonale AC in DB določajo osem kotov, prikazanih na sliki.

Z uporabo teorema (a.Yo.str.), ki navaja, da notranji nadomestni koti med vzporednicami, ki jih razreže secant, določajo enake kote, lahko vzpostavimo naslednje:

α₁ = γ₁, α2 = γ2, δ₁ = Β₁ in Δ2 = β2. (*)

Po drugi strani, ker so sosednje strani rombusa enake dolžine, se določijo štirje trikotniki izosceles:

DAB, BCD, CDA in ABC

Zdaj se uveljavlja teorem trikotnikov (izosceles), ki navaja, da so koti, ki mejijo na bazo, enake mere, kjer je sklenjeno, da:

δ₁ = β2, Δ2 = β₁, α2 = γ₁ in α₁ = γ2 (**)

Če sta razmerja (*) in (**) združeni, je dosežena naslednja enakost kotov:

α₁ = α2 = γ₁ = γ₁ Na eni strani in β₁ = Β2 = δ₁ = Δ2 za drugo. 

Spominjanje teorema enakih trikotnikov, ki potrjuje, da sta dva trikotnika z enakimi stranmi med dvema enakima kotom enaka:

Aod = aob in posledično tudi koti ∡aod = ∡aob.

Potem ∡aod + ∡aOB = 180 °, a ker sta oba kota enaka, 2 ∡aod = 180 °, kar pomeni, da je ∡aod = 90 °.

To pomeni, da geometrijsko dokazujemo, da so diagonale romba rezane pod pravimi koti.

Vaje rešene

- Vaja 1

Dokažite, da so v pravokotniku trapezoid koti ne-EG dopolnilni.

Rešitev

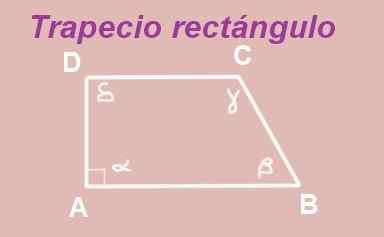Slika 13. Pravokotnik trapez. Vir: f. Zapata.

ABCD Trapezoid je zgrajen z vzporednimi bazami AB in DC. Notranji kot vrha A je raven (meri 90 °), zato imate trapezoid pravokotnik.

Kota α in δ sta notranji koti med dvema vzporednima vzporednicama AB in DC, zato sta enaki, to je Δ = α = 90 °. 

Po drugi strani se je pokazalo, da vsota notranjih kotov štirikotnika doda 360 °, to je:

α + β + γ + Δ = 90º + β + 90º + δ = 360 °.

Zgoraj vodi do:

 β + Δ = 180 °

Potrditev, kaj želi dokazati, da sta kota β in Δ dopolnila.

- Vaja 2

Paralelogram ABCD ima AB = 2 cm in AD = 1 cm, poleg tega pa je kot slabi 30 °. Določite območje omenjenega paralelograma in dolžino njegovih dveh diagonalov.

Rešitev

Območje paralelograma je produkt dolžine njegove baze po višini. V tem primeru bo dolžina segmenta B = AB = 2 cm vzeta kot podlaga, druga stran ima dolžino a = ad = 1 cm in višina h bo izračunana na naslednji način:

H = ad * sin (30 °) = 1 cm * (1/2) = ½ cm.

Potem: območje = b * h = 2 cm * ½ cm = 1 cm².

Reference

1. C. In. Do. (2003). Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Uredniška skupina Patria.
3. Osvobojen, k. (2007). Odkrijte poligone. Benchmark Education Company.
4. Hendrik, v. (2013). Splošni poligoni. Birkhäuser.
5. Iger. (s.F.). Matematika Prvi semester Tacaná. Iger.
6. Jr. Geometrija. (2014). Poligoni. Lulu Press, Inc.
7. Miller, Heeren in Hornsby. (2006). Matematika: sklepanje in aplikacije (deseta izdaja). Pearson Education.
8. Patiño, m. (2006). Matematika 5. Uredništvo Progreso.
9. Wikipedija. Quadrilateral. Okrevano od: je.Wikipedija.com