Merila podobni trikotniki

Kakšna so merila podobnosti trikotnikov?

Merila za podobnost trikotnikov so pravila, ki omogočajo vedeti, ali sta dva trikotnika podobna. Podobnost geometrijskih figur, vključno s trikotniki, zahteva, da imajo številke na enak način, čeprav nimajo nujno enake ali enake orientacije.

Da bi bila dva trikotnika podobna, je treba: i) njihove homologne strani so sorazmerne in ii) Notranji koti vsakega imajo enak ukrep.

Slika 1. Dva podobna trikotnika: Čeprav nimata enake velikosti, so njihove strani sorazmerne in njihovi notranji koti imajo enako mero. Vir: f. Zapata.

Proporcionalno razmerje ali delež med dvema količinama A in B je predstavljeno z razmerjem A/B, z B ≠ 0. Za podobne trikotnike so veljavni naslednji deleži med stranicami:

a/a '= b/b' = c/c '= r

Vrednost r se imenuje Razlog podobnosti.

Poleg tega morajo biti ustrezni notranji koti istega ukrepa, torej: ∠a = ∠a '; ∠B = ∠B 'in ∠C = ∠C'. V skladu s temi pogoji so merila podobnosti trikotnikov:

Merila 1: Dva trikotnika sta podobna, če imata dva notranja kota enakega merila. Če je tako, tudi tretji kot meri enako, saj je vsota notranjih kotov v katerem koli trikotniku 180 °:

α = α '; β = β '

Merila 2: Trikotniki so podobni, če sta dve homologni strani sorazmerni in je kot med njima enak:

a/a '= b/b'; α = α '

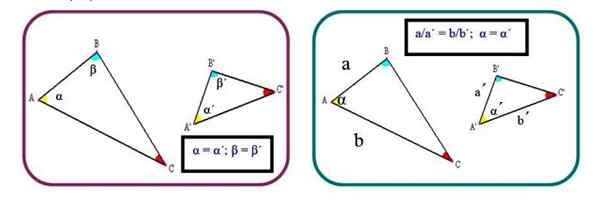Slika 2. Dva merila za določitev podobnosti trikotnikov. Vir: f. Zapata.

Merila 3: Tri homologne strani so sorazmerne:

a/a '= b/b' = c/c '= r

Primeri

Podobnost trikotnikov je zelo uporabna za izračun višin in razdalj, ki jih ni enostavno neposredno meriti neposredno. Z nekaj preprostimi izračuni je mogoče te dolžine mogoče ugotoviti s primerjavo podobnih trikotnikov.

Vam lahko služi: temeljni teorem aritmetike: demonstracija, aplikacije, vaje

Višina stolpcev, zgradb in dreves

Govori se, da je oče geometrije v starodavni Grčiji, kot je Miletus (625-547 do.C.), izračunal višino stolpca templja brez potrebe po posebnih instrumentih, preprosto primerjal dolžino sence svojega trsa z dolžino stolpca in uporabil podobnost trikotnikov. Z isto metodo mu je uspelo izmeriti višino velike egiptovske piramide in tako navdušil faraona.

Razdalja do lune

Obstaja preprost eksperiment, ki se izvaja za izračun razdalje med zemljo in luno. Zahteva valuto, malo lepilnega traku in vernirja ali diplomiranega pravila. Ko je luna polna, je valuta pritrjena na kozarec okna in luna opazimo z enim očesom, ki se nahaja tako, da valuta pokriva samo polno luno.

Ko se to zgodi, je razlog med premerom valute in razdaljo med očesom in valuto enak, kot je med premerom lune in razdaljo med očesom in luno:

Premer valute/razdalja valuta = premer lune/razdalja do lune

Razlog je približno 1/110. Kar pomeni, da je razdalja do lune 110 -krat večja od premera tega.

Trenutno je polmer lune ocenjen leta 1737.1 km, tako da je njegov premer 3474.2 km. Z zamenjavo te vrednosti v razmerju:

Razdalja do lune = premer lune ÷ (premer valute/razdalja do valute)

Je pridobljeno:

Razdalja do lune = 3474.2 km ÷ (1/110) = 382.162 km

Lahko vam služi: hepagonska prizma

Zelo blizu vrednosti, ki jo je vzpostavilo 384 astronomov.000 km.

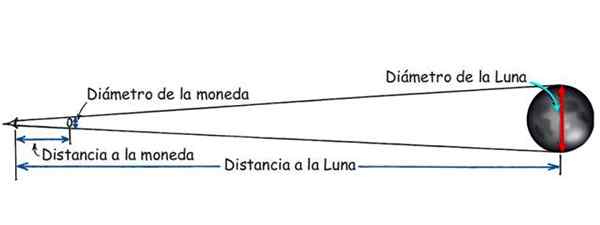Slika 3. Razdalja do Lune je lahko znana po zaslugi podobnosti trikotnikov. Vir: Modified Hewitt, P. Konceptualna fizika.

Razdalja med ladjo in obalo

Za merjenje razdalje med ladjo in obalo so vložki zataknjeni na plaži v točkah A, B, C in Q. Trikotniki ABC in PCQ so podobni po merilih 1, saj imata dva enaka kota: dva kota ∠C = α, ki nasprotujeta točki in dva ravna kota, enaka 90 °: ∠B = ∠Q.

Dva trikotnika, ki se nahajata na ta način Thalesov položaj In so vedno podobni. Trikotniki so identificirani v položaju Thalesa za skupni kot in nasprotne strani pod tem kotom so vzporedne.

V naslednjem razdelku je vaja s številčnimi vrednostmi.

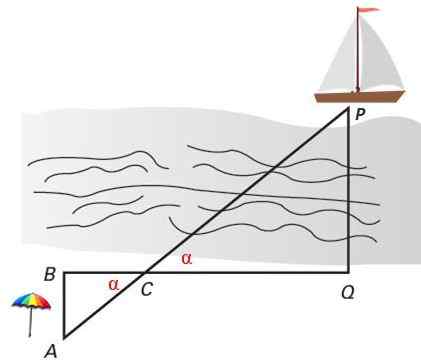Slika 4. Dva podobna trikotnika v položaju Thalesa služita za izračun pravokotne razdalje ladje na obalo. Vir: f. Zapata.

Rešene vaje

Vaja 1

Želite ugotoviti, kako daleč je jadrnica zasidrana na prejšnji sliki, od točke, ki se nahaja na obali plaže, za katero so vložki prikovani v točkah A, B, C in Q, s čimer določite trikotnik ABC je podoben PCQ, vendar jih je lažje izmeriti strani.

Izračunajte pravokotno razdaljo PQ med ladjo in obalo s podobnostjo trikotnikov, če so razdalje, ki so na voljo,:

AB = 12 m

BC = 16 m

QC = 60 m

Rešitev

Delež med homolognimi stranicami je:

Ab/qp = bc/cq = 16 m/60 m = 0.267

Zato 0.267 je razlog za podobnost:

AB/QP = 0.267

QP = AB / 0.267 = 12 m / 0.267 = 44.9 m

Vaja 2

V naslednjem trikotniku: koliko meri segment oglasov?

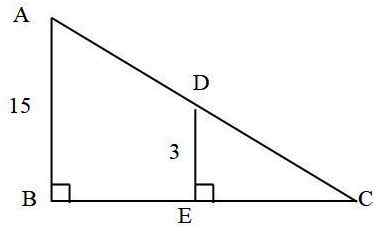
Znano je, da:

• AC = 25 cm
• AB = 15 cm
• De = 3 cm

Vam lahko služi: večkratniki 2: kaj so in razlaga

Rešitev

Trikotniki so podobni, saj imajo kota, ki je ∠c in strani in ab sta vzporedni. Razmerje podobnosti se izračuna z:

R = ab / de = 15 cm / 3 cm = 5

In tudi skozi:

R = AC / DC

Zato dc = AC / R = 25 cm / 5 = 5 cm

Od:

AC = AD + DC

Iz tega sledi, da ad = ac - dc = 25 cm - 5 cm = 20 cm

Vaja 3

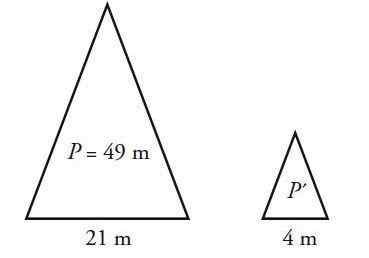
Trikotnik izosceles ima obod 49 cm in osnovo 21 cm. Izračunajte obod trikotnika, podoben temu, vendar njihov baza meri 4 cm.

Rešitev

Trikotnik Isosceles ima dve enaki strani, ki se razlikujejo od baze B. Naj bo ℓ merilo strani in p oboda, ki je sestavljen iz vsote treh strani. Za največji trikotnik:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Zdaj se dvigne delež med stranicami trikotnikov, tisti iz majhnega trikotnika so simbolizirani s premijami:

B/ b '= ℓ/ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

Obod majhnega trikotnika bo:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Reference

1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
2. Hewitt, Paul. 2012. Konceptualna fizikalna znanost. 5. Ed. Pearson.
3. Clemens, s. Geometrija z aplikacijami. Addison Wesley.
4. Ibáñez, str. 2010. Matematika III. Cengage učenje.
5. Jiménez, r. Matematika II: geometrija in trigonometrija. 2. mesto. Izdaja. Pearson.
6. Stewart, J. 2007. Prekalenkulacija. 5. Izdaja. Cengage učenje.
7. Vicmat. Samos Aristarco: Ukrepi sončnega sistema. Okreval od: vicmat.com