Sferične koordinate primere in rešene vaje

The sferične koordinate So točkovni sistem lokacije v tridimenzionalnem prostoru, ki ga sestavljajo radialna koordinata in dve kotni koordinati, imenovani polarna koordinata in azimutalna koordinata.

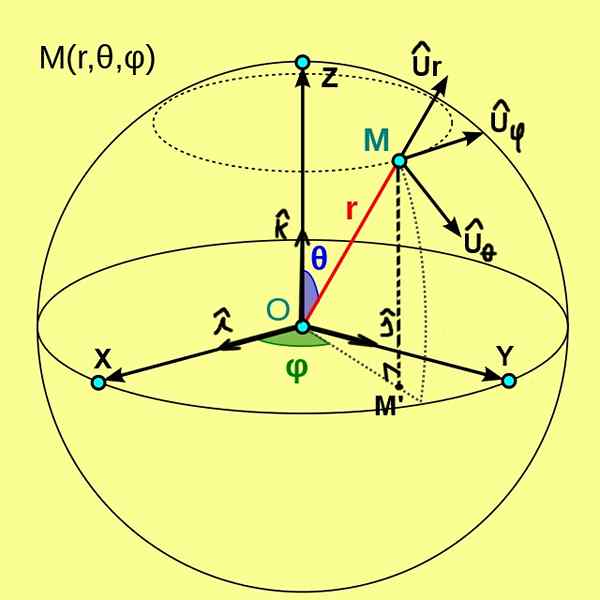
Na sliki 1, ki jo vidimo spodaj, so prikazane sferične koordinate (r, θ, φ) točke m. Te koordinate se nanašajo na ortogonalni sistem kartezijanskih osi x, y, z izvora ali.

Slika 1. Sferične koordinate (r, θ, φ) iz točke m. (Wikimedia Commons)

V tem primeru je koordinata r točke m razdalja od te točke do izvora oz. Polarna koordinata θ predstavlja kot med pozitivno poloki Z in polmerom vektorja OM. Medtem ko je azimutalna koordinata φ kot med pozitivno poloki X in vektorskim polmerom OM ', saj je m' ortogonalna projekcija m na ravnini xy.

Radialna koordinata R ima le pozitivne vrednosti, če pa je točka nameščena na izvoru, potem r = 0. Polarna koordinata θ traja kot najmanjša vrednost 0 ° za točke, ki se nahajajo na pozitivnem pol -tribu. Končno, azimutalna koordinata φ sprejme kot najmanjša vrednost 0 ° in največ 360 °.

0 ≤ r < ∞

0 ≤ θ ≤ 180 °

0 ≤ φ  < 360º

[TOC]

Sprememba koordinat

Nato bodo podane formule, ki omogočajo kartezijanske koordinate (x, y, z) točke m, ob predpostavki, da so sferične koordinate iste (r, θ, φ) točke:

x = r sen (θ) cos (φ)

y = r sen (θ) greh (φ) 

z = r cos (θ)

Na enak način je koristno najti odnose, ki se premikajo iz kartezijanskih koordinat (x, y, z) točke, ki jih daje sferične koordinate te točke:

R = √ (x^2 + y^2 + z^2)

θ = Arcan (√ (x^2 + y^2) / z)

Vam lahko služi: diskretna naključna spremenljivka

φ = arctan (y / x)

Vektorska baza v sferičnih koordinatah

Iz sferičnih koordinat je opredeljena ortonormalna baza osnovnih vektorjev, ki jih označuje Ur, Uθ, Uφ. Slika 1 prikazuje te tri enotne vektorje, ki imajo naslednje značilnosti:

- Ur To je enota vektorska tangenta do radialne črte θ = ctte in φ = ctte;

- Uθ To je enotni tangentni vektor za lok φ = ctte in r = ctte;

- Uφ To je enotna vektorska tangenta za lok r = ctte in θ = ctte.

Elementi linij in glasnosti v sferičnih koordinatah

Vektorski položaj točke v vesolju v sferičnih koordinatah je napisan tako:

r = r Ur

Toda neskončno majhna variacija ali premik točke v tridimenzionalnem prostoru v teh koordinatah je izražena z naslednjim vektorskim razmerjem:

dr = dr Ur + r dθ Uθ + r sen (θ) dφ Uφ

Končno je napisan neskončni volumen DV v sferičnih koordinatah tako:

dv = r^2 sin (θ) dr θ dφ

Ta razmerja so zelo koristna za izračun linijskih integralov in glasnosti v fizičnih situacijah, ki imajo sferično simetrijo.

Odnos z geografskimi koordinatami

Geografske koordinate se razume, da služijo za iskanje krajev na zemeljski površini. Ta sistem uporablja koordinate širine in dolžine za iskanje položaja na površini zemlje.

V geografskem koordinatnem sistemu naj bi bila zemeljska površina.

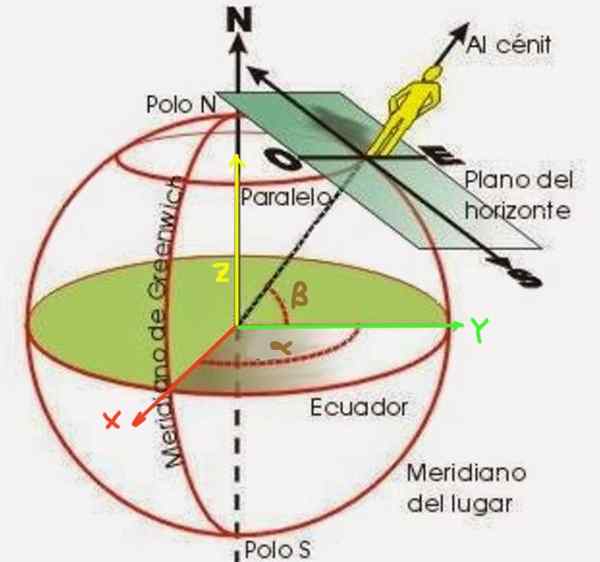Slika 2. Dolžina α in β širina opazovalca na zemeljski površini.

Β širina je kot, ki ga tvori polmer, ki se začne od središča zemlje do točke, ki jo želite postaviti. Izmeri se iz ekvatorialne ravnine, kot je prikazano na sliki 2. Po drugi strani je dolžina α kot, ki ga poldnevnik točke, ki postavlja obliko glede na ničelni poldnevnik (znan kot Greenwich Meridian).

Vam lahko služi: relativna vrednost

Širina je lahko severna ali južna širina, odvisno od tega, ali je kraj, ki se nahaja, na severni polobli ali na južni polobli. Podobno je lahko dolžina zahodna ali to, odvisno od tega, ali je lokacija zahodno ali vzhodno od ničle Meridian.

Formule za spremembo iz geografske v sferične

Za pridobitev teh formul je prva stvar vzpostaviti koordinatni sistem. XY ravnina je izbrana, ki sovpada z ekvatorialno ravnino, ki je pozitivna poloka x, ki sega iz središča zemlje in skozi ničlo pod poldnevnikom. Osi in prehaja skozi 90 ° in Meridian. Zemljina površina ima RT radio.

S tem koordinatnim sistemom so torej geografske in sferične transformacije:

αEβn → (RT, θ = 90 °-β, φ = α)

αβN → (RT, θ = 90º-β, φ = 360 °-α)

αEβ → (RT, θ = 90 °+β, φ = α)

αoβs → (RT, θ = 90 °+β, φ = 360 °-α) 

Primeri

Primer 1

Geografske koordinate Palma de Mallorca (Španija) so:

Vzhodna dolžina 38.847 ° in severna širina 39.570 °. Za določitev sferičnih koordinat, ki ustrezajo Palma de Mallorca, se uporablja prva formula iz prejšnjega oddelka formul:

38,847ºE39,570ºn → (r = 6371 km, θ = 90 °-39,570 °, φ = 38,847 °)

Potem so sferične koordinate:

Palma de Mallorca: (r = 6371 km, θ = 50,43 °, φ = 38,85 °)

V prejšnjem odgovoru je bil odvzet R enak povprečnemu polmeru Zemlje.

Primer 2

Če veste, da imajo Falklandski otoki (Falkland) geografske koordinate 59 ° O 51,75 ° S, določite ustrezne polarne koordinate. Ne pozabite, da osi X preide od središča zemlje do poldnevnika 0 ° in na ekvatorialni ravnini; Os y tudi v ekvatorialni ravnini in skozi 90 ° zahodni poldnevnik; Končno os Z na osi zemeljskega vrtenja v smeri južno-severnega.

Vam lahko služi: curtoza: definicija, vrste, formule, za kaj je na primer

Če želite nato najti ustrezne sferične koordinate, uporabljamo formule, predstavljene v prejšnjem razdelku:

59ºO 51,75ºS → (r = 6371 km, θ = 90 °+51,75 °, φ = 360 °-59 °), torej

Malvinas: (r = 6371 km, θ = 141,75 °, φ = 301 °)

Vaje

Vaja 1

Poiščite kartezijanske koordinate Palma de Mallorca v referenčnem sistemu Cartesiano XYZ, prikazano na sliki 2.

Rešitev: Prej so bile v primeru 1 pridobljene sferične koordinate na podlagi geografskih koordinat Palma de Mallorca. Tako da se zgoraj predstavljene formule lahko uporabijo za prehod iz sferične na kartezijane:

x = 6371 km sen (50,43 °) COS (38,85 °)

Y = 6371 km sen (50,43 °) Sen (38,85 °) 

Z = 6371 km cos (50,43 °)

Izvajanje ustreznih izračunov je:

Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)

Vaja 2

Poiščite kartezijanske koordinate Falklandskih otokov v referenčnem sistemu Cartesiano XYZ, prikazano na sliki 2.

Rešitev: Prej v primeru 2 so bile sferične koordinate pridobljene na podlagi geografskih koordinat Falklandskih otokov. Tako da se zgoraj predstavljene formule lahko uporabijo za prehod iz sferične na kartezijane:

x = 6371 km sen (141,75 °) COS (301 °)

y = 6371 km sen (141,75 °) Sen (301 °) 

Z = 6371 km cos (141,75 °)

Izvedba ustreznih izračunov se dobi:

Falklandski otoki: (x = 2031 km, y = -3381 km, z = -5003)

Reference

1. Arfken g in weber h. (2012). Matematične metode za fizike. Obsežen vodnik. 7. izdaja. Akademski tisk. ISBN 978-0-12-384654-9
2. CC izračun. Rešeni cilindrični in sferični koordinatni problemi. Iztegnjeno od: izračun.DC
3. Astronomska delavnica. Širina in dolžina. Pridobljeno iz: stopnja.Blogspot.com/
4. Weisstein, Eric W. "Sferične koordinate.”S spleta MathWorld-A Wolfram. Okreval od: Mathworld.Wolfram.com
5. Wikipedija. Sferični koordinatni sistem. Pridobljeno iz: v.Wikipedija.com
6. Wikipedija. Vektorska polja v cilindričnih in sferičnih koordinatah. Pridobljeno iz: v.Wikipedija.com