Pravokotne koordinate primere in rešene vaje

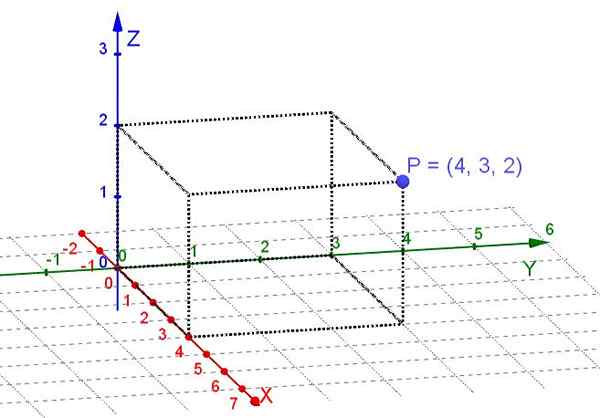
The Pravokotne koordinate O kartezijan so tisti, ki jih dobimo, ko jih projicirajo pravokotno na treh kartezijanskih osi x, y, z točko, ki se nahaja v tri -dimenzionalnem prostoru.

Kartezijanske osi so medsebojno pravokotno usmerjene naravnost. V kartezijanskem koordinatnem sistemu so v vsaki točki v prostoru dodeljene tri realne številke, ki so njegove pravokotne koordinate.

Slika 1. Pravokotne koordinate točke P (lastna izdelava)

Letala je podprostor v tridimenzionalnem prostoru. V primeru upoštevanja točk na ravnini je dovolj, da izberete par pravokotnih osi x in kot kartezijanski sistem. Potem sta na vsaki točki na ravnini dodeljeni dve resnični številki, da so njegove pravokotne koordinate.

[TOC]

Izvor pravokotnih koordinat

Pravokotne koordinate je prvotno predlagal francoski matematik René Descartes (1596 in 1650), zato prejmejo poimenovanje kartezijanov.

S to idejo o Descartesu se točke ravnine in prostora dodelijo številke, tako da so geometrijske številke povezale algebrsko enačbo in klasične geometrijske teoreme lahko prikazamo algebraično. S kartezijanskimi koordinatami se je rodila analitična geometrija.

Kartezijansko letalo

Če sta na ravnini izbrani dve pravokotni črti, ki se sekajo v eni točki ali; in če je tudi vsaki vrstici dodeljena smer in številčna lestvica med zaporednimi enakostalnimi točkami, je potem kartezijanski sistem ali načrt, v katerem je vsaka točka ravnine povezana z urejenim parom dveh resničnih številk, ki sta njeni projekciji na tem osi x in y.

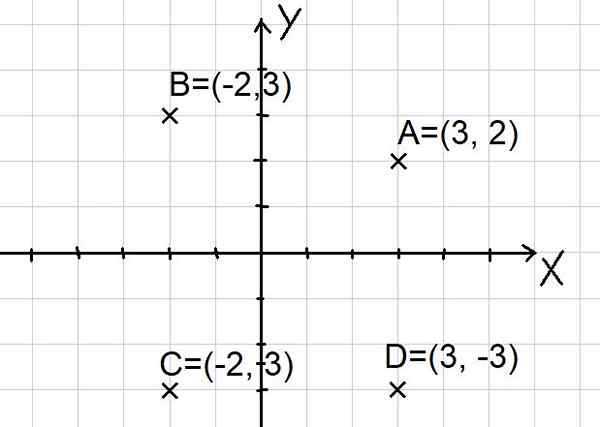
Točke a = (3, 2); B = (-2, 3); C = (-2, -3) in d = (3, -3) sta predstavljena v kartezijanski ravnini, kot je prikazano spodaj:

Slika 2. Točke na kartezijanski ravnini. (Lastna izdelava)

Upoštevajte, da dve osi x in y razdelita ravnino na štiri sektorje, imenovane kvadrante. Točka A je v prvem kvadrantu, B v drugem kvadrantu, C v tretjem kvadrantu in točki D v četrtem kvadrantu.

Vam lahko služi: populacija in vzorec

Razdalja med dvema točkama

Razdalja med dvema točkama A in B kartezijanske ravnine je dolžina segmenta, ki jih združuje. To razdaljo lahko izračunamo analitično na naslednji način:

D (a, b) = √ (bx - ax)^2 + (by - ay)^2)

Sprednja formula dobimo z uporabo teorema o pitagorah.

Uporaba omenjene formule na točkah A, B slike 2 je:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

To pomeni, da je D (a, b) = 5,10 enot. Upoštevajte, da je bila razdalja pridobljena brez potrebe po merjenju s pravilom, upoštevani je popolnoma algebrski postopek.

Analitični izraz črte

Pravokotne koordinate omogočajo analitični prikaz temeljnih geometrijskih predmetov, kot sta točka in črta. Dve točki A in B določita eno vrstico. Nagib črte je opredeljen kot količnik med razliko v koordinatah in točko B manj, deljeno z razliko v koordinatah x točke B manj a: a:

čaka = (by - ay)/(bx - sekira)

Vsaka točka koordinat (x, y), ki spada v črto (AB), mora imeti enak naklon:

čakajoča = (y - ay)/(x - sekira)

Enačba, ki jo dobimo z enakostjo pobočij, je analitična ali algebrska reprezentacija črte, ki poteka skozi točke A in B:

(y - ay)/(x - ax) = (by - ay)/(bx - sekira).

Če vas jemljete za A in B, so pravokotne koordinate slike 2:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

V tem konkretnem primeru obstaja črta z negativnim naklonom -⅕, kar pomeni, da se nahaja na točki črte in poveča koordinato x v enoti, koordinat in zmanjšuje v 0,2 enotah. 

Vam lahko služi: Toroid ali Toro Dona

Najbolj običajni način za pisanje enačbe vrstice v ravnini je s koordinato in jasno kot funkcija spremenljivke x:

y = -(1/5) x + 13/5 

Primeri

Primer 1

Pridobite z analitičnimi metodami razdaljo med točkami C in A, ki so pravokotne koordinate C = (-2, -3) in tistih A = (3.2).

Formula evklidske razdalje med tema dvema točkama je napisana tako:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Zamenjava ustreznih pravokotnih koordinat imate:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7.07

Primer 2

Pridobite enačbo črte, ki poteka skozi točko C koordinat (-2, -3) in točko P koordinate (2, 0).

Najprej dobimo naklon linije CP:

čakajoča = (0 -(-3)) / (2 -( -2)) = ¾ 

Vsaka točka Q generičnih pravokotnih koordinat (x, y), ki spada v linijo CP, mora imeti enak naklon:

čakajoča = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

To pomeni, da je enačba linije CP:

(Y +3) / (x +2) = ¾

Alternativni način za pisanje enačbe linije CP je čiščenje in:

y = ¾ x - 3/2 

Rešene vaje

Vaja 1

Pridobite pravokotne koordinate presečišča med črtami y = - (1/5) x + 13/5 in črto y = ¾ x - 3/2.

Rešitev: Po definiciji ima presečišče obeh vrstic enake pravokotne koordinate. Zato so koordinate in na mestu presečišča enaki za obe vrstici:

-(1/5) x + 13/5 = ¾ x - 3/2

Kaj vodi do naslednjega izraza:

Lahko vam služi: Laptoid Trapezoid: Lastnosti, odnosi in formule, primeri

(¾ + ⅕) x = 13/5 +3/2

Reševanje vsote frakcij se dobi:

19/20 x = 41/10

Kliranje x:

x = 82/19 = 4,32

Za pridobitev vrednosti in presečišča se vrednost x, dobljena v eni od črt, zamenja:

y = ¾ 4,32 - 3/2 = 1,74

To pomeni, da so dane črte prestrežene v točki I koordinat i = (4.32; 1,74).

Vaja 2

Pridobite enačbo oboda, ki poteka skozi pravokotno koordinatno točko R (3, 4) in ima središče pri izvoru koordinat.

Rešitev: Radio R je razdalja od točke R do izvora ali koordinat (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 2 + 4^2) = √ (9 + 16) = √ (25) = 5

Se pravi, da je polmer 5 krog 5 osredotočen na (0,0).

Vsaka točka P (x, y) oboda mora imeti enako razdaljo 5 do središča (0, 0) za tisto, kar je mogoče zapisati:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

To pomeni:

√ (x^2 + y^2) = 5

Za odpravo kvadratnega korena oba člana enakosti ostaneta tiho:

x^2 + y^2 = 25

Kaj je enačba oboda.

S tem primerom je prikazana moč pravokotnega koordinatnega sistema, ki omogoča določanje geometrijskih predmetov, kot je obod, brez potrebe po uporabi papirja, svinčnika in kompasa. Določen je obod, ki ga zahtevajo le algebrske metode.

Reference

1. Arfken g in weber h. (2012). Matematične metode za fizike. Obsežen vodnik. 7. izdaja. Akademski tisk. ISBN 978-0-12-384654-9
2. CC izračun. Pravokotne koordinate rešene težave. Iztegnjeno od: izračun.DC
3. Weisstein, Eric W. "Kartezijanske koordinate.”S spleta MathWorld-A Wolfram. Okreval od: Mathworld.Wolfram.com
4. Wikipedija. Kartezijanski koordinatni sistem. Pridobljeno iz: v.Wikipedija.com