Boltzmannova stalna zgodovina, enačbe, izračun, vaje

The Boltzmannova konstanta To je vrednost, ki navaja povprečno kinetično energijo termodinamičnega sistema ali objekta z absolutno temperaturo iste. Čeprav so pogosto zmedeni, temperatura in energija nista isti koncept.

Temperatura je merilo energije, ne pa tudi same energije. S konstanto Boltzmanna je eden med seboj povezan:

In_c = (3/2) k_B  T

Boltzmann gostitelj na Dunaju. Vir: Dadotet pri angleški Wikipediji [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Ta enačba velja za idealno molekulo monoatomske plina m, kje In_c To je njegova kinetična energija, dana v Joulesu, K_B To je Boltzmannova stalnica in T To je absolutna temperatura v Kelvinu.

Na ta način, ko se temperatura zvišuje, se poveča tudi povprečna kinetična energija po molekuli snovi, kot se pričakuje. In nasprotno se zgodi, ko se temperatura zniža in doseže točko, ko preneha celotno gibanje, dosežemo najnižjo možno ali absolutno temperaturo.

Ko govorimo o povprečni kinetični energiji, si je treba zapomniti, da je kinetična energija povezana z gibanjem. In delci se lahko premikajo na več načinov, na primer premikanje, vrtenje ali vibriranje. Seveda ne bodo vsi to storili na enak način, in ker so nešteto, potem se povprečje sprejme za karakterizacijo sistema.

Nekatere energetske države so bolj verjetno kot druge. Ta koncept je v termodinamiki radikalnega pomena. Energija, upoštevana v prejšnji enačbi, je kinetična energija prevajanja. Verjetnosti držav in njihovega odnosa z Boltzmannovo konstanto se bo pogovorilo malo kasneje.

Leta 2018 je bil Kelvin na novo definiran in z njim Boltzmannova konstanta, ki je v mednarodnem sistemu približno 1.380649 x 10^-23 J. K^-1. Za Boltzmannovo konstanto je mogoče doseči veliko več natančnosti, ki je bila določena v številnih laboratorijih po svetu, z različnimi metodami.

[TOC]

Zgodovina

Znana konstanta je svoje ime dolžna fiziku Ludwigu Boltzmannu (1844-1906), rojenem na Dunaju, ki je svoje življenje posvetil znanstveniku študiju statističnega vedenja sistemov s številnimi delci, z vidika newtonske mehanike.

Čeprav je danes obstoj atoma splošno sprejet, v devetnajstem stoletju prepričanje o tem, ali je atom res obstajal ali je bila umetnost, s katero je bilo razloženo veliko fizičnih pojavov.

Vam lahko služi: običajni vektor: izračun in primer

Boltzmann je bil močan branilec obstoja atoma in v svojem času se je soočal z ostrimi kritikami njegovega dela mnogih kolegov, ki so menili, da vsebujejo netopne paradokse.

Izjavil je, da je mogoče opaziti pojave na makroskopskih ravneh s statističnimi lastnostmi sestavnih delcev, kot so atomi in molekule.

Ta kritika je lahko posledica globoke epizode depresije, ki ga je pripeljala do svojega življenja v začetku septembra 1906, ko je imel še veliko opraviti, saj je veljal za enega izmed velikih teoretičnih fizikov svojega časa in tam in tam je bilo malo za to, da bodo drugi znanstveniki prispevali k potrditvi verodostojnosti svojih teorij.

Ni se zgodilo dolgo po njegovi smrti, ko bodo dodana nova odkritja o naravi atoma in njegovih sestavnih delcev, da bi dali razlog Boltzmannu.

Boltzmannova stalnica in Planckova dela

Zdaj pa Boltzmannova stalnica k_B Uveden je bil, kot je znano danes nekaj časa po delu avstrijskega fizika. Max Planck je bil v svojem zakonu emisije črnega telesa, ki ga je predstavil leta 1901, ki mu je takrat dal vrednost 1,34 x 10²³ J/k.

Do leta 1933 je bil Boltzmann na Dunaj dodan kot plakat, ki je dal plaketo z definicijo entropije, ki vključuje znamenito konstanto: S = k_B dnevnik w, enačba, o kateri bomo razpravljali kasneje.

Danes je Boltzmannova konstanta nepogrešljiva pri uporabi termodinamičnih zakonov, statističnih mehanikov in teorije informacij, na katerih je bil ta fizik s žalostnim koncem pionir.

Vrednost in enačbe

Pline lahko opišemo v makroskopskem smislu in tudi v mikroskopskem smislu. Za prvi opis obstajajo koncepti, kot so gostota, temperatura in tlak.

Vendar je treba spomniti, da je plin sestavljen iz številnih delcev, ki imajo globalno nagnjenost k določenemu vedenju. To je tisti trend, ki je makroskopsko meri. Eden od načinov za določitev Boltzmannove konstante je zahvaljujoč dobro znani enačbi idealnih plinov:

str.V = n. R. T

Tukaj str Je tlak plina, V To je njegova glasnost, n Je število prisotnih molov, R To je konstanta plinov in T To je temperatura. V molu idealnega plina je izpolnjen naslednji odnos med izdelkom str.V, in kinetično energijo prevajanja K Celoten niz je:

Vam lahko služi: korpuskularni model snovi

str.V = (2/3). K

Zato je kinetična energija:

K = (3/2) n.R.T

Z delitvijo s skupnim številom prisotnih molekul, ki se imenujemo N, dobimo povprečno kinetično energijo enega samega delca:

In_c = K /N

In_c= (3/2n) n.R.T

V mol je število delcev n_Do, In zato je skupno število delcev N = nnA, bivanje:

In_c = (3/2nn_Do) n.R.T

Natančno količnik R/n_Do Boltzmannova konstanta je dokazana, da je kinetična energija povprečnega prevajanja delca odvisna le od absolutne temperature in ne drugih velikosti, kot so tlak, volumen ali celo vrsta molekule:

In_c = (3/2) k_B. T

Boltzmannova stalnica in entropija

Plin ima določeno temperaturo, vendar lahko temperatura ustreza različnim stanjem notranje energije. Kako vizualizirati to razliko?

Razmislite o sočasnem zagonu 4 kovancev in načinov, kako lahko padejo:

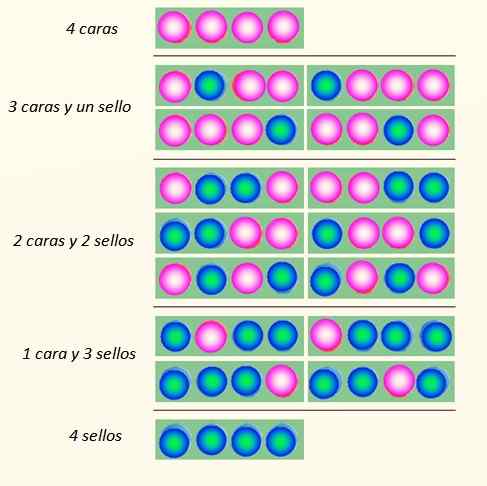Načine, kako lahko padejo 4 kovanci. Vir: Self Made

Kovček lahko prevzame skupno 5 držav, ki se upoštevajo Makroskopski, opisano na sliki. Katera od teh držav bi bralec rekel, da je najverjetneje?

Odgovor naj bo stanje dveh obrazov in 2 križa, ker ima skupno 6 možnosti, od 16 prikazanih na sliki. In 2⁴ = 16. Te so enakovredne državam mikroskopski.

In kaj, če se namesto 4 zažene 20 kovancev? Bila bi skupno 2^dvajset možnosti ali "mikroskopska stanja". Je veliko večje in težje število. Za lažje upravljanje velikih številk so logaritmi zelo primerni.

Zdaj se zdi očitno, da je država z največjo motnjo najverjetnejša. Najbolj urejene države, kot so 4 obrazi ali 4 znamke.

Entropija makroskopskega stanja je opredeljena kot:

S = k_B ln w

Kje W Je število možnih mikroskopskih stanj in k_B To je Boltzmannova konstanta. Kot ln w Je brezdimenzionalna, entropija ima enake enote kot k_B: Joule/k.

To je znana enačba v Boltzmannovem nagrobniku na Dunaju. Vendar je več kot entropija pomembna sprememba:

Lahko vam služi: termodinamične spremenljivke: katere so in rešene vaje

ΔS = k_B ln w₂ - k_B ln w₁ = k_B ln (w₂/w₁)

Kako se izračuna K_B?

Vrednost Boltzmannove konstante dobimo eksperimentalno natančno z meritvami, ki temeljijo na Akustična termometrija, ki se izvajajo s pomočjo lastnosti, ki vzpostavlja odvisnost od hitrosti zvoka v plinu s temperaturo iste.

Dejansko je hitrost zvoka v plinu dana:

Kjer b _adiabatski To je modul adiabatske stisljivosti, ki ga daje:

B_adiabatski = γP

In ρ je gostota plina. Za prejšnjo enačbo, str Je pritisk zadevnega plina in γ To je adiabatski koeficient, katerega vrednost za določen plin najdemo v tabelah.

Metrološki inštituti doživljajo tudi druge načine merjenja konstante, na primer Johnson Noise Termometrija, ki uporablja toplotna nihanja, ki se pojavljajo naključno v materialih, zlasti pri voznikih.

Rešene vaje

-Vaja 1

Najti:

a) Kinetična energija povprečnega prevoda In_c ki ima idealno molekulo plina pri 25 ° C

b) kinetična energija prevajanja K molekul v 1 mol tega plina

c) Povprečna hitrost molekule kisika pri 25 ° C

Dejstvo

m_kisik = 16 x 10 ^-3 kg/mol

Rešitev

na) In_c = (3/2) k t = 1.5 x 1.380649 x 10^-23J. K^-1 x 298 k = 6.2 x 10^{-enaindvajset} J

B K = (3/2) n.R.T = 5 x 1 mol x 8.314 j/mol .K x 298 k = 3716 J

c) In_c = ½ mV², Ob upoštevanju, da je molekula kisika diatomska, molarna masa pa je treba pomnožiti z 2, bo:

-Vaja 2

Poiščite spremembo entropije, ko je 1 mol plina zasedeno z volumnom 0.5m³ Razširi se na zasedbo 1 m³.

Rešitev

ΔS = k_B ln (w₂/w₁)

W₂= 2^NW₁ (Bila sta 2⁴ Mikroskopska stanja za začetek štirih kovancev, ne pozabite?)

Kjer je n število delcev, ki so prisotni v 0.5 mol plina 0.5 x n_Do:

ΔS = k_B ln (2^N W₁/w₁) = k_B ln 2^N= k_B 0.5n_Do ln 2 = 2.88 j/k

Reference

1. Atkins, str. 1999. Fizikalna kemija. Omega izdaje. 13-47.
2. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 664-672.
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. ... Ed Prentice Hall. 443 -444.
4. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. 647-673.
5. Če redefinicija. Kelvin: Boltzmann Constant. Okreval od: NIST.Gov