Radialna obremenitev Kako se izračuna, rešene vaje

The Radialna obremenitev To je sila, ki se pravokotno izvaja na os simetrije predmeta in katere linija delovanja gre skozi to osi. Na primer, pas na škripcu nalaga radialno obremenitev ležaja ali ležaja osi istega.

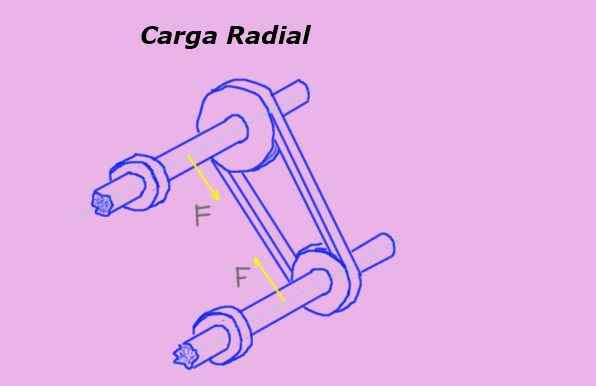
Na sliki 1 rumene puščice predstavljajo radialne sile na osi zaradi napetosti jermena, ki poteka skozi škripce.

Slika 1. Radialna obremenitev na osi škripcev. Vir: Self Made.

Enota merjenja radialne obremenitve v mednarodnem sistemu ali če je Newton (n). Toda za merjenje so uporabljene tudi druge enote sile, kot sta kilogramska sila (kg-f) in trdnost funta (LB-F).

[TOC]

Kako se izračuna? 

Za izračun vrednosti radialne obremenitve v elementih strukture je treba upoštevati naslednje korake:

- Naredite diagram sil na vsakem elementu.

- Uporabite enačbe, ki zagotavljajo translacijsko bilanco; to pomeni, da je vsota vseh sil nična.

- Razmislite o enačbi navorov ali trenutkov, tako da je rotacijsko ravnovesje izpolniti. V tem primeru mora biti vsota vseh navora nična.

- Izračunajte sile, da prepoznajo radialne obremenitve, ki delujejo v vsakem od elementov.

Rešene vaje

-Vaja 1

Naslednja slika prikazuje jermenica, skozi katero prehaja napev jermenica z napetostjo t. Jermenica je nameščena na osi, ki počiva na dveh chumacerah. Središče enega od njih je na daljavo l₁ iz središča jermenice. Na drugem koncu je druga chumacera, na daljavo l₂.

Lahko vam služi: Higroskopičnost: koncept, higroskopske snovi, primeri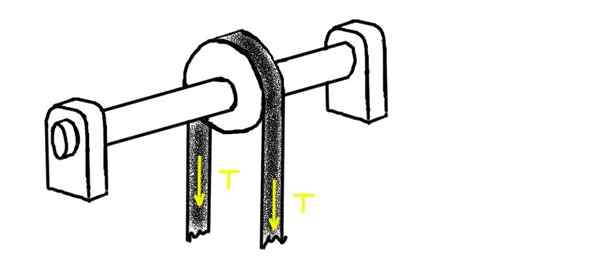Slika 2. Jermenica, skozi katero prehaja napet jermen. Vir: Self Made.

Določite radialno obremenitev vsakega od chumaceras, ob predpostavki, da sta teža osi in jermenice precej nižja od uporabe napetosti.

Vzemite kot vrednost za 100 kg-f pasu in za razdalje L₁= 1 m in l₂= 2 m.

Rešitev

V prvi vrsti je narejen diagram sil, ki delujejo na osi.

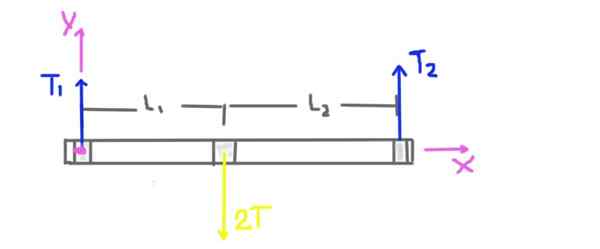Slika 3. Diagram sil vadbe 1.

Napetost škripec je t, vendar je radialna obremenitev na osi v položaju jermenice 2t. Teža osi in jermenice se ne upošteva, ker nam izjava o težavah pove, da je veliko nižja od napetosti, ki se uporablja za pas.

Radialna reakcija nosilcev povzročata radialne sile ali obremenitve T1 in T2. Razdalja L1 in L2 nosilcev v središču škripca sta tudi prikazani na diagramu.

Prikazan je tudi koordinatni sistem. Navor ali skupni trenutek na osi se izračuna kot središče izvor koordinatnega sistema in bo pozitiven v smeri z.

Ravnotežni pogoji

Zdaj so vzpostavljeni ravnotežni pogoji: vsota iste nič in vsota navora enaka ničla.

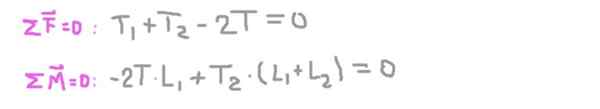
Iz druge enačbe radialna reakcija na osi na podpori 2 (t₂), zamenjava v prvi in ​​čiščenje radialne reakcije na osi v podpori 1 (t₁).

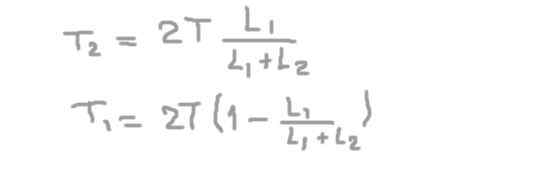Če nadomestimo številčne podatke, dobimo, da je radialna obremenitev ali sila na osi v položaju podpore 1:

T₁= (2/3) t = 66,6 kg-f

Lahko vam služi: kalibracijska krivulja: za kaj je, kako to storiti, primeri

In radialna obremenitev osi v podpori podpore 2 je:

T₂= (4/3) t = 133,3 kg-f.

Vaja 2

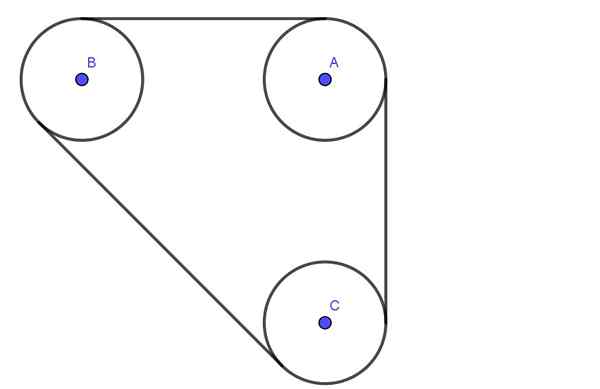
Naslednja slika prikazuje sistem, sestavljen iz treh jermenic A, B, C vse radio r. Jermenice so povezane s pasom, ki ima napetost T.

Osi a, b, c prehodi mazane ležaje. Ločitev med središči osi A in B je 4 -krat večja od polmera r. Podobno je tudi ločitev med osi B in C 4R.

Določite radialno obremenitev osi škripcev A in B, ob predpostavki, da je napetost pasu 600n.

Slika 4. Sistem jermenic. Vaja 2. (Lastna izdelava)

Rešitev

Začne se z risanjem diagrama sil, ki delujejo na škripec A in B. Pri prvem imate obe napetosti₁ in t₂, kot tudi sila f_Do Da ležaj izvaja na osm jermenice.

Podobno na jermenici B imate napetosti t₃ , T₄ in sila f_B da ležaj izvaja na osi istega. Radialna obremenitev na osi škripca A je sila F_Do In radialna obremenitev na B je sila F_B.

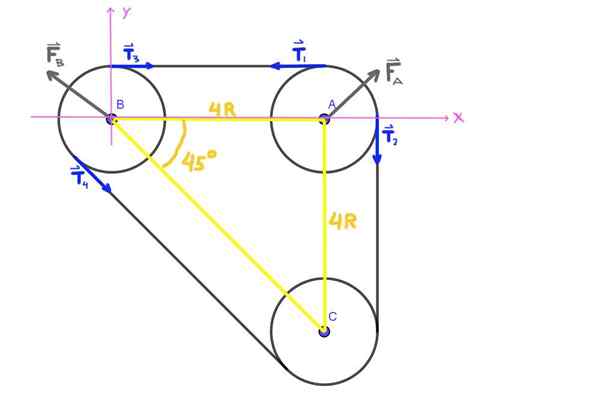Slika 5. Shema sil, vaja 2. (Lastna izdelava)

Ko seki.

Vse napetosti t₁ , T₂ , T₃ , T₄ Prikazan na sliki ima isti modul T, ki je napetost jermena.

Stanje ravnotežja za jermenico a

Zdaj zapišemo stanje ravnotežja za jermenico, na katerega ni nič drugega kot vsota vsega sile, ki delujejo na jermenici A, mora biti nična.

Ločitev komponent x in y od sil in dodajanje (vektorično) je dosežen naslednji par skalarnih enačb:

Vam lahko služi: Titan (satelit)

F_DoX - T = 0; F_DoIn - T = 0

Te enačbe vodijo do naslednje enakosti: F_Sekira = F_Oh = T.

Zato ima radialna obremenitev velikosti:

F_Do = (T² + t²)^1/2 = 2^1/2∙ t = 1,41 ∙ t = 848,5 N. 45 ° smer. 

Stanje ravnotežja za jermenica B

Podobno napišemo ravnotežni pogoj za škripec B. Za komponento x imate: f_BX + T + t ∙ cos45 ° = 0

In za komponento y: f_BIn + T ∙ Sen45 ° = 0

Tako:

F_Bx = - t (1+2^-1/2) in f_Mimo = -T ∙ 2^-1/2

To pomeni, da je velikost radialne obremenitve na škripcu B:

F_B = ((1+2^-1/2) ² + 2^-1)^1/2∙ t = 1,85 ∙ t = 1108,66 n in njegov naslov je 135 °.

Reference

1. Beer F, Johnston E, Dewolf J, Mazurek, D. Mehanika materialov. Peta izdaja. 2010. MC Graw Hill. 1-130.
2. Gere J, Goodno, B. Mehanika materialov. Osma izdaja. Cengage učenje. 4-220.
3. Giancoli, d. 2006. Fizika: načela z aplikacijami. 6^Tth Ed. Dvorana Prentice. 238-242.
4. Hibbeler R. Mehanika materialov. Osma izdaja. Dvorana Prentice. 2011. 3-60.
5. Valera Negrete, J. 2005. Splošne zapise o fiziki. Ne. 87-98.