Antiderivacijske formule in enačbe, primeri, vaje

A Antiderivacijsko F (x) funkcije F(x) se imenuje tudi primitiven ali preprosto nedoločen integral omenjene funkcije, če je v določenem intervalu Yo, Res je, da F '(x) = f (x)

Na primer, vzemimo naslednjo funkcijo:

f (x) = 4x³

Antiderivacija te funkcije je f (x) = x⁴, Ker z izpeljavo f (x) s pravilom izpeljave za pooblastila:

Dobimo natančno f (x) = 4x³.

Vendar je to le eden izmed številnih antiderivativov F (x), saj ta druga funkcija: g (x) = x⁴ + 2 To je tudi, ker z izpeljavo g (x) glede na x je enako, dobimo nazaj f (x).

Preverimo:

Ne pozabite, da je tisti, ki izhaja iz konstante, 0. Torej na izraz x⁴ Lahko dodate katero koli konstanto in njegov izpeljan bo še naprej 4x³.

Sklenjeno, da je vsaka funkcija splošne oblike f (x) = x⁴ + C, kjer je C resnična konstanta, služi kot antiderivacija F (x).

Prejšnji ilustrativni primer je mogoče izraziti na naslednji način:

df (x) = 4x³ Dx

Nedefinirani antiderivacijski ali integral je izražen s simbolom ∫, torej:

F (x) = ∫4x³ dx = x⁴ + C

Kjer je funkcija f (x) = 4x³  Se imenuje integracija, in C je Konstanta integracije.

[TOC]

Primeri antiderivativov

Slika 1. Anti -hotley ni nič drugega kot nedoločen integral. Vir: Pixabay.

Iskanje antiderivacije funkcije je v nekaterih primerih preprosto, v katerih so derivati ​​dobro znani. Na primer, bodite funkcija f (x) = sen x, nerederivirana za to je druga funkcija f (x), tako da, ko jo dobimo f (x).

Ta funkcija je lahko:

F (x) = - cos x

Preverimo, da je res:

F '(x) = (- cos x)' =- (-sen x) = sin x

Zato lahko pišemo:

∫sen x dx = -cos x + c

Poleg poznavanja derivatov obstajajo osnovna in preprosta pravila integracije za iskanje nedoločenega antiderivacijskega ali integralnega dela.

Vam lahko služi: zaporedni derivati

Biti resnična konstanta, potem pa:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Če lahko funkcijo H (x) izrazimo kot vsota ali odštevanje dveh funkcij, potem je njegov nedoločen integral:

3.- ∫H (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

To je lastnost linearnosti.

The Pravilo moči Za integrale je mogoče določiti na ta način:

To pravilo ima očitno omejitev: od imenovalca N +1 Ni mogoče storiti 0, torej n ≠ -1.

V primeru n = -1 se uporablja naslednje pravilo:

5.- ∫x ^-1 Dx = ln x +c

Enostavno je dokazati, da je derivat ln x Točno je x ^-1.

Diferencialne enačbe

Diferencialna enačba je tista, v kateri je neznano kot derivat.

Zdaj je iz prejšnje analize enostavno spoznati, da je obratno delovanje derivata nedefinirano antiderivativno ali integral.

Naj bo f (x) = y '(x), torej izhaja iz določene funkcije. Za označevanje tega izpeljave lahko uporabimo naslednji zapis:

Takoj sledi, da:

dy = f (x) dx

Neznano o diferencialni enačbi je funkcija y (x), tista, katere derivat je f (x). Da bi ga razčistili, je prejšnji izraz integriran na obeh straneh, kar je enakovredno uporabi antiderivacij:

∫dy = ∫f (x) dx

Levi integral je razrešen s pravilom integracije 1 s k = 1 in s tem je iskana -awaite očiščena:

in (x) = ∫f (x) dx = f (x) + c

In ker je C resnična konstanta, če želite vedeti, katera je primerna v vsakem primeru, mora izjava vsebovati dovolj dodatnih informacij za izračun vrednosti C. To se imenuje Začetni pogoj.

Primeri vse to bomo videli v naslednjem razdelku.

Vam lahko služi: natančna ocena

Antiderivirane vaje

- Vaja 1

Uporabite pravila integracije, da pridobite naslednje nedefinirane antiderivative ali integrale danih funkcij in čim bolj poenostavite rezultate. Rezultat je priročno z izpeljavo.

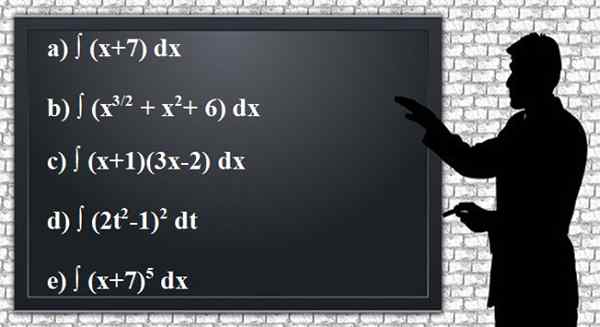Slika 2. Definirane prednje ali integralne vaje. Vir: Pixabay.

Rešitev

Najprej uporabimo pravilo 3, saj je integracija vsota dveh izrazov:

∫ (x +7) dx = ∫ xdx +∫7dx

Za prvi integral se uporablja pravilo pooblastil:

∫ xdx = (x² /2)+c₁

V drugem integralnem pravilu 1 velja K = 7:

∫7dx = 7∫dx = 7x + c₂

In zdaj so dodani rezultati. Obe konstanti sta združeni v eno, splošno imenovani C:

∫ (x+7) dx = (x² /2) + 7x + c

Rešitev b

Z linearnostjo se ta integral razkroji v tri preprostejše integrale, za katere se bo uporabljalo pravilo pooblastil:

∫ (x^3/2 + x² + 6) dx = ∫x^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Upoštevajte, da se za vsak integral pojavi konstanta integracije, vendar se srečajo v enem klicu C.

Rešitev c

V tem primeru je priročno uporabiti distribucijsko lastnost množenja za razvoj integracije. Nato uporabite pravilo pooblastil za iskanje vsakega integrala ločeno, kot v prejšnjem letu.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) dx

Pozorni bralec bo opazil, da sta dva osrednja izraza podobna, zato sta se pred integracijo zmanjšala:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Rešitev e

Način za reševanje integrala bi bil razvoj moči, kot je bilo to storjeno v primeru D. Ker pa je eksponent višji, bi bilo treba spremeniti spremenljivo spremembo, da ne bi bilo treba tako dolgo.

Vam lahko služi: neprekinjena naključna spremenljivka

Spremenljiva sprememba je naslednja:

U = x + 7

Izpeljava na obeh straneh tega izraza:

du = dx

Integral se pretvori v enostavnejšo z novo spremenljivko, ki je razrešena s pravilom moči:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Končno se sprememba vrne, da se vrne v prvotno spremenljivko:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Vaja 2

Delec je sprva v mirovanju in se premika vzdolž osi x. Njegov pospešek za T> 0 je podan s funkcijo a (t) = cos t. Znano je, da je pri t = 0 položaj x = 3, vse v enotah mednarodnega sistema. Zahteva se, da najdete hitrost V (t) in položaj x (t) delca.

Rešitev

Ker je pospešek prvi izpeljan iz hitrosti glede na čas, imate naslednjo diferencialno enačbo:

a (t) = v '(t) = cos t

Sledi, da:

v (t) = ∫ cos t dt = sin t + c₁

Po drugi strani pa vemo, da je hitrost izpeljana položaja, zato se spet integriramo:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

Konstante integracije so določene iz informacij, navedenih v izjavi. Najprej pravi, da je bil delček sprva v mirovanju, torej V (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Potem morate x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + c₂ = 3 → C₂ = 3+1 = 4

Funkcije hitrosti in položaja so vsekakor takšne:

v (t) = sen t

x (t) = - cos t + 4

Reference

1. Engler, a. 2019. Integralni računanje. Nacionalna univerza na obali.
2. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
3. Brezplačna besedila matematike. Antiderivativi. Okrevano od: matematika.LiibreTexts.org.
4. Wikipedija. Antiderivacijsko. Pridobljeno iz: v.Wikipedija.org.
5. Wikipedija. Nedočasna integracija. Okrevano od: je.Wikipedija.org.