Karakteristike amplitude valov, formule in vadbe

The Amplituda valov To je največji premik, ki ga doživlja točka v valu glede na ravnotežni položaj. Valovi se manifestirajo povsod in na veliko načinov na svetu okoli nas: v oceanu, v zvoku in v vrvi instrumenta, ki ga proizvaja, v svetlobi, na zemeljski površini in še veliko več.

Eden od načinov za izdelavo valov in preučevanje njenega vedenja je opazovanje vibracije vrvi, ki ima fiksni konec. Z motnjo na drugem koncu se vsak delček vrvi niha in z njo se energija motnje prenaša v obliki zaporedja impulzov po vsem.

Valovi se v naravi manifestirajo na več načinov. Vir: Pixabay.

Ko se energija širi, vrv, ki naj bi bila popolnoma elastična, sprejme tipično sinusoidno obliko z grebeni in dolinami, prikazanimi na sliki, ki se prikaže spodaj v naslednjem razdelku.

[TOC]

Značilnosti in pomen amplitude valov

Amplituda A je razdalja med grebenom in referenčno osi ali stopnjo 0. Če je prednostno, med dolino in referenčno osi. Če je motnja v vrvi blag, je amplituda A majhna. Če je nasprotno motnje intenzivna, bo amplituda večja.

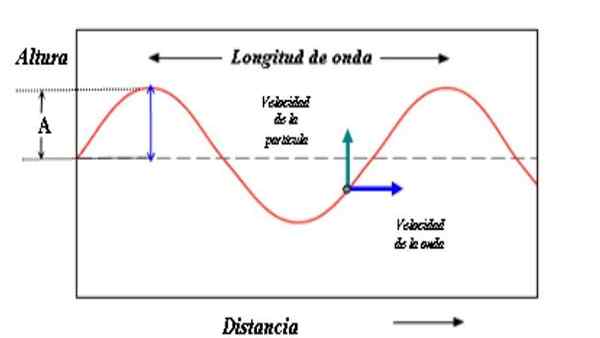Model za opis vala je sestavljen iz sinusoidne krivulje. Amplituda valov je razdalja med grebenom ali dolino in referenčno osi. Vir: PACO [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Vrednost amplitude je tudi merilo energije, ki nosi val. Intuitivno je, da je velika amplituda povezana z večjimi energijami.

Dejansko je energija sorazmerna s kvadratom amplitude, ki je matematično izrazila:

I ∝a²

Vam lahko služi: medsebojna induktivnost: formula/koeficient, aplikacije, vaje

Kjer sem intenzivnost vala, je povezana z energijo.

Vrsta vala, ki nastane v primeru vrvi, spada v kategorijo mehanskih valov. Pomembna značilnost je, da vsak delček na vrvi vedno ostane zelo blizu njegovega ravnotežnega položaja.

Delci se ne premikajo in ne premikajo skozi vrv. Segajo navzgor in navzdol. To je prikazano v zgornji shemi z zeleno puščico, vendar val skupaj z energijo potuje od leve proti desni (Modra puščica).

Valovi, ki se širijo v vodi, zagotavljajo potrebne dokaze, da se prepričajo o tem. Opazovanje gibanja lista, ki je padel v ribnik, je razvidno, da preprosto niha, ki spremlja gibanje vode. Vsaj jasno ne gre zelo daleč, da obstajajo druge sile, ki zagotavljajo druge gibe.

Valovni model, prikazan na sliki, je sestavljen iz ponavljajočega se vzorca, v katerem je razdalja med dvema grebenama valovna dolžina λ. Če želite, valovna dolžina loči tudi dve enaki točki od vala, tudi ko nista na grebenu.

Matematični opis vala

Seveda lahko val opišemo z matematično funkcijo. Periodične funkcije, kot sta sinus in kosinus, so idealne za nalogo, ne glede na.

Če na sliki pokličemo navpično osi in vodoravno osi, ki jo imenujemo "t", potem se vedenje vala skozi čas izraža z:

y = a cos (ωt + δ)

Za to idealno gibanje vsak delček vrvi niha s preprostim harmoničnim gibanjem, kar izvira zaradi sile, ki je neposredno sorazmerna z premikom, ki ga naredi delček.

Vam lahko služi: Dirac Jordan Atomski model: značilnosti in postulati

V predlagani enačbi so a, ω in Δ parametri, ki opisujejo gibanje, pri čemer so do amplituda prej opredeljen kot največji premik, ki ga je doživel delček glede na referenčno osi.

Argument kosinusa se imenuje Faza gibanja In Δ je fazna konstanta, Kakšna je faza, ko t = 0. Tako kosinusna funkcija in sinusna funkcija sta primerna za opis vala, saj se med seboj razlikujejo le π/2.

Za poenostavitev izraza je običajno mogoče izbrati t = 0 z Δ = 0 in pridobiti:

y = a cos (ωt)

Ko se gibanje ponavlja tako v prostoru kot v času, je značilen čas, ki je obdobje t, opredeljen kot čas, ki je potreben za delček, da izvede popolno nihanje.

Opis valov v času: značilni parametri

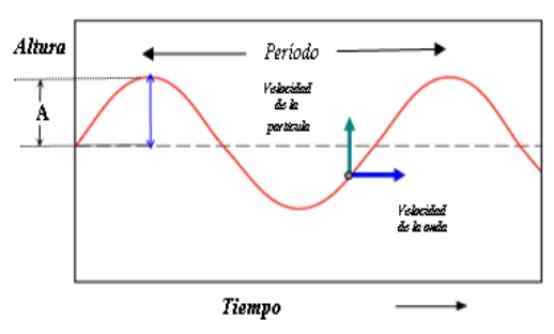Ta slika prikazuje opis vala v času. Razdalja med grebeni (ali dolinami) zdaj ustreza obdobju valov. Vir: PACO [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Zdaj tako dojka kot kosinus ponovita svojo vrednost, ko se faza poveča v vrednosti 2π, tako da:

ωt = 2π → ω = 2π /t

Ω se imenuje kotna frekvenca gibanja In ima dimenzije obratnega časa, saj so njene enote v mednarodnem sistemu Radián / Second ali Second^-1.

Končno lahko določite Frekvenca gibanja F, kot obratno ali vzajemno. Predstavlja v številu grebenov na enoto časa, v tem primeru:

F = 1/t

Ω = 2πf

Tako F kot ω imata enake dimenzije in enote. Poleg drugega^-1, ki se imenuje Hertz ali Hertzio, običajno je slišati Revolucije na sekundo tudi revolucije na minuto.

Valovna hitrost v, ki je treba poudariti, da ni isto kot tisti, ki ga doživljajo delci, ga je mogoče enostavno izračunati, če sta znana valovna dolžina λ in frekvenca f:

Lahko vam služi: svetlobna telesa: značilnosti in kako ustvarjajo svojo svetlobo

V = λf

Če je nihanje, ki ga doživljajo delci, preproste harmonične vrste, kotna frekvenca in frekvenca odvisna le od narave nihajnih delcev in značilnosti sistema. Amplituda vala ne vpliva na te parametre.

Na primer, pri igranju glasbene note na kitari bo nota vedno imela enak ton, čeprav se ga dotakne z večjo ali manjšo intenzivnostjo, na ta način bo vedno zvenel kot do skladba, bodisi na klavirju ali na kitari.

V naravi so valovi, ki se v materialnem okolju prevažajo v vse smeri, oslabljeni, ker se energija razprši. Zaradi tega se amplituda zmanjšuje z obratno razdaljo r vir, ki je mogoče potrditi:

A∝1/r

Vaja rešena

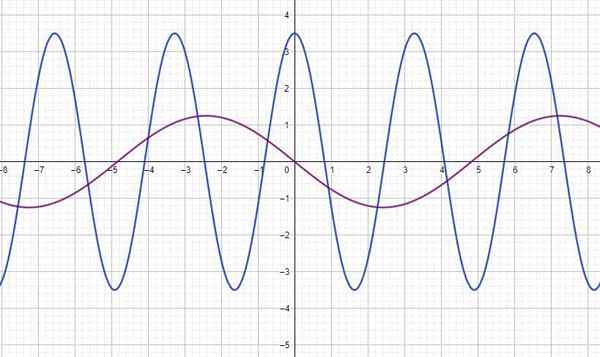
Slika prikazuje funkcijo y (t) za dva vala, kjer in je v metrih in t v nekaj sekundah. Za vsako najdbo:

a) amplituda

b) obdobje

c) frekvenca

d) enačba vsakega vala v smislu prsi ali cosens.

Odgovori

a) Meri se neposredno iz grafa s pomočjo omrežja: Blue Wave: A = 3.5m; Fuchsia val: a = 1.25 m

b) Prebere tudi graf in določi ločitev med dvema vrhoma ali dolinami, zaporedno: Modri ​​val: T = 3.3 sekunde; Fuchsia val t = 9.7 sekund

c) Izračuna se spomni, da je frekvenca vzajemna obdobja: Modri ​​val: F = 0.302 Hz; Fuchsia val: f = 0.103 Hz.

d) modri val: y (t) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Fuchsia val: y (t) = 1.25 greh (0.65T) = 1.25 cos (0.65T+1.57)

Upoštevajte, da je val Fuchsia zastarel π/2 glede na modro, kar ga je mogoče predstavljati s sinusovo funkcijo. Ali razseljen kosinus π/2.