Povprečni pospešek, kako izračunane in rešene vaje

The Povprečni pospešek do_m Velikost opisuje spreminjanje hitrosti delca v času. Pomembno je, ker kaže različice, ki jih gibanje doživlja.

Če želite izraziti to velikost v matematičnem smislu, je treba upoštevati dve hitrosti in dva trenutka časa, ki sta označena kot V₁ in v₂, in t₁ in t₂.

Povprečni pospešek je zelo pomemben filmski parameter. Vir: Pixabay.

Združevanje vrednosti v skladu s ponujeno definicijo bo sprejeti naslednji izraz:

V mednarodnem sistemu, če so enote za a_m bo m/s², Čeprav bodo druge enote, ki vključujejo dolžino na enoto časa na kvadratu.

Na primer je km/h.s To bere "kilometer na uro in za drugo". Upoštevajte, da se časovna enota pojavi dvakrat. Če razmišljate o mobilnem telefonu, ki se premika po ravni črti, to pomeni, da za vsako sekundo mobilni telefon poveča svojo hitrost za 1 km/h. Ali se za vsako sekundo zmanjša za 1 km/h, ki mineva.

[TOC]

Pospešek, hitrost in hitrost

Čeprav je povezan s pospeševanjem s povečanjem hitrosti, je resnica, da natančno opazujemo definicijo, se izkaže, da vsaka sprememba hitrosti pomeni obstoj pospeška.

In hitrost se ne spreminja vedno v velikosti. Se lahko zgodi, da se mobilni telefon le od smeri razlikuje in ohranja hitrost konstantne. Še vedno je za to spremembo odgovoren pospešek.

Primer tega je avtomobil, ki daje krivuljo s konstantno hitrostjo 60 km/h. Vozilo je podvrženo pospeševanju, ki je odgovoren za spremembo smeri hitrosti, tako da avtomobil sledi krivulji. Gonilnik ga uporablja z volanom.

Takšen pospešek je usmerjen proti središču ukrivljene poti, da avtomobil ne izstopi iz njega. Prejemajte ime pospeška radialno tudi normalno. Če je bil radialni pospešek nenadoma razveljavljen, avtomobil ni mogel več dati krivulje in nadaljevati v ravni črti.

Vam lahko služi: Wimshursst Machine: Zgodovina, kako deluje in aplikacije

Avto, ki se premika skozi krivuljo. V tem primeru je edini učinek pospeška sprememba hitrosti avtomobila.

Ta pospešek se imenuje pospešek tangencialna. Ni izključno za eno -dimenzionalno gibanje. Avto, ki daje krivuljo pri 60 km/h, lahko hkrati pospeši 70 km/h, medtem ko ga jemlje. V tem primeru mora voznik uporabiti tako volan kot pedal za plin.

Če upoštevamo eno -dimenzionalno gibanje, ima povprečni pospešek geometrijsko razlago, podobno kot povprečna hitrost, kot naklon sušilne črte, ki razreže krivuljo v točkah P in Q grafa hitrosti v primerjavi s časom.

To je razvidno na naslednji sliki:

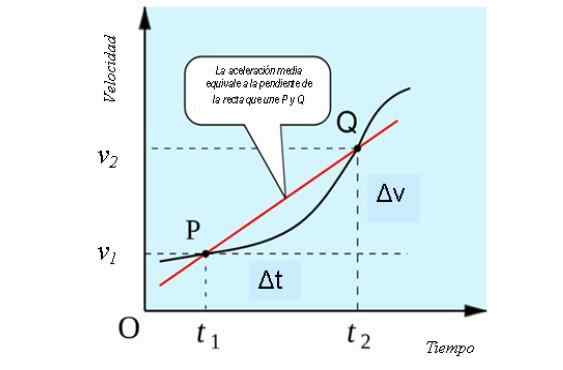Geometrijska razlaga povprečnega pospeška. Vir: Vir: すじにく シチュー [CC0].

Kako se izračuna povprečni pospešek

Poglejmo nekaj primerov za izračun povprečnega pospeška v različnih situacijah:

I) V določenem trenutku ima mobilni telefon, ki se premika po ravni črti, hitrost + 25 km/h, 120 sekund kasneje pa ima še en -10 km/h. Kakšen je bil povprečni pospešek?

Odgovor

Ker je gibanje eno -dimenzionalno, lahko vektorski zapis izpustimo, v tem primeru:

v_tudi = +25 km/h = +6.94 m/s

v_F = -10 km/h = - 2.78 m/s

ΔT = 120 s

Kadar koli imate vajo z mešanimi velikostmi, kot je ta, v katerih so ure in sekunde, je treba vse vrednosti prenesti na iste enote.

Ker je vektorsko zapisovanje, je bilo zapisano.

Ii) kolesar se premika proti vzhodu s hitrostjo 2.6 m/s in 5 minut kasneje gre proti jugu do 1.8 m/s. Poiščite njegov povprečni pospešek.

Lahko vam služi: Vy Canis Majoris: odkritje, značilnosti, struktura, usposabljanje in evolucija

Odgovor

Gibanje ni eno -dimenzionalno, zato se uporablja vektorska zapis. Vektorji enot Yo in J Navedejo naslove poleg naslednje konvencije o znakih, kar olajša izračun:

• Sever: +J
• Jug: -J
• To: +Yo
• Zahod: -Yo

v₂ = - 1.8 J gospa

v₁ = + 2.6 Yo gospa

ΔT = 5 minut = 300 sekund

Znaki pospeška v enem -dimenzionalnem gibanju

Kot vedno se zgodi s povprečnimi ali povprečnimi velikostmi, so posredovane informacije globalne. V vsakem trenutku ne ponujajo podrobnosti o tem, kaj se je zgodilo z mobilnikom, vendar to, kar prispevajo, ostaja dragoceno za opis gibanja.

Skozi oba znaka hitrosti in pospeševanja je mogoče vedeti, ali se mobilni telefon, ki se premika po liniji. V obeh situacijah je pospešek prisoten, saj se hitrost spreminja.

To je nekaj zanimivih pomislekov glede znakov teh dveh velikosti:

• Povprečna hitrost in pospeševanje, oba istega znaka, pomeni, da mobilni telefon postaja vse hitrejši in hitrejši.
• Hitrost in pospešek z različnimi znaki je znak, da se mobilni telefon podpisuje.

Običajno se misli, da kadarkoli gre za negativno pospeševanje, mobilni telefon zavira. To je res, če je mobilna hitrost pozitivna. Če pa je negativna, se v resnici hitrost povečuje.

Kot vedno, ko se gibanje preučuje, se razmišljajo o posebnih primerih. Na primer, kaj se zgodi, ko je povprečni pospešek nič?. Ali to pomeni, da je mobilni telefon vedno ohranjal svojo konstantno hitrost?

Odgovor je ne. Mobilni mobilni telefon bi lahko spremenil svojo hitrost v obravnavanem intervalu, vendar sta bila začetna hitrost in končna enaka. Trenutno podrobnosti o tem, kaj se je zgodilo v intervalu, niso znane, saj povprečni pospešek ne ponuja več informacij.

Vam lahko služi: Joule Effect: Pojasnilo, primeri, vaje, aplikacije

Kaj pa, če povprečni pospešek do_m Je enako pospeševanju do Na kateri koli točki začasnega intervala? To je zelo zanimiva situacija, imenovana pravokotno gibanje enakomerno raznoliko ali MRUV).

Pomeni, da se hitrost sčasoma enakomerno spreminja. Zato je pospešek konstanten. V naravi obstaja takšno gibanje, s katerim so vsi znani: svobodni padec.

Prosti padec: gibanje s stalnim pospeševanjem

Znano je dejstvo, da zemlja privabi predmete proti svojem.8 m/s² blizu površine.

Če zračna odpornost ne posreduje, je gibanje navpično in je znano kot prosti padec. Ko je pospešek konstanten in izbira t₀ = 0, povprečna enačba pospeška se spremeni v:

Kjer dobimo dobro znano formulo, da najdete hitrost v vsakem trenutku padca:

v_F = v₀ + At = gt (v₀= 0)

Kjer je a = g = 9.8 m/s²

Vaja rešena

Predmet se spusti z dovolj višine. Poiščite hitrost po 1.25 sekund.

Odgovor

v_tudi = 0, ker je predmet spuščen, potem:

v_F = Gt = 9.8 x 1.25 m/s = 12.25 m/s, usmerjeno navpično proti tla. (Vertikalna smer je bila odvzeta kot pozitivna).

Ko se objekt približuje tleh, se njegova hitrost poveča za 9.8 m/s za vsako pretečeno sekundo. Masa predmeta ni vključena. Dva različna predmeta, spuščena z iste višine in hkrati razvijeta enako hitrost, kot padeta.

Reference

1. Giancoli, d. Fizika. Načela z aplikacijami. Šesta izdaja. Dvorana Prentice. 21-35.
2. Resnick, r. (1999). Fizično. Zvezek 1. Tretja izdaja v španščini. Mehika. Continental uredništvo s.Do. od c.V. 20-34.
3. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7^ma. Izdaja. Mehika. Uredniki učenja Cengage. 21-39.