X kvadrat

Pojasnjujemo, kaj je x kvadrat, njegove lastnosti, primeri in vaje rešene

Območje kvadrata "x" strani je x kvadrat. Vir: f. Zapata.

Algebrsko delovanje "X kvadrat"Izvede se tako, da dvakrat pomnožimo količino" x ". Je del potencialnih operacij in v matematičnih simbolih je izražen na ta način:

x ∙ x = x²

To je poseben primer opolnomočenja, v katerem "x" predstavlja baza In "2" je eksponent. Če se v operaciji pojavi izraz x², Natančno se glasi kot "x kvadrat" ali "x kvadrat dvignjen".

Seveda so na primer možni drugi eksponenti, če je eksponent 3, potem je moč zapisana kot:

x ∙ x ∙ x = x³

In se preberite kot "x na tri", "x dvignjen na kocko" ali preprosto "x na kocko".

Na splošno je lahko eksponent, na katerega je podlaga visoka, poljubno število, imenovano "n", v tem primeru pa je napisana ustrezna moč:

xⁿ = x ∙ x ∙ x ∙… ∙ x

Tukaj suspendirane točke kažejo, da je treba "x" pomnožiti sam "n", torej tolikokrat, kot ga označuje eksponent.

Nekaj ​​preprostih primerov "x kvadrat" s številkami je naslednje:

3² = 3 ∙ 3 = 9

(−4)² = (−4) ∙ (−4) = 16

Kasneje so opisane različne aplikacije, za katere je potrebno.

Značilne lastnosti

Na splošno je produkt katere koli količine pri sebi, n Times, imenuje potencial. Izračun X kvadrata je le poseben primer potenciranja, dva druga primera se pojavita, ko želite znesek znesek zbrati na eksponent 1, pri čemer dobite enaka znesek:

Vam lahko služi: zakoni eksponentov

Ker so te operacije pogoste, za delo z bazami in eksponenti se upoštevajo nekaj preprostih pravil o obratovanju Zakoni eksponentov, ki so navedeni spodaj:

Zakoni eksponentov

V nadaljevanju sta "x" baza in "n" in "m" sta eksponenta.

1.- Produkt enakih osnovnih moči

Z pomnoževanjem dveh (ali več) moči enake osnove dobimo osnovo, dvignjeno na vsoto eksponentov:

xⁿ∙ x^m = x^n+m

V primeru X High se to pravilo uporablja na naslednji način, ki nadomešča N in M ​​za 1:

x¹∙ x¹ = x¹⁺¹ = x²

2.- Oddelek za napajanje enake baze

Z delitvijo moči iste baze se podlaga dobimo, dvignjeno na odštevanje med ustreznimi eksponenti števca in imenovalcem:

xⁿ ÷ x^m = x^N-m

Ker delitev z 0 ni definirana, jo je treba izpolniti, pod pogojem, da je x ≠ 0.

3.- Moč moči

Rezultat moči moči je enak podstavku, dvignjenem na produkt eksponentov:

(x^m)ⁿ = x^m∙n

Lahko dobite znova x kvadrat, ko delamo m = 1 in n = 2:

(x¹)² = x^1∙2 = x²

4.- Negativni eksponent

Za negativne eksponente je operacija, ki jo je treba izvesti:

Kadarkoli x ≠ 0. Upoštevajte, da v tem primeru moč postane delček s števcem, ki je enak 1.

5.- Delni eksponent

Delni eksponenti se lahko zapišejo kot nth koren baze:

Pod pogojem, da se n razlikuje od 0. Ta vrednost postane korenski indeks, medtem ko m postane eksponent količine pod korenino, kar je v tem primeru x.

Vam lahko služi: kakšna je smernica? (Geometrija)

Izdelki in količniki različnih baz

Ko morate izboljšati izdelke in količnike različnih baz "x" in "y", se sledijo ta pravila:

1.- Moč izdelka

Za izvedbo te moči se vsak znesek dvigne na eksponent N in vzpostavljen je nastali izdelek:

(x ∙ y)ⁿ = xⁿ ⋅ inⁿ

2.- Razmerje količnika

Ponovno je treba vsak znesek povečati na eksponent n ločeno in določiti količnik, ki ima za posledico pravilo, da se znesek "y" razlikuje od 0, v primeru pozitivnega "n":

(x ÷ y)ⁿ = xⁿ ÷ yⁿ

Kadar je "n" negativno, je treba biti previden zaradi premoženja 4 prejšnjega oddelka, števec postane imenovalec. V tem primeru morata biti oba zneska drugačna od 0, saj se je treba delitvi za 0 izogibati za vsako ceno.

Primeri

Primer 1: kvadratki naravnih številk

Kvadre prvih desetih naravnih številk so:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Primer 2: kvadrat negativnih številk

Kvadrat negativnega števila je vedno pozitiven, saj se pomnožita dve količini enakega znaka:

(-x) · (-x) = x ∙ x = x²

Na primer:

(-2) · (-2) = (-2)² = 4

Primer 3: kvadrat vsote in razlika

Pogosto je treba izračunati kvadrat vsote dveh količin ali njegovo razliko, ki so vključene v kategorijo pomembnih izdelkov.

Operacija se razreši z navedenimi indikacijami in pomočjo distribucijske lastnosti:

Kvadrat vsote

Naj bo dva "x" in "y" znesla in želite najti kvadrat njegove vsote (x + y)²:

Vam lahko služi: hierarhija operacij

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + in²

Ta izraz se glasi tako: "Kvadrat prvega in dvojni produkt prvega za drugi plus kvadrat drugega".

Kvadrat razlike

Rešeno je analogno, vendar upošteva negativni znak:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ in + in²

Primer 4: Območje kvadrata

Trg je 4 -stranski poligon, ki ima enak ukrep. Naj bo ℓ stranska meritev, potem je območje A na figuri podano z:

A = ℓ²

Primer 5: Teorem za pitagore

Ta teorem velja za pravokotnike trikotnike, tiste, na katerih dve strani tvorita ravna kot. Te strani so znane kot "kategorije", preostala pa je "hipotenuza".

Teorem določa, da je kvadrat hipotenuze enak vsoti kvadratov kategorij. Teorem je napisan kot: "A" in "B" v kategorije in "C" je napisan kot:

c² = a² + b²

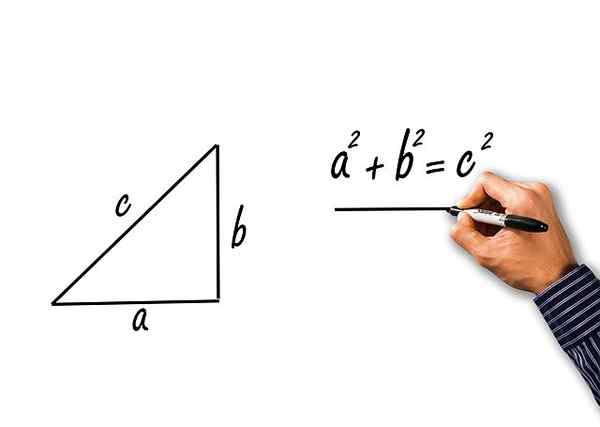Teorem Pythagora za pravokotni trikotnik mačk A in B, in hipotenusa c

Rešene vaje

Vaja 1

Izračunajte kvadrat hipotenuze, katere noge merijo 3 in 5 enot.

Rešitev

Po besedah ​​Pythagorasa je kvadrat hipotenuze:

c² = a² + b²

Zamenjava vrednosti:

c² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Vaja 2

Določite območje stranskega kvadrata ℓ = 6 cm

Rešitev

A = ℓ² = (6 cm)² = 36 cm²