Formule s povprečno hitrostjo, kako se izračuna in reši vaja

The Povprečna hitrost Za mobilni delček je opredeljen kot razlog med spreminjanjem položaja, ki ga doživlja, in časovnim intervalom, uporabljenim pri spremembi. Najpreprostejša situacija je tista, v kateri se delček premika po ravni črti, ki jo predstavlja os x.

Recimo, da mobilni objekt zaseda položaje X₁ in x₂ V časih t₁ in t₂ oziroma. Opredelitev povprečne hitrosti v_m Je matematično predstavljen na naslednji način:

Enote v_m V mednarodnem sistemu so metri/sekunde (m/s). Druge enote pogoste uporabe, ki se pojavljajo v mobilnih besedilih in napravah, so: km/h, cm/s, milje/h, stopala/s in še več, pod pogojem.

Grško pismo "Δ" bere "delta" in se uporablja za povzetek razlike med dvema količinama.

[TOC]

Značilnosti vektorja povprečne hitrosti V_m

Povprečna hitrost je pomembna značilnost gibanja. Vir: Pixabay

Povprečna hitrost je vektor, saj je povezana s spremembo položaja, ki je posledično znana kot Vektorski premik.

Ta kakovost je predstavljena krepko ali s puščico nad črko, ki označuje velikost. Vendar je v dimenziji edina možna smer osi x in se zato lahko izpusti z vektorskim zapisom.

Ker imajo vektorji velikost, smer in pomen, začetni pogled na enačbo kaže, da bo povprečna hitrost imela enako smer in smisel kot premik.

Predstavljajte si delček primera, ki se premika po ravni črti. Če želite opisati svoje gibanje, je treba navesti referenčno točko, ki bo "izvor" in bo označena kot ali ali.

Delci se lahko odmaknejo ali se približujejo ali pa levo ali na desno. Za dosego določenega položaja lahko uporabite tudi veliko ali malo časa.

Lahko vam služi: toplota: formule in enote, značilnosti, kako se meri, primeri

Omenjene velikosti: položaj, premik, interval časa in povprečna hitrost opisujejo vedenje delca med premikanjem. Gre za veličine Kinematična.

Za razlikovanje položajev ali lokacij na levi strani ali se uporablja znak (-) in tiste, ki jih najdemo na desni strani ali nosite znak (+).

Povprečna hitrost ima geometrijsko razlago, ki jo je mogoče videti na naslednji sliki. To je naklon črte, ki poteka skozi točke P in Q. Pri rezanju na položaj proti položaju. čas na dveh točkah, to je črta sušenje.

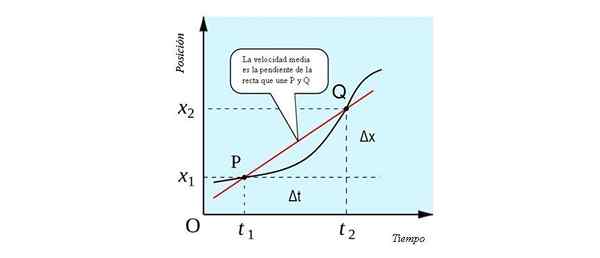Geometrijska razlaga povprečne hitrosti kot naklon črte, ki se pridruži P in Q točkam. Vir: すじにく シチュー [CC0].

Znaki povprečne hitrosti

Za naslednjo analizo je treba upoštevati t₂ > t₁. To pomeni, da je naslednji trenutek vedno večji od toka. Na ta način t₂ - t₁ Vedno je pozitiven, kar je običajno smiselno vsak dan.

Potem bo znak povprečne hitrosti določil x₂ - x₁. Opazite, da je pomembno.

Ali "naprej" ali "nazaj", kot bralec raje.

Če je povprečna hitrost pozitivna, to pomeni v povprečju vrednost "x”Sčasoma se povečuje, čeprav to ne pomeni, da bi se lahko v nekem trenutku v obravnavanem času zmanjšalo - ΔT -.

Vendar v globalnem smislu na koncu časa ΔT, Končala je z večjim položajem kot tista, ki jo je imela na začetku. Podrobnosti o gibanju se v tej analizi prezrejo.

Lahko vam služite: Newtonov tretji zakon: aplikacije, poskusi in vaje

Kaj pa, če je povprečna hitrost negativna? No, to pomeni, da se delček konča z manjšo koordinato kot tisto, s katero se je začel. Groso način se je premaknil nazaj. Poglejmo nekaj številčnih primerov:

Primer 1: Glede na začetne in končne položaje navedite znak povprečne hitrosti. Kam se je delček premikal po vsem svetu?

a) x₁ = 3 m; x₂ = 8 m

Odgovor: x₂- x₁  = 8 m - 3 m = 5 m. Pozitivna povprečna hitrost se je delček premaknil naprej.

b) x₁ = 2 m; x₂ = -3 m

Odgovor: x₂ - x₁ = -3 m -2 m = -5 m. Povprečna negativna hitrost se je delček premikal nazaj.

 c) x₁  = - 5 m; x₂ = -12 m

Odgovor: x₂ - x₁   = -12 m -( -5 m) = -7 m. Povprečna negativna hitrost se je delček premikal nazaj.

d) x₁  = - 4 m; x₂ = 10 m

Odgovor: x₂ - x₁  = 10 m - (-4m) = 14 m. Pozitivna povprečna hitrost se je delček premaknil naprej.

Ali je lahko povprečna hitrost 0? Ja. Dokler sta izhodišče in točka prihoda enaka. Ali to pomeni, da je bil delček ves čas nujno mirovan?

Ne, to pomeni le, da je bilo potovanje na krogu. Mogoče je potoval hitro ali morda zelo počasi. Za zdaj ni znano.

Povprečna hitrost: skalarna velikost

To nas vodi k določitvi novega izraza: Povprečna hitrost. V fiziki je pomembno razlikovati med vektorskimi magnitudami in magnitudami, ki niso: Scalars.

Za delček, ki je naredil krog, je povprečna hitrost 0, vendar bi lahko bila zelo hitra ali morda ne. Če želite vedeti, je povprečna hitrost opredeljena kot:

Enote povprečne hitrosti so enake kot pri povprečni hitrosti. Temeljna razlika med obema velikostma je, da povprečna hitrost vključuje zanimive informacije o smeri in smeri delca.

Lahko vam služi: fermionski kondenzat: lastnosti, aplikacije in primeri

Po drugi strani povprečna hitrost zagotavlja le številčne informacije. Z njo je znano, kako hitro ali počasi se je delček premikal, vendar ne, če je to storil naprej ali nazaj. Zato je skalarna velikost. Kako jih razlikovati, da jih označijo? Eden od načinov je, da se drzni za vektorje ali postavitev puščice nanje.

In pomembno je opozoriti, da povprečna hitrost ni treba biti enaka povprečni hitrosti. Za krožno potovanje je povprečna hitrost enaka nič, povprečna hitrost. Oba imata enako številčno vrednost, ko vedno potujeta v isto smer.

Vaja rešena

Domov se vračate iz šole tiho na 95 km/h na 130 km. Začnite dežurati in zmanjšuje hitrost na 65 km/h. Končno pride domov po vožnji 3 ure in 20 minut.

a) Kako daleč je vaš šolski dom?

b) kakšna je bila povprečna hitrost?

Odgovori:

a) Nekateri prejšnji izračuni so potrebni:

Potovanje je razdeljeno na dva dela, skupna razdalja je:

D = D1+ D₂, Z d1 = 130 km

Skupni čas je 3 ure in 20 minut = 3 + 1/3 ure = 10/3 ure = 3.33 h (iste enote je treba postaviti za čas, v tem primeru je to primerno).

T2 = 3.33 - 1.37 ur = 1.96 ur

Izračun d_2:

d₂ = 65 km/h x 1.96 h = 125. 4 km.

Šola je d1+ d₂ = 255.4 km od hiše.

b) Zdaj lahko najdete povprečno hitrost:

Reference

1. Giancoli, d. Fizika. Načela z aplikacijami. Šesta izdaja. Dvorana Prentice. 21-22.
2. Resnick, r. (1999). Fizično. Zvezek 1. Tretja izdaja v španščini. Mehika. Continental uredništvo s.Do. od c.V. 20-21.
3. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7ma. Izdaja. Mehika. Uredniki učenja Cengage. 21-23.