Opredelitev, zapisovanje, vaje Equinecent Vectors

Dva ali več Vektorji so oprema Če imajo isti modul, isto smer in enak smisel, tudi ko je njihova izvorna točka drugačna. Ne pozabite, da so značilnosti vektorja natančno: izvor, modul, smer in smisel. 

Vektorji so predstavljeni z orientiranim ali puščicam. Slika 1 prikazuje predstavitev več vektorjev v ravnini, od katerih so nekateri opremi v skladu s prvotno dano definicijo.

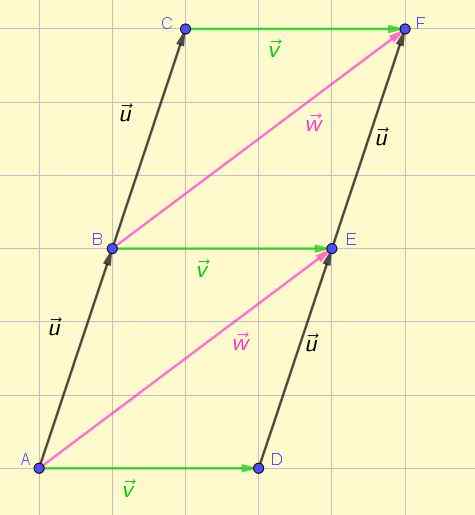Slika 1. Oprema in vektorje, ki niso pogostitev. Vir: Self Made.

Že od prvega pogleda je mogoče ceniti, da imajo trije zeleni vektorji enake velikosti, isto smer in enak smisel. Enako lahko potrdimo o dveh roza vektorjih in štirih črnih vektorjih.

Številne velikosti narave imajo vektorsko vedenje, takšno je primer hitrosti, pospeška in moči, če naštejemo le nekatere. Od tod tudi pomembnost njihovega pravilno karakterizacije.

[TOC]

Zapis za vektorje in opremo

Za razlikovanje vektorskih zneskov skalarnih zneskov se pogosto uporablja črna črka ali puščica na črki. Pri delu z ročnimi vektorji na prenosniku jih je treba razlikovati s puščico in ko se uporablja tiskani medij, se uporabljajo krepki.

Vektorji lahko zanikajo, kar kaže na njihovo izhodišče ali izvor in njihovo točko prihoda. Na primer Ab, Pr, Od in Ef Slika 1 pa so vektorji Ab, Pr, Od in Ef So skalarne količine ali številke, ki kažejo na velikost, modul ali velikost njihovih vektorjev.

Da bi navedli, da sta dva vektorja oprema, se uporablja simbol "∼ ". S to notacijo lahko na sliki opozorimo na naslednje vektorje, ki so med seboj opremo:

Vam lahko služi: kinetična energija: značilnosti, vrste, primeri, vaje

AB∼BC∼Ef 

Vsi imajo enako velikost, smer in pomen. Zato upoštevajte zgoraj navedene predpise.

Prosti, drsni in nasprotni vektorji

Kateri koli od vektorjev na sliki (na primer Ab) je predstavnik nabora vseh fiksnih vektorjev. Ta neskončni niz določa razred brezplačnih vektorjev ali.

ali = AB, BC, od, ef, ..

Alternativni zapis je naslednji:

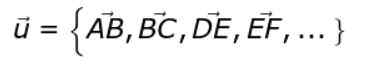
Če krepka ali puščica ni nameščena na vrhu ali, Se želimo sklicevati na vektorski modul ali.

Brezplačni vektorji se ne uporabljajo za določeno točko.

Za svoj del Drsni vektorji So opremo opreme za določen vektor, vendar mora biti njihova uporaba v vektorski akcijski liniji vsebovana.

In nasproti vektorjev So vektorji, ki imajo enako velikost in smer, vendar nasprotna čutila, čeprav se v angleških besedilih imenujejo nasprotni naslovi Ker naslov označuje tudi pomen. Nasproti vektorji niso oprema.

Vaje

-Vaja 1

Kateri drugi vektorji, prikazani na sliki 1?

Rešitev

Poleg tistih, ki so že navedeni v prejšnjem razdelku, na sliki 1 opazimo, da Oglas, Biti in Ec Med seboj so tudi vektorje:

Ad ∼ je ∼ ce 

Vsak od njih je predstavnik razreda brezplačnih vektorjev v.

Vektorji so tudi oprema med seboj Ae in Bf :

Ae ∼ Bf 

Ki so predstavniki razredov W.

-Vaja 2

Točke A, B in C so na kartezijanski ravnini XY in njihove koordinate so:

Vam lahko služi: idealen plin: model, vedenje, primeri

A = (-4.1), b = (-1.4) in c = (-4, -3)

Poiščite koordinate četrte točke D, tako da vektorji Ab in CD Biti oprema.

Rešitev 

Tako da CD biti oprema Ab mora imeti isti modul in isto smer kot Ab .

Modul Ab Square je:

|Ab|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

Koordinate D niso znane po tem, kar lahko rečemo: D = (x, y)

Nato: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

Kot |Ab| = |CD| Je eden od pogojev za Ab in CD Biti oprema, ki jo imate:

(x + 4)^2 + (y + 3)^2 = 18

Ker obstajata dva neznanka, je potrebna še ena enačba, ki jo je mogoče doseči iz pogoja, ki Ab in CD biti vzporedni in v istem smislu.

Vektor AB SLOPE

Vektorski naklon Ab označuje vaš naslov:

Čaka na AB = (4 -1)/(-1 -( -4)) = 3/3 = 1

Kar kaže, da je vektor Ab 45 ° oblikovanje z osi x.

CD vektorski naklon

Naklon CD Izračuna se podobno:

Čakajoča cd = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Ujemanje tega rezultata z naklonom Ab Imate naslednjo enačbo:

Y + 3 = x + 4 

Kar pomeni y = x + 1.

Če je ta rezultat nadomeščen v enačbi enakosti modulov, je:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Poenostavitev je:

2 (x+4)^2 = 18, 

Ki je enakovredno:

(x+4)^2 = 9

To je x+4 = 3, kar pomeni, da je x = -1. Tako da so koordinate D (-1, 0).

Preverite

Vektorske komponente Ab so (-1-(-4); 4 -1) = (3; 3)

Vam lahko služi: Thévenin teorem: kaj je sestavljeno, aplikacije in primeri

in tisti iz vektorja CD so (-1-(-4)); 0 -(-3)) = (3; 3)

Kar pomeni, da so vektorji oprema. Če imata dva vektorja enake kartezijanske komponente enak modul in smer, so torej oprema.

-Vaja 3

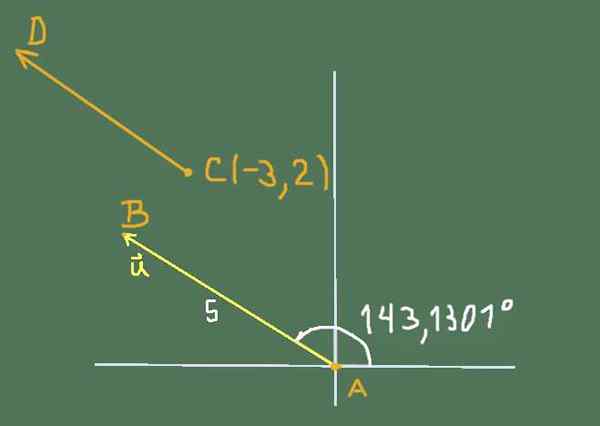
Prosti vektor ali ima velikost 5 in naslov 143,1301 °.

Poiščite njene kartezijanske komponente in določite koordinate točk B in C, ki vedo, da sta fiksni vektorji AB in CD oprema. Koordinate A so (0, 0) in koordinate točke C so (-3,2).

Rešitev 

Razmere, ki jih predlaga vaja, je lahko predstavljena z naslednjo sliko:

Slika 2. Diagram za reševanje vaje 3. Vir: Self Made.

Kartezijanske komponente ali so

ali = (5*cos (143,1301º); 5*greh (143,1301 °)) 

Izdelava izračunov ostaja:

ali = (-4; 3) 

B koordinate niso znane, zato bomo postavili B (x, y)

Vektorske koordinate Ab So (x-0; y-0), a ker je to opremo z u, je treba izpolniti enakost komponent, je torej sklenjeno, da so koordinate B (-4, 3).

Podobno vektorske koordinate CD so (x-(-3)); (in - 2) to mora biti oprema u, lali to vodi do:

 x + 3 = -4 in y -2 = 3

Potem bodo koordinate točke D (-7, 5).

Reference

1. Izračun.DC. Fiksni vektor. Brezplačni vektor. Iztegnjeno od: izračun.DC
2. 2d Descartes. Fiksni vektorji in prosti vektorji letala. Pridobljeno iz: Viri.izobrazba.je
3. Guao Project. Equinecent Vectors. Okreval od: Guao.org
4. Resnick, r., Krane, k. (2001). Fizika (v angleščini). New York: John Wiley & Sons.
5. Serway, r.; Jewett, John W. (2004). Fizika za znanstvenike in inženirje (v angleščini) (6. izdaja). Brooks/Cole.
6. Tupler, Paul a. (2000). Fizika za znanost in tehnologijo. Zvezek I. Barcelona: ed. Sem se obrnil.
7. Weisstein, e. "Vektor". V Weissteinu, Eric W. MathWorld (v angleščini). Wolfram Research.