Rezultat izračuna vektorja, primeri, vaje

On posledično vektor Je tisti, ki ga dobiva operacija z vektorji, katerih rezultat je tudi vektor. Običajno je ta operacija vsota dveh ali več vektorjev, skozi katere se pridobi vektor, katerega učinek je enakovreden.

Na ta način dobimo vektorji, kot so hitrost, pospešek ali sila. Na primer, ko več sil deluje na telo F₁, F₂, F₃,.. . Vektorska vsota vseh teh sil je enakovredna neto sili (posledično), ki se matematično izraža:

F₁ + F₂ + F₃ +… = F_R  tudi F_N

Slika 1. Teža snega je razporejena po stropu, njegovo delovanje pa lahko nadomestimo z eno samo silo, ki se uporablja na ustreznem mestu. Vir: Pixabay.

Nastali vektor, ne glede na to, ali gre za sile ali katero koli drugo vektorsko velikost, uporablja pravila vsote vektorjev. Ker imajo vektorji smer in smisel poleg številčne vrednosti, ni dovolj, da dodate module, da imajo nastali vektor.

To velja le v primeru, v katerem so vpleteni vektorji v isti smeri (glej primere). V nasprotnem primeru je treba uporabiti metode vektorske vsote, ki so lahko odvisno od primera geometrijske ali analitične.

[TOC]

Primeri

Geometrijske metode za iskanje nastalega vektorja so metoda poligona in paralelogramska metoda.

Kar zadeva analitične metode, je komponentna metoda, skozi katero je mogoče najti vektor, ki izhaja iz katerega koli vektorskega sistema, dokler imamo njegove kartezijske komponente.

Geometrijske metode za dodajanje dveh vektorjev

Predpostavimo, da vektorji ali in v (Porado jih označujemo, da jih ločimo od skalarne). Na sliki 2) jih imamo na ravnini. Na sliki 2 b) se je premaknil v Vector V tako, da njen izvor sovpada s koncem ali. Nastali vektor sega od izvora prvega (ali) na vrh zadnjega (v)::

Lahko vam služi: stisljivost: trdne snovi, tekočine, plini, primeri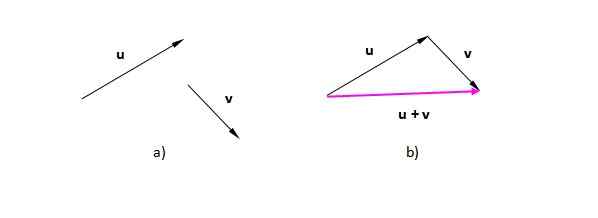 Slika 2. Nastali vektor iz grafične vsote vektorjev. Vir: Self Made.

Slika, ki ima v tem primeru, je trikotnik (trikotnik je 3 -stranski poligon). Če imamo dva vektorja v isti smeri, je postopek enak: postavite enega od vektorjev za drugim in narišite enega, ki gre od izvora ali repa prvega do konice ali konca zadnjega.

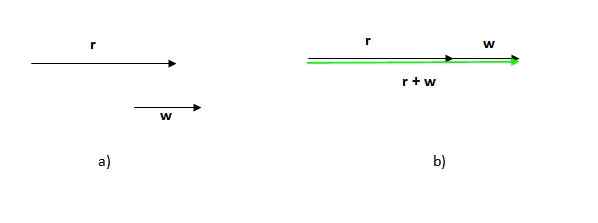
Upoštevajte, da vrstni red, v katerem je ta postopek, ni pomemben, saj je vsota vektorjev komutativna.

Upoštevajte tudi, da v tem primeru modul (Dolžina ali velikost) nastalega vektorja je vsota modulov dodatnih vektorjev, za razliko od prejšnjega primera, v katerem je nastali vektorski modul manjši od vsote modulov udeležencev.

Metoda paralelograma

Ta metoda je zelo primerna, ko morate dodati dva vektorja, katerih točke izvora se strinjajo, z izvorom koordinatnega sistema X-Y. Recimo, da gre za naše vektorje ali in v (Slika 3):

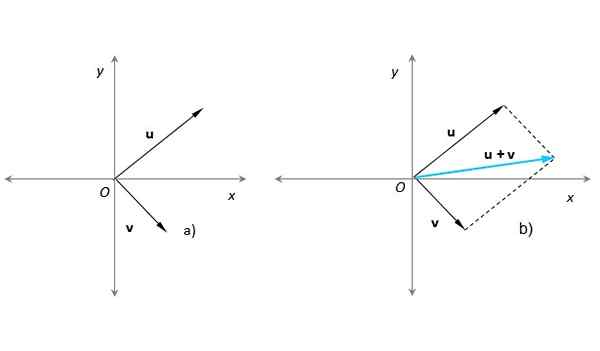Slika 3. Vsota dveh vektorjev s pomočjo paralelograma s pomočjo vektorja v turkizni modri. Vir: Self Made.

Na sliki 3b) je bil zgrajen paralelogram s pomočjo vzporednih pikčastih črt ali že v. Nastali vektor ima svoj izvor v O in koncu na mestu, kjer se pikčaste črte sekajo. Ta postopek je popolnoma enak tistemu, opisane v prejšnjem razdelku.

Vaje

-Vaja 1

Glede na naslednje vektorje poiščite dobljeni vektor s pomočjo poligonalne metode.

Lahko vam služi: svetlobni odsev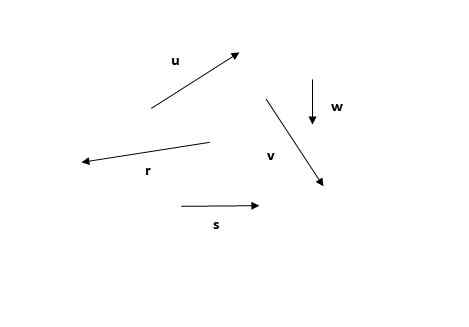 Slika 4. Vektorji, da bi našli svoje rezultate s poligonalno metodo. Vaja 1. Vir: Self Made.

Rešitev

Poligonalna metoda je prva od vidnih metod. Ne pozabite, da je vsota vektorjev komutativna (vrstni red dodatkov ne spremeni vsote), zato lahko začnete s katerim koli vektorjem, na primer ali (Slika 5a) oz r (Slika 5b):

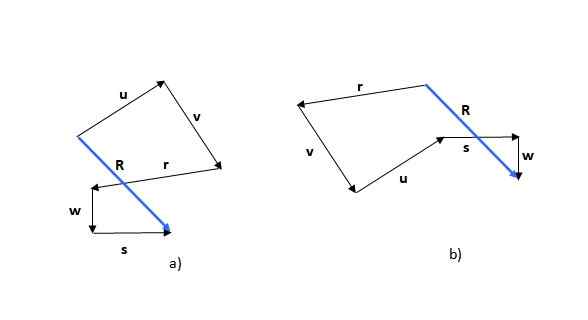Slika 5. Vsota vektorjev s poligonalno metodo. Vir: Self Made.

Pridobljena številka je poligon in dobljeni vektor (v modri barvi) se imenuje R. Če začnete z drugim vektorjem, je lahko oblikovana figura drugačna, kot je razvidno iz primera, vendar je nastali vektor enak.

Vaja 2

Na naslednji sliki je znano, da moduli vektorjev ali in v so u = 3 poljubne enote in v = 1.8 poljubnih enot. Kot to ali oblika s pozitivno osjo x je 45 °, medtem ko v oblikujejo 60 ° z osi y, kot je razvidno na sliki. Poiščite dobljeni vektor, velikost in smer.

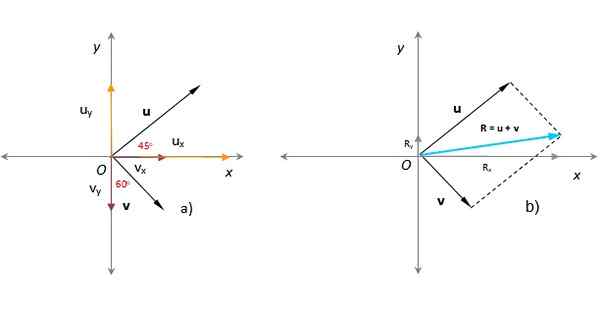
Rešitev

V prejšnjem razdelku je bil najdeni vektor, ki uporablja metodo paralelograma (na sliki v turkizi).

Preprost način, kako analitično najti dobljeni vektor, je izražanje vektorjev, ki dodajajo v smislu njihovih kartezijanskih komponent, kar je lahka naloga, kadar sta znana modul in kot, kot so vektorji tega primera:

ali_x = u . cos 45 ° = 3 x cos 45 º = 2.12; ali_in = u . greh 45 ° = 3x sen 45º = 2.12

v_x = v . Sen 60 ° = 1.8 x Sen 60 ° = 1.56; v_in = -V . cos 60 ° = -1.8 x cos 60 ° = - 0.9

Vam lahko služi: nihalo gibanje

Vektorji ali in v So vektorji, ki pripadajo ravnini, po obeh komponenti. Vektor U je v prvem kvadrantu in njene komponente so pozitivne, Vector V pa v četrtem kvadrantu; Njegova X komponenta je pozitivna, vendar njegova projekcija na navpični osi pade v osi in negativno.

Izračun kartezijanskih komponent dobljenega vektorja

Nastali vektor dodaja algebraično ustrezne komponente x in y, da pridobi svoje kartezijske komponente:

R_x = 2.12 + 1.56 = 3.68

R_in = 2.12 + (-0.9) = 1.22

Ko so kartezijanske komponente določene in je vektor popolnoma znan. Nastali vektor se lahko izrazi z zapisom v kvadratnih oklepajih (nosilci)::

R = poljubne enote

Notacija nosilca se uporablja za razlikovanje vektorja od točke v ravnini (ali v vesolju). Drug način izražanja nastalega vektorja na analitični način je z uporabo enotnih vektorjev Yo in j na letalu (Yo, J in k v prostoru):

R = 3.68 Yo + 1.22 J poljubne enote

Ker sta obe komponenti dobljenega vektorja pozitivni, vektor R Pripada prvemu kvadrantu, ki so ga že videli grafično.

Velikost in smer dobljenega vektorja

Znana za kartezijanske komponente, velikost R se izračuna skozi teorem pitagore, saj nastali vektor R, poleg svojih komponent r_x in r_in Tvorijo pravi trikotnik:

Velikost ali modul: r = (3.68² + 1.22²)^½ = 3.88

Naslov Q Vzamemo pozitivno osi X kot referenca: Q = Arcan (R_in / R_x) = ARCTG (1.22/3.68) = 18.3. mesto

Reference

1. Dodajanje vektorjev in pravil. Okrevano od: Newt.Phys.UNSW.Edu.Au
2. Figueroa, d. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika.31-68.
3. Fizično. Modul 8: Vektorji. Okrevano od: FRTL.UTN.Edu.ar
4. Hibbeler, R. 2006. Mehanika za inženirje. Statična. 6. izdaja. Continental uredništvo. 15-53.
5. Dodatni kalkulator vektor. Okrevano od: www.1728.org