Vektorske značilnosti in lastnosti, elementi, vrste, primeri

The vektorji So matematične entitete, ki imajo veliko -pozitivne -, ki jih običajno spremlja merska enota, poleg smeri in pomena. Takšne značilnosti so zelo primerne za opis fizičnih količin, kot so hitrost, moč, pospešek in še veliko več.

Z vektorji je mogoče izvajati operacije, kot so vsota, odštevanje in izdelki. Oddelek ni opredeljen za vektorje in kar zadeva izdelek, obstajajo trije razredi, ki jih bomo pozneje opisali: skalarni ali točkovni izdelek, vektor ali navzkrižni izdelek in produkt skalar za vektor.

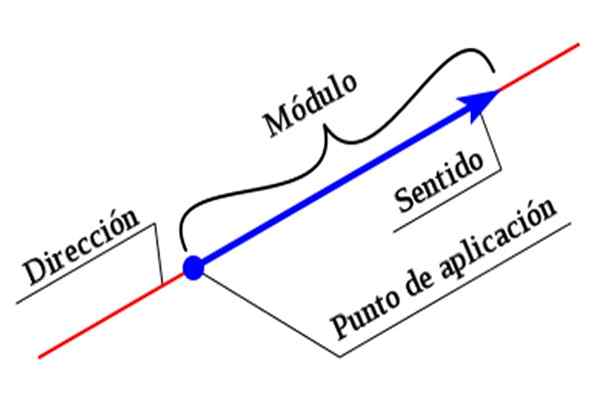Slika 1. Elementi vektorja. Vir: Wikimedia Commons.

Če želite v celoti opisati vektor, je treba navesti vse njegove značilnosti. Obseg ali modul je številčna vrednost, ki jo spremlja enota, medtem ko se s pomočjo koordinatnega sistema vzpostavita smer in pomen.

Poglejmo primer: Recimo, da letalo leti iz enega mesta v drugo s hitrostjo 850 km/h v smeri. Tu imamo popolnoma določen vektor, ker je na voljo velikost: 850 km/h, medtem ko sta smer in pomen ne.

Vektorji so običajno grafično predstavljeni z usmerjenimi segmenti linij, katerih dolžina je sorazmerna z velikostjo.

Medtem ko določite smer in pomen, je potrebna referenčna črta, ki je ponavadi vodoravna os, čeprav je sever lahko tudi kot referenca, takšen je primer hitrosti ravnine:

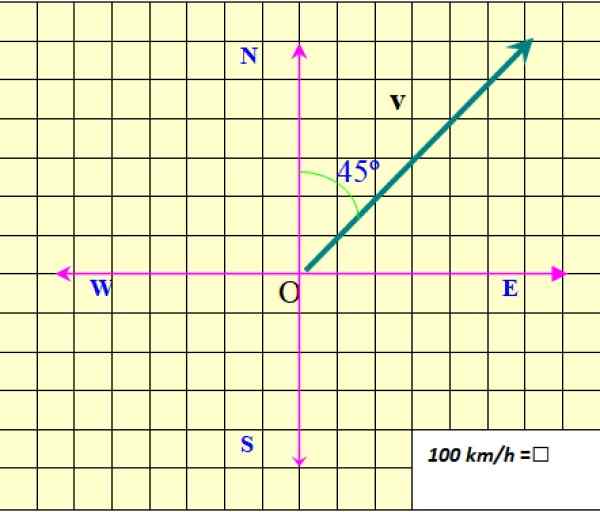Slika 2. Hitrostni vektor. Vir: f. Zapata.

Slika prikazuje hitrost vektorja ravnine, ki je označena kot v v drzno, da ga ločimo od skalarne količine, ki zahteva le številčno vrednost in nekatere enote, ki jih je treba določiti.

[TOC]

Elementi vektorja

Kot smo že rekli, so vektorski elementi:

-Magnitude ali modul, včasih imenovani tudi absolutna vrednost ali vektorski standard.

-Nagovor

-Smisel

Na primeru slike 2 je modul v Je 850 km/h. Modul je označen kot V brez krepkega ali kot |v|, Kjer palice predstavljajo absolutno vrednost.

Naslov v je določen glede na sever. V tem primeru je 45 ° severno od vzhoda (45 ° NE). Končno konica puščice obvesti o smeri v.

V tem primeru je bil vektorski izvor narisan tako, da je sovpadal z izvorom ali koordinatnim sistemom Povezani vektor. Po drugi strani pa, če se izvor vektorja ne ujema z referenčnim sistemom Brezplačni vektor.

Treba je opozoriti, da je treba za popolno določitev vektorja navesti te tri elemente, sicer bi bil opis vektorja nepopoln.

Pravokotne komponente vektorja

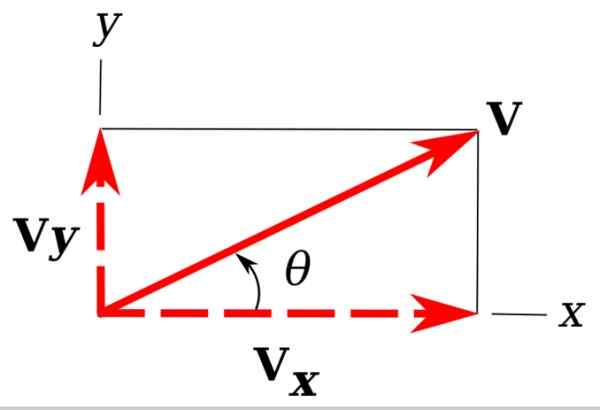Slika 3. Pravokotne komponente vektorja v ravnini. Vir: Wikimedia Commons. Unther [cc by-sa 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)]

Na sliki imamo nazaj naš primer vektorja v, to je v ravnini Xy.

Zlahka opaziti je, da v projekcije v koordinatnih osi x in y določajo pravi trikotnik. Te projekcije so v_in in v_x in se imenujejo pravokotne sestavine v.

Način označevanja v Skozi pravokotne komponente je tako: v = x, v_in>. Ti kvadratni oklepaji se uporabljajo namesto oklepajev, da se poudarijo dejstvo, da je vektor in ne točka, saj bi se v tem primeru uporabili oklepaje.

Vam lahko služi: James Chadwick: biografija, atomski model, poskusi

Če je vektor v tridimenzionalnem prostoru, je potrebna še ena komponenta, tako da:

v = x, v_in, v_z>

Če poznate pravokotne komponente, se izračuna velikost vektorja, kar je enakovredno iskanju hipotenuze desnega trikotnika, katerega noge so v_x in v_in,. Skozi teorem pitagore sledi:

|v|² = (v_x)² +  (v_in)²

Polarna oblika vektorja

Ko je znana vektorska velikost |v| In kot θ, ki je ta oblika z referenčno osi, običajno vodoravno os, vektor je enako določen. Nato se reče, da je vektor izražen v polarni obliki.

Pravokotne komponente v tem primeru se enostavno izračunajo:

v_x = |v|.cos θ

v_in = |v|.greh θ

V skladu z zgoraj navedenim pravokotnim komponentam hitrosti vektorja v letala bi bilo:

v_x = 850 . cos 45 ° km/h = 601.04 km/h

v_in = 850 . Sen 45 ° KM/H = 601.04 km/h

Fantje

Obstajajo različne vrste vektorjev. Obstajajo žili vektorji, položaj, premik, sila, električno polje, količina gibanja in še veliko več. Kot smo že povedali, je v fiziki veliko vektorskih velikosti.

Kar zadeva vektorje, ki imajo določene značilnosti, lahko omenimo naslednje vrste vektorjev:

-Nič: To so vektorji, katerih velikost je 0 in ki so označeni kot 0. Ne pozabite, da drzna črka simbolizira tri temeljne značilnosti vektorja, medtem ko običajna črka predstavlja samo modulu.

Na primer o telesu v statičnem ravnovesju, vsota sil mora biti ničelna vektor.

-Brezplačno in povezano: Prosti vektorji so tisti, katerih točke izvora in prihoda so kateri koli par točk ravnine ali prostora, za razliko od povezanih vektorjev, katerih izvor sovpada s pogledom na referenčni sistem, ki se uporablja za njihovo opisovanje.

Par ali trenutek, ki ga proizvaja nekaj sil, je dober primer prostega vektorja, saj navor ne velja za določeno točko.

-Oprema: To sta dva brezplačna vektorja, ki imata enake značilnosti. Zato imajo enako velikost, smer in pomen.

-Koplanares ali koplanarios: vektorji, ki pripadajo isti ravnini.

-Nasprotja: vektorji z enako velikostjo in smerjo, vendar nasprotna čutila. Vektor, ki nasprotuje vektorju v To je vektor -v In vsota obeh je ničelni vektor: v + (-v) = 0.

-Sočasno: vektorji, katerih akcijske linije prehajajo skozi isto točko.

-Zdrs: so tisti vektorji, katerih aplikacijska točka lahko drsi po določeni vrstici.

-Colineal: vektorji, ki se nahajajo na isti črti.

-Enota: Tisti vektorji, katerih modul je 1.

Vektorji ortogonalnih enot

Obstaja zelo uporabna vrsta vektorja v fiziki, imenovani ortogonalni vektor. Vektor ortogonalne enote ima modul, enak 1, enote.

Obstaja niz posebnih vektorjev, ki lažje predstavljajo druge vektorje in z njimi izvajajo operacije: to so vektorji pravokotne enote Yo, J in k, Enota in pravokotna drug na drugega.

V dveh dimenzijah so ti vektorji usmerjeni v celotnem pozitivnem smislu obeh osi x Od osi in. In v treh dimenzijah se v smeri osi doda enotni vektor z pozitivno. Zastopani so na naslednji način:

Vam lahko služi: kakšna je struktura dokumentarnih raziskav?

Yo =

J =

k =

Vektor je lahko predstavljen z enotnimi vektorji Yo, J in k kot sledi:

v = v_x Yo + v_in J + v_z k

Na primer vektor hitrosti v Iz prejšnjih primerov lahko zapišete kot:

v = 601.04 Yo + 601.04 J km/h

Komponenta v k Ni potrebno, saj je ta vektor v letalu.

Vsota vektorjev

Vsota vektorjev se pojavlja zelo pogosto v različnih situacijah, na primer, ko želite najti nastalo silo na predmetu, na katerega vplivajo različne sile. Za začetek predpostavimo, da imate dva prosta vektorja ali in v Na ravnini, kot prikazuje naslednje levo:

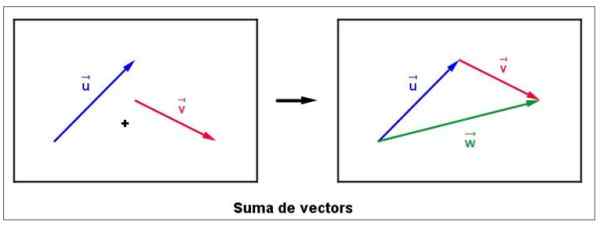Slika 4. Grafična vsota dveh vektorjev. Vir: Wikimedia Commons. LLUC Cabanach [CC BY-SA 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)].

Takoj se preseli v vektor v, ne da bi spremenili njegovo velikost, smer ali pomen, tako da izvira sovpada s koncem ali.

Vektor vsote se imenuje W in je narisano od u konca v, Glede na desno številko. Pomembno je opozoriti, da velikost vektorja W Ni nujno vsota velikosti v in ali.

Če se v zvezi s tem skrbno odraža, je edina priložnost, ko je velikost nastalega vektorja vsota velikosti dodatkov, ko sta oba odvisnika v isti smeri in imata enak pomen.

In kaj se zgodi, če vektorji niso brezplačni? Prav tako jih je zelo enostavno dodati. Način je dodajanje komponentne komponente ali analitična metoda.

Kot primer, upoštevajte vektorje naslednje številke, prva stvar je, da jih izrazimo iz ene od kartezijanskih oblik, ki je bila prej razložena:

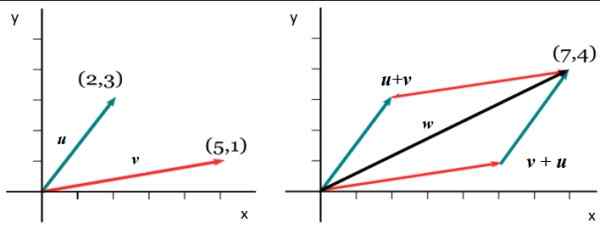Slika 5. Vsota dveh povezanih vektorjev. Vir: Wikimedia Commons.

v =

ali =

Pridobiti komponento v x vektorja doda W, Ustrezne komponente so dodane v x od v in ali: W_x = 5+2 = 7. In dobiti W_in Sledi analogni postopek: w_in = 1+3. Zato:

ali =

Lastnosti vsote vektorjev

-Vsota dveh ali več vektorjev povzroči drug vektor.

-Je komutativen, vrstni red dodatkov ne spreminja vsote, tako da:

ali + v = v + ali

-Nevtralni element vsote vektorjev je ničelni vektor: v + 0 = v

-Odštevanje dveh vektorjev je opredeljeno kot vsota nasprotnega: v - u = v + (-Or)

Primeri vektorjev

Kot smo že rekli, v fiziki obstajajo številne vektorske količine. Med najbolj znanimi so:

-Položaj

-Premik

-Povprečna hitrost in trenutna hitrost

-Pospešek

-Sila

-Količina gibanja

-Navor ali trenutek sile

-Impulz

-električno polje

-Magnetno polje

-Magnetni trenutek

Po drugi strani pa niso vektorji, ampak plezajo:

-Čas

-Masa

-Temperatura

-Glasnost

-Gostota

-Mehansko delo

-Energija

-Toplota

-Moč

-Napetost

-Električni tok

Druge operacije med vektorji

Poleg vsote in odštevanja vektorjev obstajajo še tri druge operacije med zelo pomembnimi vektorji, saj povzročajo nove zelo pomembne fizične velikosti:

-Produkt skalar za vektor.

-Skalarni izdelek ali točkovni izdelek med vektorji

-In križni ali vektorski izdelek med dvema vektorjem.

Produkt skalar za vektor

Razmislite o drugem zakonu, ki navaja to silo F in pospešek do So sorazmerne. Konstanta sorazmernosti je masa m predmeta torej:

F = m.do

Testo je skalar; Moč in pospeševanje sta vektorji. Ker si sila dobimo tako.

Vam lahko služi: primeri teoretičnega okvira

Ta vrsta izdelka vedno povzroči vektor. Tukaj še en primer: količina gibanja. Biti Str Vektorska količina gibanja, v Vektor hitrosti in kot vedno, m je masa:

Str = m.v

Skalarni izdelek ali točkovni izdelek med vektorji

Mehansko delo smo uvrstili na seznam velikosti, ki niso vektorji. Vendar je delo v fiziki rezultat delovanja med vektorji, imenovanimi skalarni izdelki, notranji ali točkovni izdelek.

Biti vektorji v in ali, Točka ali plezalni izdelek je opredeljen med njimi:

v∙ali = |v| ∙ |ali |.cos θ

Biti θ kot med njimi. Iz enačbe, ki je prikazana, se takoj ugotovi, da je rezultat točkovnega izdelka skalarna in tudi, da če sta oba vektorja pravokotna, je njihov skalarni izdelek 0.

Nazaj na mehansko delo W, To je skalarni izdelek med trdnim vektorjem F in vektorski premik ℓ.

W = F∙ℓ                  

Ko so vektorji na voljo glede na svoje komponente, je točkovni izdelek tudi zelo preprost za izračun. Ja v = x, v_in, v_z > in ali = x, ali_in, ali_z >, Točkovni izdelek med obema je:

v∙ali = v_x ali_x + v_in ali_in + v_z ali_z

Točkovni izdelek med vektorji je torej komutativen:

v∙ali = ali∙v

Navzkrižni izdelek ali vektorski izdelek med vektorji

Ja v in u sta naša dva primera vektorja, vektorski izdelek je opredeljen kot:

v x ali = W

Takoj sledi, da navzkrižni izdelek povzroči vektor, katerega modul je opredeljen kot:

|v x u | = | V | . | u |. greh θ

Kje θ Je kot med vektorji.

Križni izdelek torej ni komutativen v x u ≠ u x v. Pravzaprav v x U = - (u x V).

Če sta dva primera vektorja izražena v smislu vektorjev enot, je olajšan izračun vektorskega izdelka:

v = v_x Yo + v_in J + v_z k

ali = u_x Yo + ali_in J + ali_z k

Prečkamo izdelke med enotami

Križni izdelek med enakimi enotami je ničen, saj je kot med njimi 0 °. Toda med različnimi enotami je kot med njimi 90 ° in Sin 90 ° = 1.

Naslednja shema pomaga najti te izdelke. V smeri puščice je pozitivno smiselno in v nasprotni smeri:

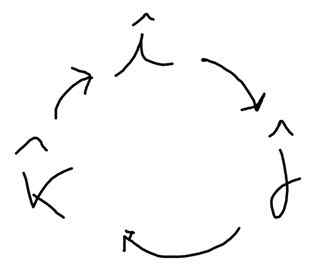
Yo x J = K, J x k = Yo; k x Yo = J; J x i = -k; k x J = -Yo; Yo x k = -J

Uporaba distribucijske lastnosti, ki ostaja veljavna za izdelke med vektorji in lastnosti enotnih vektorjev, imate:

v x ali = (v_x Yo + v_in J + v_z k) X (u_x Yo + ali_in J + ali_z k) =  

= (v_inali_z - v_zali_in )Yo + (v_zali_x - v_xali_z )J + (v_xali_in - v_inali_x )k

Rešene vaje

- Vaja 1

Glede na vektorje:

v = -5 Yo + 4J + 1 k

ali = 2 Yo -3 J + 7k

Kakšen bi moral biti vektor W tako da vsota v + ali + W rezultati 6 Yo +8 J -10k?

Rešitev

-5 Yo + 4J + 1 k

2 Yo -3 J + 7k

 W_x Yo + W_in J + W_z k  +

--

6Yo + 8 J -10 k

Zato je treba izpolniti:

-5 +2 + W_x = 6 → W_x = 9

4-3 + w_in = 8 → W_in = 7

1 + 7 + W_z = -10 → W_z = -18

Odgovor je: W = 9 Yo +7 J - 18k

- Vaja 2

Kakšen je kot med vektorji v in ali vaje 1?

Rešitev

Uporabili bomo skalarni izdelek. Imamo:

cos θ = v∙ali / |v| ∙ |ali|

v∙ali= -10 -12+7 = -15

|v| = √ (-5)² +4² +1²= √42 = 6.48

|ali| = √2² +(-3)² +7²= √62 = 7.87

Zamenjava teh vrednosti:

cos θ = -15 / 6.48 x 7.87 = -0.2941 → θ = 107.1

Reference

1. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
2. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
3. Rex, a. 2011. Osnove fizike. Pearson.
4. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.
5. Serway, r., Jewett, J. 2008. Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.