Koncept linearne variacije, primeri, rešena vaja

The Linearna variacija Pojavi se med dvema fizičnimi velikostmi, ko je graf, ki jih predstavlja. Enako je potrditev, da so spremenljivke v linearni odvisnosti, tako da če ga eden od njih imenujemo "y", drugi "x" pa bodo povezani z matematičnim izrazom:

y = mx + b

V tej formuli sta M in B realne številke. Vrednost m predstavlja naklon ali naklon črte - ki je vedno konstantna - in B je rez črte z navpično osjo.

Linearna variacija ene magnetu glede na drugo pomeni, da je njegov graf ravno črta. Vir: Joulegio/cc by-s (https: // createCommons.Org/licence/by-sa/4.0

Vsak pojav, ki se odziva na linearno variacijo, ima različna imena za spremenljivke, kot bomo videli v naslednjih primerih. Vendar je matematična oblika enačbe enaka.

Eksperimentalno je mogoče ugotoviti, če obstaja linearno razmerje med dvema velikosti, ki merijo pare vrednosti (x, y).

Pridobljene točke so grafične v milimetrskem papirju in jih opazimo, če imajo linearni trend, to je, če obstaja črta, ki se ustrezno prilagodi eksperimentalnim podatkom.

Najprej je mogoče to vrstico narisati vizualno, vendar s pomočjo linearna regresija Analitično jih je mogoče najti, vrednosti M in B črte, ki najbolje ustrezajo eksperimentalnim točkam.

[TOC]

Primeri linearne variacije

Obstajajo številni naravni pojavi, pa tudi vzpostavljeni odnosi med merilnimi vzorci, ki na primer upoštevajo linearno variacijo:

Hitrost v enakomerno raznolikem pravokotnem gibanju

Hitrost, odvisno od časa V (t) mobilnega telefona, ki se premika po črti s konstantnim pospeševanjem pri in začetni hitrosti V_tudi  drugačen od 0. To gibanje je znano kot enakomerno raznoliko pravokotno gibanje In enačba hitrosti je:

Vam lahko služi: gostota

v (t) = v_tudi + Ob

Toplotno raztezanje

Drug naravni pojav, katerega sprememba je linearna, je povečanje dolžine, ki doživlja palico ali žico pri segrevanju.

Dejansko, ko se temperatura katerega koli predmeta poveča, je tudi njene dimenzije in to povečanje odvisno od spremembe temperature ΔT in zneske, imenovane količine Linearni koeficient dilatacije označeno z grško črko α:

L = l_tudi + α ΔT

V tem izrazu je L končna dolžina predmeta in l_tudi je njegova začetna dolžina.

Položaj mobilnega telefona s konstantno hitrostjo

Mobilni telefon z hitrost Konstanta se vedno premika v ravni črti. Če je ravna črta vodoravna os x, je položaj x (t) v vsakem trenutku podan z:

x (t) = x_tudi + Vt

Kjer x_tudi To je začetni položaj, V je hitrost in T je čas. Na ta način se reče, da se položaj X linearno razlikuje glede na čas t.

Oseba stas

Zdravniki in antropologi lahko ocenijo stas človeka z merjenjem dolžine stegnenice.

Višja kot je oseba, dlje kot imajo noge, zato obstajajo linearni modeli, ki napovedujejo višino odrasle osebe H (v palcih), če je po enačbi znana dolžina L (tudi v palcih) svoje stegnenice

H = 1.880⋅L + 32.010

Temperaturne lestvice

Tehtnice Celzija in Fahrenheita se vsakodnevno uporabljajo za merjenje temperatur. Ta zadnja lestvica se običajno uporablja v angleško govorečih državah. Obstaja enakovrednost, ki se premika od enega v drugega:

F = (9/5) C + 32

Kjer je F temperatura v stopinjah Fahrenheit in C je temperatura v stopinjah Celzija.

Pritisk in globina

Absolutni tlak P v nestisljivi tekočini, kot je voda, katere konstantna gostota je ρ, se razlikuje glede na globino h kot:

Lahko vam služi: horizontalno streljanje: značilnosti, formule in enačbe, vaje

P = p_tudi + ρgh

Kjer p_tudi Je pritisk na prosti površini tekočine. Če je tekočina v posodi, ki je odprta za atmosfero, je ta tlak preprosto atmosferski tlak P_Bankomat, Takrat biti sposoben pisati:

P = p_Bankomat + ρgh

Atmosferski tlak na morskem nivoju je približno 101 kPa. To razmerje med P in H pomeni, da se tlak linearno povečuje z globino.

Tlak, ki ga doživlja potapljač, se linearno spreminja z globino. Vir: Ahmed Samy/Pexels.

Vaja rešena

Stroški vožnje

Mesečni stroški upravljanja z avtomobilom vključujejo mesečne fiksne stroške C_tudi plus stroški kilometrine ali kilometrine, ki so potovali vsak mesec. Voznik opaža, da so v enem mesecu stroški upravljanja znašali 380 dolarjev za 480 dolarjev, naslednji mesec pa 460 dolarjev na 800 milj.

Naj voznik prevozi znesek kilometrov na mesec s predloženimi podatki, poiščite:

a) linearna variacija med C in D.

b) Koliko bi avtomobil stal na mesec na 1500 milj?

c) Graf C v primerjavi z D.

Rešitev

Recimo, da imajo spremenljivke razmerje, ki ga daje:

C = c_tudi + Do.d

Kjer a in c_tudi So konstantne za določanje. A je naklon črte, ki grafično predstavlja razmerje med C in D. CO je rezanje z navpično osi, mesečni fiksni stroški, ki jih mora voznik plačati za samo dejstvo, da ima avtomobil na voljo. Tu lahko na primer vključimo vzdrževanje in davčni stroški.

Če želite nedvoumno določiti črto, je treba vedeti, da je pobočje. Za to imamo točke:

Str₁: 480 milj, 380 USD

Str₂: 800 milj, 460 dolarjev

Te točke koordinat (d, c) ali (razdalja, stroški) so analogne koordinatnim točkam (x, y) kartezijanske ravnine, kar se spremeni imena. Nagib na črto je nato:

Vam lahko služi: nagnjeno letalo

A = (c₂ - C₁)/(D₂ - d₁)

A = [(460 - 380) $ / (800 - 480) milj] = (1/4) $ / milja

Naklon črte predstavlja stroške na miljo na ta način:

C = c_tudi + Do.D = co + (1/4).d

Za določitev osnovnih stroškov c_tudi Ta enačba je vzeta in ena od točk, ki jo poznamo, pripada, na primer str₁:

380 $ = c_tudi + [(1/4) $ / milja] . 480 milj → 380 $ = c_tudi + 120 $

C_tudi = 260 USD

Zdaj lahko oblikujemo model linearne variacije, kot je:

C = 260 + (1/4) d

Rešitev b

Mesečni stroški potovanja 1500 milj so:

C = 260 + (1/4) x 1500 $ = $ 635

Rešitev c

Graf C kot funkcija D je:

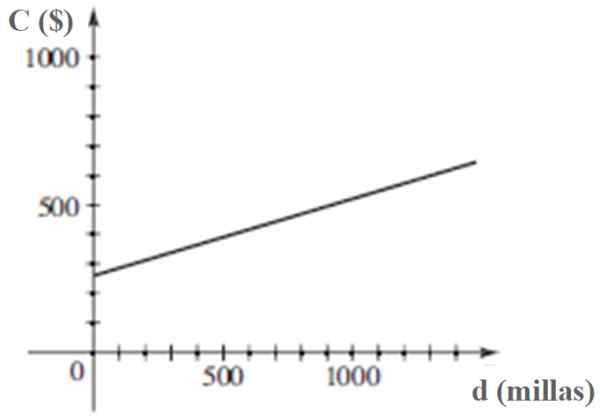Stroški upravljanja vozila so linearna funkcija prevožene razdalje D. Vir: Stewart, J. Prekalenkulacija.

Reference

1. Baldor. 1977. Elementarna algebra. Venezuelske kulturne izdaje.
2. Hoekenga, c. Linearne enačbe v znanosti. Okrevano od: Visionlearning.com.
3. Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
4. Jiménez, r. 2008. Algebra. Dvorana Prentice.
5. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
6. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.