Karakteristike trenutne vrednosti, formule in primeri

On trenutna vrednost (VA) je sedanja vrednost prihodnjega zneska denarja ali denarnih tokov ob upoštevanju posebne stopnje dobičkonosnosti, začenši v času vrednotenja. Pri računovodstvu je to koncept kazalnika, tako da se sredstva in obveznosti merijo na trenutno vrednost, do katere bi jih lahko prodali ali likvidirali do trenutnega datuma.

Prihodnji zneski se morajo spoprijeti z inflacijskimi ali deflacijskimi pritiski, z priložnostnimi stroški in drugimi tveganji, ki vplivajo na vrednost končnega zneska. Resnična enakovredna vrednost zneska v prihodnosti ne bo enaka zneska kot vsota denarja danes. Tam se začne igrati trenutna vrednost.

Vir: Pixabay.com

Če imate oceno, kaj bi danes lahko pridobili z naložbo, je enostavno oceniti, koliko bi bila vredna te prihodnje vrednosti. Sedanja vrednost kaže tudi na znesek, ki bi bil potreben za vlaganje danes, če želite končati s končnim globalnim zneskom, ob predpostavki, da je določena uspešnost.

[TOC]

Značilnosti

Investitor, ki ima denar, ima dve možnosti: porabite zdaj ali ga prihranite. Finančno nadomestilo za njegovo varčevanje in ne porabo, da se bo denarna vrednost nabrala z sestavljenimi obrestmi, ki jih boste prejeli od posojilojemalca ali banke.

Zato za oceno realne vrednosti zneska denarja danes po določenem obdobju gospodarski agenti združijo znesek denarja po določeni obrestni meri.

Delovanje ocenjevanja trenutne vrednosti v prihodnji vrednosti se imenuje kapitalizacija. Na primer, koliko bo trenutna $ vreden v 5 letih?

Obravnava operacija, ki ocenjuje trenutno vrednost prihodnjega zneska denarja, se imenuje popust. Na primer, koliko jih bo 100 dolarjev prejelo v 5 letih, danes na loteriji?

Vam lahko služi: nadomestni izdelki: značilnosti in primeri

Trenutna vrednost v računovodstvu

Trenutna vrednost je uporabna, kadar je bilo dolgotrajno obdobje prekomerne inflacije. V teh pogojih bodo zgodovinske vrednote, v katerih so bile zabeležene sredstev in obveznosti, verjetno precej nižje od njihovih trenutnih vrednosti.

Vendar ni visoke stopnje sprejemanja koncepta trenutne vrednosti pri računovodstvu. Predstavlja naslednje težave:

Računovodski stroški

Čas je potreben za nabiranje trenutnih informacij o vrednosti. Zato to poveča stroške in čas, povezan z ustvarjanjem računovodskih izkazov.

Razpoložljivost informacij

Morda je težko ali nemogoče pridobiti informacije o trenutni vrednosti o nekaterih sredstvih in obveznostih.

Natančnost informacij

Določene informacije o trenutni vrednosti lahko temeljijo manj na dejstvih in bolj na predpostavkah ali slabo utemeljenih ocenah, kar vpliva na zanesljivost računovodskih izkazov, ko so vključene te informacije.

Formule

Trenutna vrednost je formula, ki se uporablja pri financah, ki izračuna sedanjo vrednost zneska, ki bo prejet na prihodnji datum. Predpostavka enačbe je, da obstaja "vrednost denarja sčasoma".

Vrednost denarja sčasoma je koncept, ki kaže, da je danes prejemanje več kot prejemanje tega istega članka na prihodnji datum.

Domneva je, da je danes zaželeno prejeti 100 USD kot da v enem letu prej prejmete enako količino denarja. Vendar pa se zgodi, če so bile možnosti med prejemanjem 100 USD v sedanjosti ali 106 USD na leto od danes?

Potrebna je formula, ki lahko zagotovi merljivo primerjavo med trenutnim zneskom in zneskom v prihodnjem času glede na svojo trenutno vrednost.

Vam lahko služi: ekstraktivne dejavnosti: značilnosti, vrste in primeri

Va = fn / (1+r) ^n, kjer

Fn = prihodnja vrednost v obdobju n.

R = stopnja donosa ali dobičkonosnost.

n = število obdobij.

Uporaba formule

Formula trenutne vrednosti ima široko paleto uporabe. Zato ga je mogoče uporabiti na različnih finančnih področjih, vključno s financami podjetij, bančništvom in naložbami. Uporablja se tudi kot sestavni del drugih finančnih formul.

Kako se izračuna trenutna vrednost?

Recimo, da imate trenutno 1000 in 10% letnih obresti. To pomeni, da denar vsako leto raste 10%, na tak način:

$ 1000 x (10%= 100) = 1100 $ x (10%= 110) = $ 1210 x (10%= 121) = $ 1331 itd.

-Prihodnje leto bo 1100 dolarjev zdaj enakih 1000 USD.

-Čez dve leti bo 1210 dolarjev zdaj enakih 1000 USD.

-V treh letih bo 1331 dolarjev zdaj enakih 1000 USD.

Pravzaprav bodo vsi ti zneski pravočasno enaki, če upoštevamo, kdaj se pojavijo, in z 10% letnimi obrestmi.

Namesto da vsako leto dodate 10%, je lažje pomnožiti do 1,10. Na ta način je pridobljeno naslednje: 1000 $ x 1,10 = $ 1100 x 1,10 = $ 1210 x 1,10 = $ 1331 itd.

Do zdaj izračunajte prihodnjo vrednost

Če želite vedeti, kakšen denar je v prihodnosti vredno, se izračuna nazaj, vsako leto se deli z 1,10, namesto da se pomnoži.

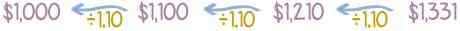
Recimo, da bo obljubljeno, da bo prihodnje leto plačal 500 USD. Obrestna mera je 10%. Če želite vedeti, kakšna je vrednost tega zneska danes, je prihodnja vrednost 500 USD razdeljena z 1,10, saj je enaka 454,55 USD kot trenutna vrednost.

Recimo, da je obljubljeno, da bo v treh letih plačal 900 dolarjev. Da bi danes vedeli vrednost tega zneska, je ta prihodnji znesek razdeljen z 1,10 trikrat. Tako bi bilo 900 USD v 3 letih: 900 ÷ 1,10 ÷ 1,10 ÷ 1,10 = $ 900 ÷ (1,10 × 1,10 × 1,10) = $ 900 ÷ 1,331 = 676,18 $ zdaj zdaj.

Vam lahko služi: vrtenje zalog

Primeri

Primer 1

Posameznik želi ugotoviti, koliko denarja bi moralo dati na svojem računu na denarnem trgu, da bi danes v enem letu pridobil 100 USD, če zasluži 5% obresti na njihovem računu.

100 USD, ki bi jih rad prejel v enem letu, označuje del F1 formule, 5% bi bilo r, število obdobij pa bi bilo preprosto 1. Če to postavite v formulo, bi bilo VA = 100 USD / 1,05 = 95,24 USD. Danes bi moral deponirati 95,24 USD, da bi v enem letu pridobil 100 USD, po 5 -odstotni obresti.

Primer 2

Recimo, da se danes znesek odloži na računu, ki letno zasluži 5% obresti. Če je cilj imeti 5 dolarjev.000 na računu ob koncu šestih let želite vedeti, koliko bi morali danes položiti na račun. Za to se uporablja formula trenutne vrednosti:

Trenutna vrednost = prihodnja vrednost / (1 + obrestna mera) ^ Število obdobij.

Če vstavite znane podatke, imate:

VA = 5 USD.000 / (1 + 0,05) ^ 6 = $ 5.000 / (1.3401) = 3 USD.731.

Reference

1. Steven Bragg (2018). Računovodstvo trenutne vrednosti. Računovodska orodja. Vzeti od: AccountingOols.com.
2. Finančne formule (2019). Trenutna vrednost. Vzeto iz: FinanceFormulas.mreža.
3. MATHSISFUN (2019). Sedanja vrednost (PV). Vzeto od: MathSisFun.com.
4. DQYDJ (2019). Sedanji kalkulator vrednosti in razlaga sedanjosti formule. Vzet od: dqydj.com.
5. Pamela Peterson (2019). Primer sedanje vrednosti. Univerza James Madison. Vzeto od: Educa.Jmu.Edu.
6. Wikipedia, brezplačna enciklopedija (2019). Trenutna vrednost. Vzeto od: v.Wikipedija.org.