A Rhomboid To je ravna figura štirih strani, -a štirikotnikov, ki so njene strani in notranji koti različni dve do dva. Zato romboid spada v skupino poševnih paralelogramov.

Geometrijske figure so del narave in zlasti tistih s štirimi stranmi, kot je Rhomboid, imajo veliko aplikacij v arhitekturi in oblikovanju.

Slika 1. Svetlobne plošče stadiona Allianz Arena v Münchnu v Nemčiji se osvetljujejo z barvami lokalne ekipe in z belo svetlobo, ko igra izbor te države. Vir: pxhere.

Zgoraj imamo del fasade nogometnega stadiona Allianz Arena v Münchnu. So romboidne plošče, ki se prižgejo z barvami lokalne ekipe.

Zato je figura z veliko vizualne dinamike, saj za razliko od drugih kvadrilateralov nima osi simetrije. Naslednja slika prikazuje različne romboide z raznolikimi usmeritvami v ravnini.

Slika 2. Več romboidov z različnimi usmeritvami v ravnini. Vir: f. Zapata.

[TOC]

Romboidne značilnosti

Nato glavne značilnosti te zanimive geometrijske figure:

-Številka lista: 4.

-Število vrhov: 4.

-Nasprotne strani so enake in vzporedne, vendar so sosednje strani neenake.

-Ima 4 notranje kote: dva akutna (manj kot 90 °), označena z grško črko α in dvema trmama (nad 180 °), imenovana β (glej sliko 3).

-Z dodajanjem dveh sosednjih kotov romboida dobimo 180 °, zato sta α in β Dopolnilno.

-Vsota 4 notranje kote je enaka 360 °.

-Diagonala je segment, ki se začne z vrhom in se konča na nasprotnem vrhanju.

-Točka, v kateri se imenuje diagonala sekanja romboida Barycenter.

-Diagonale Rhomboid imajo različne velikosti.

O diagonalih Rhomboida je nekaj pomembnih podrobnosti, o katerih bomo razpravljali spodaj.

Vam lahko služi: do vrstice: formula in enačbe, zastopanost, primeri

Diagonale romboida

Zelo pomembno je poudariti, da diagonale romboidov niso bisektrične, to je, da notranjega kota figure ne delijo na dva enaka dela.

Diagonale med seboj niso pravokotne. Vendar jih lahko enostavno izračunamo s kosinusnim teoremom. Tako glavna diagonala d_M V romboidu slike 3 je:

D_M = √ (a² + b² - 2.Ab.cos β)

In manjša diagonala d_m Jaz bi bil:

D_m = √ (a² + b² - 2.Ab.cos α)

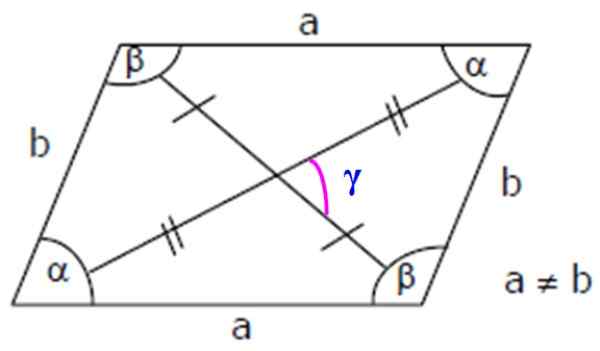Slika 3. Romboidni elementi: stranice, notranji in diagonalni koti. Vir: Wikimedia Commons.

Pomembno: Ker sta α in β dopolnita, je izpolnjeno:

sin α = sin β

cos α = -cos β

Te lastnosti trigonometričnih razlogov je treba upoštevati pri reševanju vaj.

Kako vzeti obod in območje

Če želite najti obod in območje, bomo dali ime strani romboida do in b. Imamo tudi višino romboida, imenovano h, ki je črta, izvlečena iz enega od vrhov in pravokotno usmerjena na nasprotno stran slike.

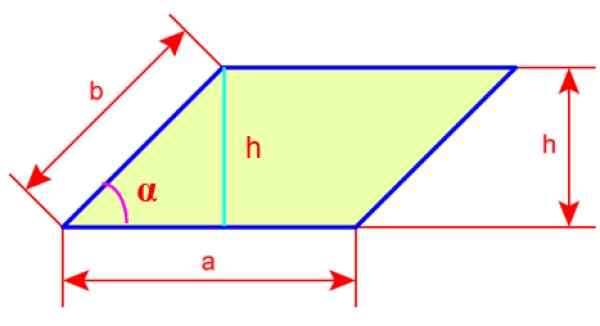Slika 4. Strani in višina romboida. Vir: Wikimedia Commons.

Obod romboida

Obod romboida se izračuna z dodajanjem dolžin njegovih štirih strani. Pokličimo P na obod, potem:

P = 2a + 2b

Lahko ga tudi izrazimo skozi:

P = 2 (a+b)

Obod, ki pozna višino

Če je dobro videti, lahko višino H določimo iz trikotnika na levi strani na sliki 4. Strani B bi bila hipotenuza in višina H Cateto, ki nasprotuje kot α, torej:

sin α = nasproti / hipotenusa cateto

O No:

sin α = h / b

Potem smo razčistili B:

b = H / sin α

Zamenjamo v obodu P:

P = 2 [a + (h / sin α)]

Območje romboida

Rhomboidno območje je merilo njegove površine. In ker gre za paralelogram, je njegovo območje A podano z dobro znanim izrazom:

Vam lahko služi: skupni dejavnik za razvrščanje izrazov: primeri, vaje

A = osnovna x višina

Da se po slikah 3 in 4 izraža skozi:

A = a x h

Območje, ki pozna obe strani in notranji kot

Z uporabo osnovne trigonometrije prejšnjega razdelka najdemo enakovredne izraze za območje Rhomboida:

h = b. greh α

Potem je območje takšno:

A = a. b. greh α

Če se spomnimo tega, kar smo povedali zgoraj o dodatnih kotih, lahko po potrebi nadomestimo sen α s sen β.

Območje, ki poznajo diagonale in kota med njimi

Končno, če poznamo diagonale d_M in d_m, Plus kot γ med njimi (glej sliko 3), lahko območje izračunamo s polproduktom diagonalov skozi krog omenjenega kota:

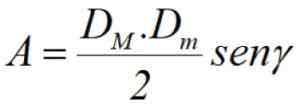
Vaja rešena

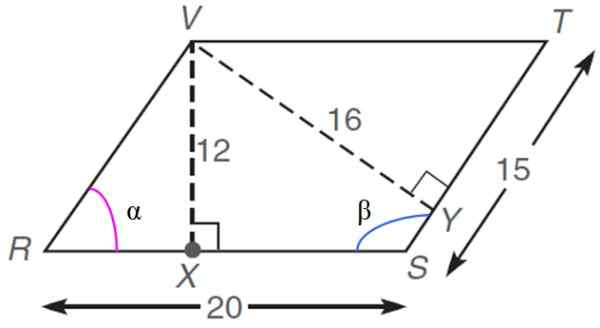
V naslednjem Rhomboidu, katerega dimenzije so podane v poljubnih enotah oz.do., najti:

a) vrednost oboda

b) Območje

c) Notranji koti α in β

d) Dolžina segmenta RX

e) Ukrep vsake diagonale

Rešitev

Obod P je:

P = 2 (a + b)

Najprej prepoznamo vrednosti A in B:

A = 20

B = 15

Zamenjamo formulo in izračunamo:

P = 2. (20 + 15) = 70 u.do.

Rešitev b

Diagram zagotavlja višino h = 12 u.A, zato je območje mogoče izračunati s formulo:

A = a x h

A = 20 x 12 u.do.² = 240 u.do.²

Ne glede na izbrano enoto za merjenje strani in višine je območje vedno izraženo v kvadratnih enotah.

Enak rezultat, če dobite pri izračunu območja z drugo višino romboida, ki je vredna 16 u.do. Prav zares:

A = 16 x 15 u.do.² = 240 u.do.²

Rešitev c

Kot α je mogoče izračunati skozi:

Lahko vam služi: položaj, osrednja težnja in disperzija

h = b. greh α

Ker so vrednosti H in B znane, torej:

α = arcsen (h/b) = arcsen (12/15) = 53.13

Če se spomnimo, da sta kota α in β dopolnila, je izpolnjen:

α + β = 180 ° ⇒ β = 180 - 53.13. = 126.87 °

Rešitev d

Dolžina segmenta RX je enostavno izračunati, ker je dovolj informacij, da ga najdete. Na primer skozi:

Rx = rv . cos α = 15 . Cos 53.13. u.do. = 9 u.do.

Tudi skozi teorem pitagore skozi pravokotni trikotnik strani 15 in 12 u.na:

(RV)² = (Rx)² + h²

Odstranjevanje dolžine interesnega segmenta:

Rx = √ [(rv)² - h²] = √ [15² - 12²] = √81 = 9

Rešitev e

Ukrep ene od diagonalov, na primer diagonala, ki se pridruži vrhovi R in T, ki je glavna diagonala, daje kosinski teorem, kot je bilo že razloženo, zato tam nadomestimo vrednosti:

D_M = √ (20² + 25² - 2. dvajset. petnajst .Cos 126.87 °) = 37.22 u.do.

Za manjšo diagonalo:

D_m = √ (20² + 25² - 2. dvajset. petnajst .Cos 53.13.) = 25.79 u.do.

Reference

1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
2. Baldor, a. 1973. Geometrija in trigonometrija. Srednjeameriški kulturni uvodnik.
3. In. Do. 2003. Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
4. Jiménez, r. 2010. Matematika II. Geometrija in trigonometrija. Druga izdaja. Dvorana Prentice.
5. Redni poligoni. Okreval od: Mate.inženiring.USAC.Edu.Gt.
6. Formule vesolja. Rhomboid. Okrevano od: univerzeformulas.com.
7. Wikipedija. Rhomboid. Okrevano od: je.Wikipedija.org.