Popoln kvadratni trinomial

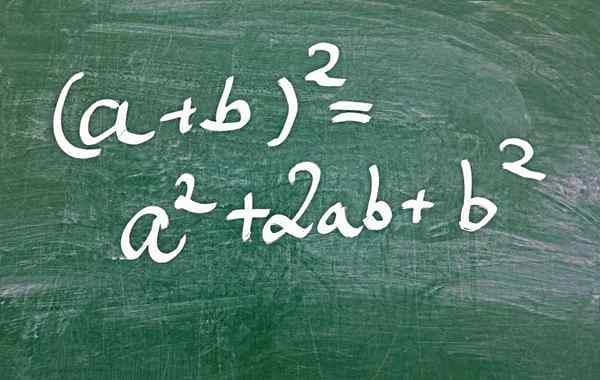Slika 1.- Eden od načinov za pridobitev popolnega kvadratnega trinoma je skozi kvadrat vsote

Kaj je popoln kvadratni trinomial?

Popoln kvadratni trinomial je, da je polinom treh izrazov, od katerih sta dva popolna kvadrata količin A in B in pred njimi enaki znak, tretji izraz pa je točno dvojni produkt A in B drugačen znak.

Popoln kvadratni trinomial dobimo s kvadratom vsote ali razlike binomne in algebraično, njegova oblika je naslednja:

do² ± 2 ∙ AB + B²

Kot je razvidno, popoln kvadratni trinomial vsebuje:

• Dva neimenovana kvadratna izraza pred istim znakom: a² in b²
• Tretji izraz 2 ∙ AB, ki je dvojni produkt kvadratnih korenin kvadratnih izrazov in pred njimi je mogoče pozitiven ali negativni znak.

Popolni kvadratni trinomiji so lahko ena ali več spremenljivk. Na primer, naslednji trinomial je popoln kvadrat spremenljivke:

• x² + 6x + 9

Upoštevajte, da prvi izrazi (x²) in tretji (9) so kvadratni od zneskov, imenovanih A in B. Res, x² To je kvadrat x in 9 je kvadrat 3. Na ta način lahko napišete naslednje:

a = x

B = 3

In preostali izraz je dvojni produkt X in 3:

6x = 2 ∙ 3 ​​∙ x

Ko je preverjanje izvedeno, je gotovo, da je ta trinomial popoln kvadrat.

Primeri

Slika 2.- Primeri popolnih kvadratnih trinomij. Vir: f. Zapata.

Popolni kvadratni trinomiji se pojavljajo tudi v dveh ali več spremenljivkah, na primer:

4x² + 4xy + in²

To je trinomial v dveh spremenljivkah: "x" in "y". Lahko je zagotovljeno, da gre za popoln kvadratni trinomial, saj predstavlja dva kvadratna izraza:

4x² = (2x)²

in² = (y)²

In preostali izraz je dvojni produkt ustreznih kvadratnih korenin: "2x" in "y":

Vam lahko služi: Orthoedro: formule, območje, prostornina, diagonala, primeri

4xy = 2 ∙ 2x ∙ in

Do zdaj predstavljene trinomije so 2. razred v spremenljivki "x", vendar jim ni nujno, da so takšni. Naslednji trinomial je 4. razred v "x":

9x⁴ - 30x²YZ + 25y²z²

Zlahka je preverjena, da je to popoln kvadratni trinomial. Prvi izraz je popoln 3x kvadrat², Od (3x²)² = 9x⁴.

Izraz 25y²z² je enak (5yz)². Končno je preostali izraz 2 ∙ 3x²∙ 5yz = 30 x²in z.

Po drugi strani pa spodaj prikazani trinomiji niso popolni kvadratni trinomiji:

• x²  + 8x - 16

Ni popoln kvadratni trinomial, ker je 16, čeprav je 4², Pred njim je negativni znak, drugi kvadratni izraz (x²) je pozitivno.

• x²  - 15x + 25

Prav tako ni popoln kvadratni trinomial, ker čeprav ima dva kvadratna izraza: x² in 5², Izraz 15x ni enak 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Ta trinomial ni popoln kvadrat, saj vsebuje le kvadratni izraz: 4x² = (2x)².

Kvadrat vsote in kvadrat razlike

Popolne kvadratne trinomije dobimo z razvojem dveh vrst pomembnih izdelkov:

• Kvadrat vsote.
• Kvadrat razlike.

Najprej je razvoj pridobljen iz distribucijske lastnosti, saj dvig kvadratnih binomnih sredstev pomnoži s samim seboj:

(A ± b)² = (a ± b) × (a ± b) = a² ± a ∙ b ± b ∙ a + b² = a² ± 2a ∙ B + B²

Pridobljen trinomija je rezultat, ki si ga zapomni le malo prakse in je nekakšna bližnjica, ki olajša razvoj, zato se imenuje izjemen izdelek.

Vam lahko služi: transcendentne številke: kaj so, formule, primeri, vaje

Naslednje trinomije zlahka pridobijo z znanim izdelkom, ne da bi ponovno uporabili distribucijsko lastnost.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 in² +20xy + 4x²

Faktorizacija popolnega kvadratnega trinoma

Pogosta in potrebna operacija v algebri je faktorizacija popolnega kvadratnega trinomiala, s pomočjo katerega se trinomial izraža kot kvadrat vsote ali odštevanje dveh izrazov (binom).

Za razvoj opaznega izdelka je obratno delovanje, saj ima nastali trinomial ideja, da dobite binom, ki ga povzroči, ko se dvigne na 2.

Na primer, v predhodno analizirani 4x Perfect Square Trinomial² + 4xy + in², Kaj je binoma, da vas, ko je na kvadrat?

Ustrezne kvadratne korenine kvadratnih izrazov so:

√ (4x²) = 2x

Kar je enakovredno: 4x² = (2x)²

√ (in²) = y

Enakovredno temu: in² = (y)²

Zato:

4x² + 4xy + in² = (2x + y)²

In kaj je binom, ki izvira iz popolnega kvadratnega trinomiala 9x⁴ - 30x²YZ + 25y²z²? Spet se izvlečejo kvadratne korenine kvadratnih izrazov:

√ (9x⁴) = 3x²

√ (25 in²z²) = 5yz

Tako:

(3x² - 5yz)² = 9x⁴ - 30x²YZ + 25y²z²

Rešene vaje

Vaja 1

V vsakem od naslednjih trinomij dokončajte prazno z izrazom, ki mu manjka popoln kvadratni trinomial:

a) m² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Rešitev

V skladu s formulo pomembnega izdelka:

Vam lahko služi: komplementarni koti: Kateri in kako se izračunajo, primeri, vaje

(A ± b)² = A² ± 2a ∙ B + B²

Trinomiala:

m² + 18m + _____

Sledi, da:

a = m (tako da² = m²)

Poleg tega je osrednji izraz: 2 ∙ a ∙ b = 2m ∙ b = 18m, torej b = 9 in njen kvadrat je 9² = 81. Trinomial je po formuli pomembnega izdelka takšen:

(M + 9)² = M² + 18m + 81

• Rešitev b

V tem trinomialu:

4x² - _____ + 64

Lahko veste in B:

A = √ (4x²) = 2x

B = √64 = 8

Zato je manjkajoči izraz dvojni produkt A in B:

2 ∙ AB = 2 ∙ 8 ∙ 2x = 32x

In iskani trinomial je:

4x² - 32x + 64

• Rešitev c

V trinomialu:

_____ + 30n + 25

Prvi izraz manjka, vendar je znano, da:

B = √25 = 5

In

2 ∙ AB = 2 ∙ a ∙ 5 = 10a = 30n

Zato je a = 3n in iskani trinomial je:

9n² + 30n + 25

Vaja 2

Preverite, ali je naslednji popoln kvadratni trinomial in ga upoštevajte:

16y² - 24yz + 9z²

• Rešitev

Najprej je dokazano, da so pred kvadratnimi izrazi istega znaka in nato najdejo ustrezne kvadratne korenine:

A = √ (16y²) = 4y

B = √ (9z²) = 3z

Potem morate preveriti, ali je preostali izraz dvojni produkt A in B:

2 ∙ AB = 2 ∙ 4y ∙ 3z = 24yz

Če je, potem je lahko trinomial dejavnik kot kvadrat razlike, saj je osrednji izraz pred negativnim znakom:

16y² - 24yz + 9z² = (4y - 3z)²

Reference

1. Jiménez, r. 2008. Algebra. Dvorana Prentice.
2. Kateine ​​matematične lekcije. Popolni kvadratni trinomiji. Okreval od: Katesmathlessons.com.
3. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
4. Zill, d. 2008. Predhod z napredkom izračuna. 4. Izdaja. McGraw Hill.