Trikotnik izosceles

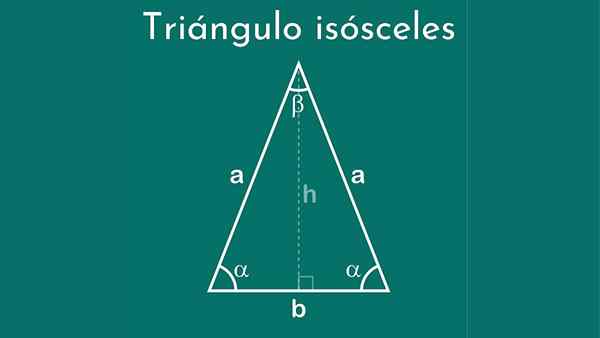
Trikotnik izosceles ima dve enaki strani in eno drugačno

Kaj je izosceles trikotnik?

A Trikotnik izosceles Gre. Ta zadnja stran se imenuje baza. Zaradi te značilnosti je bilo to ime, kar v grščini pomeni "enake noge".

Trikotniki so poligoni, ki se v geometriji štejejo za najpreprostejše, saj jih tvorijo tri strani, trije koti in tri točke. Oni so tisti, ki imajo v primerjavi z drugimi poligoni najmanj število strani in kotov, vendar je njihova uporaba zelo obsežna.

Značilnosti trikotnikov izoscele

Trikotnik Isosceles je bil z mero stranskih strani razvrščen kot parameter, saj sta dve strani skladni, torej imata enako dolžino.

Glede na amplitudo notranjih kotov so trikotniki izosceles razvrščeni kot:

• Trikotnik pravokotnika iz izoscele: Dve strani sta enaki. Eden od njegovih kotov je naravnost (90^tudi) In ostali so enaki (45^tudi vsak)
• Isosceles obtuse trikotnik: Dve strani sta enaki. Eden od njegovih kotov je obljuden (> 90^tudi).
• Trikotnik izosceles acutangle: Dve strani sta enaki. Vsi njegovi koti so akutni (< 90^tudi), Kjer imata dva enak ukrep.

Komponente

• Mediana: To je črta, ki na eni strani pušča od sredine točke in doseže nasprotno vrhovo. Trije mediji se udeležujejo na točki, imenovani Baricentro ali Centroid.
• Bisektor: To je polčas, ki razdeli kot vsake točke na dva kota enakega merila. Zato je znana kot simetrična os, ta vrsta trikotnikov.
• Mediatrix: Je segment, pravokoten na stran trikotnika, ki izvira iz sredine tega. V trikotniku so tri mediatike in se udeležujejo točke, imenovane Pococentro.
• Višina: To je črta, ki sega od vrha do strani, ki je nasprotna in tudi ta črta je pravokotna na to stran. Vsi trikotniki imajo tri višine, ki sovpadajo v točki, imenovani Ortocenter.

Isosceles Triangles lastnosti

Trikotniki Isosceles so definirani ali identificirani, ker imajo več lastnosti, ki jih predstavljajo, izvirajo iz teoremov, ki jih predlagajo veliki matematiki:

Notranji koti

Vsota notranjih kotov je vedno enaka 180^tudi.

Vsota strani

Vsota ukrepov dveh strani mora biti vedno večja od ukrepa tretje strani, A + B> C.

Skladne strani

Trikotniki izosceles imajo dve strani z enakim ukrepom ali dolžino; to pomeni, da so skladni in tretja stran se razlikuje od teh.

Skladni koti

Isosceles Triangles so znani tudi kot izoangulozni trikotniki, saj imajo dva zorna kota, ki imata enak ukrep (skladen). Te se nahajajo na dnu trikotnika, ki nasprotujejo straneh, ki imajo enako dolžino.

Vam lahko služi: trapezna prizma

Zaradi tega, teorema, ki to vzpostavlja:

"Če ima trikotnik dve skladni strani, bodo koti, ki nasprotujejo tem strani, tudi skladni.". Če je trikotnik izosceles, so koti njegovih baz skladni.

Primer:

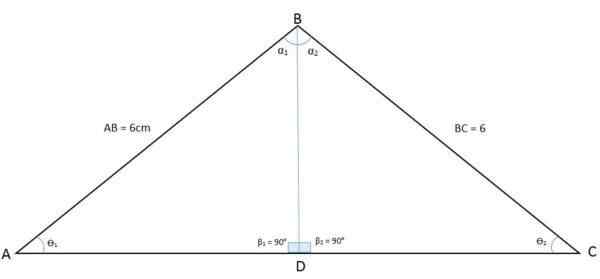
Na naslednji sliki opazimo trikotnik ABC. Pri risanju svojega bisektorja z vrha kota B do podstavka je trikotnik razdeljen na dva trikotnika BDA in BDC:

Bisektor, ki se deli na dva trikotnika, enaka izosceles trikotniku

Na ta način je bil kot vrha B razdeljen tudi na dva enaka kota. Bisektor je zdaj skupna stran (BD) med tema dvema novima trikotnikoma, medtem ko sta strani AB in BC kongruentne strani. To je primer stranske, kota, strani (LAL).

To kaže, da imata kota vrhov A in C enak ukrep, poleg tega pa je mogoče dokazati, da sta trikotniki BDA in BDC skladni, tudi AD in DC strani sta tudi AD in DC.

Višina, mediana, mediatrix in bisektor so naključni

Črta, narisana od vrha, nasproti podstavka do sredine točke trikotnika izosceles, je hkrati višina, mediana in mediatrix, pa tudi bisektor glede na nasprotni kot podstavka.

Vsi ti segmenti sovpadajo v tistem, ki jih predstavlja.

Primer:

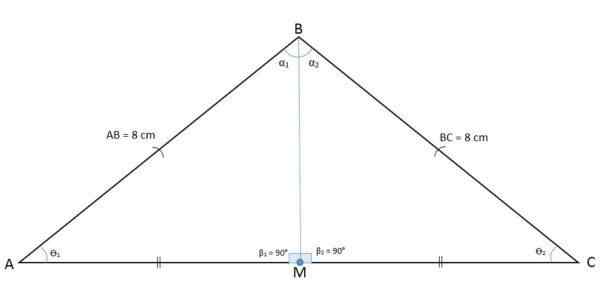
Na naslednji sliki opazimo trikotnik ABC s srednjo m točko, ki deli bazo na dva segmenta BM in CM.

Višina, mediana, mediatrix in bisektor so naključni

Pri risanju segmenta od točke M do nasprotne točke po definiciji dobimo mediana AM, kar je glede na tono in na stran BC.

Ker segment AM deli trikotnik ABC na dva enaka trikotnika AMB in AMC, to pomeni, da bo primer stranskega, kota, strani in zato AM tudi bisektor Bâc.

Zato bo bisektor vedno enak srednji in obratno.

Segment AM tvori kote, ki imajo enak ukrep za trikotnike AMB in AMC; to pomeni, da so dodatni, tako da bo ukrep vsakega:

Med. (Amb) + Med. (AMC) = 180^tudi

2 _* Med. (AMC) = 180^tudi

Med. (AMC) = 180^tudi ÷ 2

Med. (AMC) = 90^tudi

Znano je, da so koti, ki jih tvori segment AM glede osnove trikotnika.

Zato predstavlja višino in mediatrix, saj ve, da je m sredi točke.

Zato črta AM:

• Predstavlja višino BC.
• Je srednje velikosti.
• Vsebuje v BC Mediatrix.
• To je bisektor vrhovnega kota

Relativne višine

Tudi višine, ki so glede na enake strani.

Vam lahko služi: popolne številke: kako jih prepoznati in primere

Ker ima trikotnik izosceles dve enaki strani, bosta tudi dve višini enaki.

Orocentro, Baricentro, Interes in Colecentro Coinsides

Ker so višina, mediana, bisektor in mediatrik, povezana z osnovo, hkrati predstavljena z istim segmentom, bodo ortocenter, baricentro, inwarter in obkrožili kolinealne točke, torej jih bomo našli v isti vrstici:

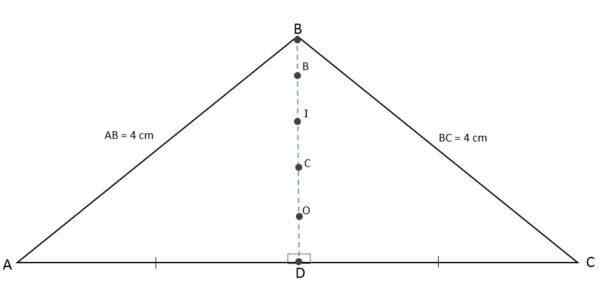Ortocenter, Baricentro, Inwertintro in OCCENTRO so prav tako naključni

Izračun trikotnikov izosceles

Kako izračunati obod?

Obod poligona se izračuna v vsoti strani.

Kot v tem primeru ima trikotnik izosceles dve strani z istim ukrepom, se njegov obod izračuna z naslednjo formulo:

P = 2_*(stran a) + (stran b).

Kako izračunati višino?

Višina je črta, pravokotna na podlago, trikotnik deli na dva dela, enaka, tako da sega na nasprotno vrhovo.

Višina predstavlja nasprotni kateto (a), polovico podstavka (b/2) do sosednjega kateta in stran "A" predstavlja hipotenuzo.

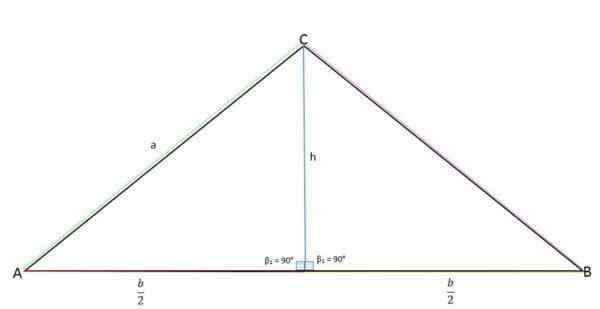Izračun višine trikotnika izoscele

Z uporabo teorema pitagore lahko določimo vrednost višine:

do² + b² = c²

Kje:

do² = višina (h).

b² = B / 2.

c² = stran a.

Zamenjava teh vrednosti v teoremu pitagore in čiščenje višine, ki jo imate:

h² + (b / 2)² = do²

h² + b² / 4 = do²

h² = do² - b² / 4

H = √ (do² - b² / 4).

Če je znan kot, ki ga tvorijo kongruentne strani, lahko višino izračunamo z naslednjo formulo:

Kako izračunati območje?

Trikotniki se vedno izračunajo z isto formulo, pomnožijo bazo po višini in delijo z 2:

Obstajajo primeri, ko so znani le ukrepi dveh strani trikotnika in med njimi oblikovani kot. V tem primeru je za določitev območja potrebno uporabiti trigonometrične razloge:

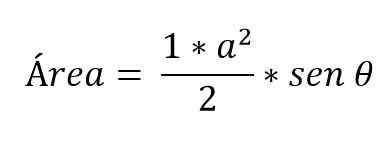
Kako izračunati bazo trikotnika?

Ker ima trikotnik izosceles dve enaki strani, je za določitev vrednosti svoje osnove treba vedeti vsaj merilo višine ali enega od njegovih kotov.

Če poznate višino, se uporablja teorem Pythagoras:

do² + b² = c²

Kje:

do² = višina (h).

c² = stran a.

b² = B / 2, ni znano.

Počistimo b² formule in moramo:

b² = a² - c²

B = √ a² - c²

Ker ta vrednost ustreza polovici baze, jo je treba pomnožiti z 2, da dobimo celotno mero baze trikotnika izosceles:

b = 2 _* (√ a² - c²)

V primeru, da je znana le vrednost njegovih enakih strani in kota med njima, se uporablja trigonometrija, ki črpa črto od vrha do podstavka, ki isosceles trikotnik deli na dva pravokotnika trikotnika.

Na ta način se izračuna polovica baze z:

Znana je tudi vrednost višine in kot, ki nasprotuje bazi. V tem primeru lahko s trigonometrijo določimo osnovo:

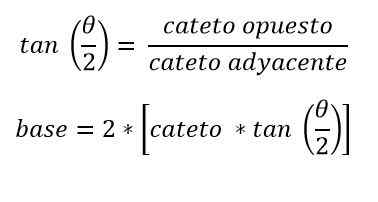
Vaje

Prva vaja

Poiščite območje Triangle Isosceles ABC, vedoč, da dve njeni strani merita 10 cm in tretja stran meri 12 cm.

Lahko vam služi: antiderivativ: formule in enačbe, primeri, vaje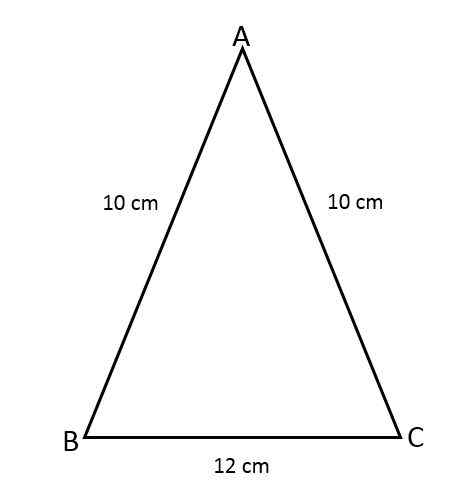

Rešitev

Za iskanje območja trikotnika je potrebno.

Na voljo so naslednji podatki o trikotniku Isosceles:

• Enake strani (a) = 10 cm.
• Osnova (b) = 12 cm.

Vrednosti se nadomestijo v formuli:

Druga vaja

Dolžina obeh enakih strani trikotnika izosceles meri 42 cm, združitev teh strani tvori kot 130^tudi. Določite vrednost tretje strani, območje tega trikotnika in oboda.

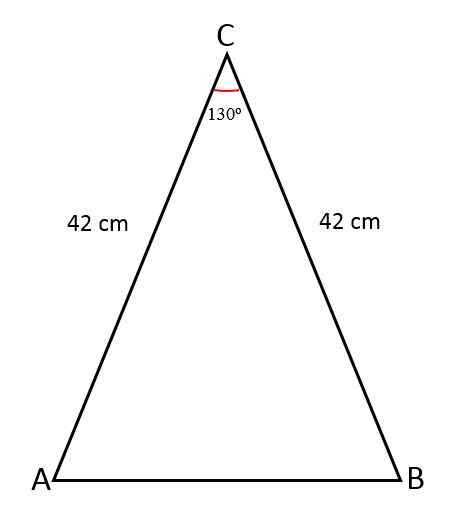
Rešitev

V tem primeru so med njimi znani ukrepi strani in kot.

Če želite vedeti vrednost manjkajoče strani, to je osnova tega trikotnika, je črta, pravokotna nanj.

• Enake strani (a) = 42 cm.
• Kot (ɵ) = 130^tudi

Zdaj se s trigonometrijo izračuna vrednost polovice osnove, kar ustreza polovici hipotenuze:

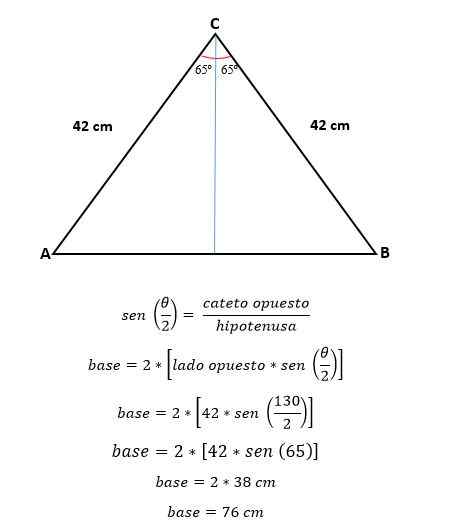
Če želite izračunati območje.

S trigonometrijo bo:

Obod se izračuna:

P = 2_*(stran a) + (stran b).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Tretja vaja

Izračunajte notranje kote izosceles trikotnika, vedoč, da je osnovni kot â = 55^tudi

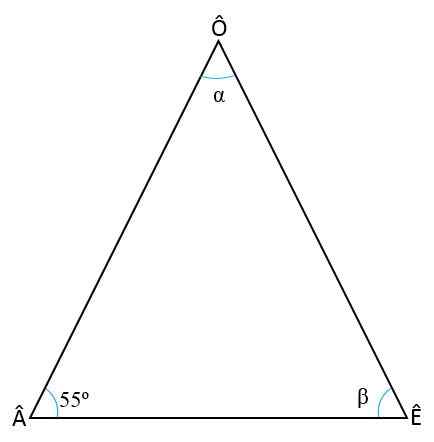
Rešitev

Za iskanje dveh manjkajočih kotov (ê in ô) se je treba spomniti dveh lastnosti trikotnikov:

• Vsota notranjih kotov vsakega trikotnika bo vedno = 180^tudi:

 + ê + ô = 180 ^tudi

• V izosceles trikotniku so koti baze vedno skladni, torej imajo isti ukrep:

 = ô

Ê = 55^tudi

Za določitev vrednosti kota ê se nadomestijo vrednosti drugih kotov v prvem pravilu in ê očisti:

55^tudi + 55^tudi + Ô = 180 ^tudi

110 ^tudi + Ô = 180 ^tudi

Ô = 180 ^tudi - 110 ^tudi

Ô = 70 ^tudi.

Reference

1. Álvarez, npr. (2003). Geometrijski elementi: s številnimi vajami in geometrijo kompasa. Univerza v Medellinu.
2. Álvaro Rendón,. R. (2004). Tehnična risba: zvezek z dejavnostjo.
3. Angel, a. R. (2007). Elementarna algebra. Pearson Education.
4. Arthur Goodman, L. H. (devetnajst devetdeset šest). Algebra in trigonometrija z analitično geometrijo. Pearson Education.
5. Baldor, a. (1941). Algebra. Havana: Kultura.
6. José Jiménez, L. J. (2006). Matematika 2.
7. Tuma, J. (1998). Priročnik za inženirstvo matematike. Wolfram Mathworld.